数值分析
帕德逼近 (Padé approximation)
引言 Padé 逼近多项式 \(R_{n
数学基础
From Cartesian to polar (从笛卡尔坐标到极坐标)
本文档提供了从笛卡尔坐标转换为极坐标的简单介绍。转换过程包括使用勾股定理计算到原点的距离，以及使用反正切函数并进行适当的象限调整来确定角度。主要内容包括基本转换公式、处理坐标轴上的特殊情况，以及在编程语言中使用atan2函数的实际实现。示例演示了不同象限中点的转换过程。
数值方法
A note on Gudi’s analysis of the IPDG method
In this note, we give an alternative proof for an estimate in Gudi’s method, where the author uses a result in a posteriori result without proof.
科普读物
为什么艾伦·图灵 (Alan Turing) 说科学是一个微分方程而宗教是一个边界条件?
图灵说过一句话: science is a differential equation and religion is a boundary condition. 翻译过来就是: 科学是一个微分方程而宗教是一个边界条件. 这里的宗教我们大概可以替理解成国人的信仰. 对这句话理解一些人有一些非常独到的理解, 也许会对从事科学研究的人有某些启发.
Python 科学计算: SymPy
Python 因为开源免费, 语法简洁和第三方库众多等优点成为近年来的最流行的编程语言之一. 本文的主要目标是给出一些常用的符号计算示例和代码, 内容涉及数学分析的各个主题, 用来快速入门 Python 最常用的符号计算库 — Sympy.
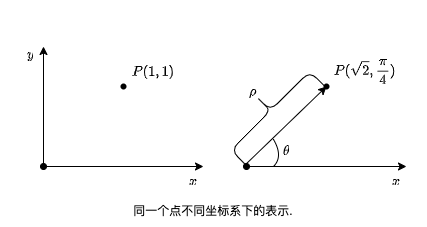
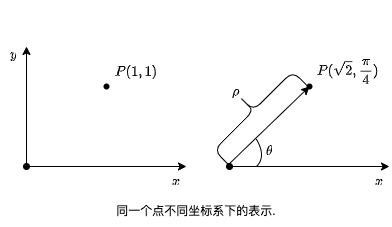
Read moreFrom Cartesian to polar (从笛卡尔坐标到极坐标)
本文档提供了从笛卡尔坐标转换为极坐标的简单介绍。转换过程包括使用勾股定理计算到原点的距离，以及使用反正切函数并进行适当的象限调整来确定角度。主要内容包括基本转换公式、处理坐标轴上的特殊情况，以及在编程语言中使用atan2函数的实际实现。示例演示了不同象限中点的转换过程。
Read moreA note on Gudi’s analysis of the IPDG method
In this note, we give an alternative proof for an estimate in Gudi’s method, where the author uses a result in a posteriori result without proof.
Read more参数曲线和极坐标曲线动态绘图
参数方程和极坐标方程曲线的动态绘制程序, python 实现
Read more
极坐标下平面图形的面积
极坐标曲线 直角坐标系下, 平面图形中的
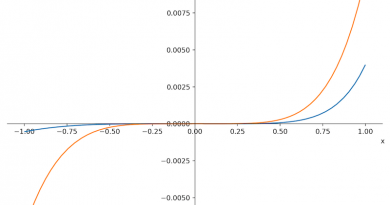
Read more
牛顿和莱布尼茨的导数
我们想要梳理一下导数发展最初的萌芽概念,
Read more
Well-posedness of IVPs
This is a study note
Read moreA short introduction to Matrix exponentials
我们将讨论矩阵指数函数的定义和基本性质. This is a short introduction to Matrix exponentials.
Read more
Allen-Cahn 方程的物理背景和推导过程
相场方法是一种基于热力学的方法, 最常用于模拟材料中的相变和不断演化的微观结构. 这是一种介观方法, 其中的变量可以是抽象的非守恒量, 用于测量系统是否处于给定的相中 (如固态、液态等), 也可以是守恒量, 如浓度. 界面由这些量从一个相到另一个相的平滑变化来描述, 并且是扩散的, 而不是尖锐的.
Read more