线性系统的迭代求解: 为什么需要预处理?

2021年11月29日2021年12月12日 numanal 0 个评论条件数, 线性系统, 预处理

预备知识

线性系统迭代求解的基础方法
MATLAB 基础编程

本文中涉及的理论部分可以在通用的数值线性代数参考书目中找到, 具体可以参考: 数值分析教材推荐.

问题表述

考虑如下的线性系统\[ Ax = b,\tag{1}\]其中系数矩阵 $A \in \mathbb{R}^{n\times n}$ 对称正定, 右端项 $b \in \mathbb{R}^{n}$. 最经典的方法为共轭梯度 (CG) 方法, 其迭代序列满足:\[ \|x-x^{(k)}\|_{A} \leq 2 \left( \frac{\sqrt{\kappa_{2}(A)}-1}{\sqrt{\kappa_{2}(A)}+1} \right)^{k} \|x-x^{(0)}\|_{A}, \tag{2}\]其中 $\kappa_{2}(A)$ 表示矩阵 $A$ 的谱条件数. 当 $A$ 是坏条件时, 即 $\kappa_{2}(A)$ 很大, CG 方法的收敛较慢.

解决方法. 选取合适的预处理子 $P$, 使 $\kappa_{2}(P^{-1}A) \ll \kappa_{2}(A)$, 得到预处理共轭梯度 (PCG) 方法, 其迭代序列满足:\[ \|x-x^{(k)}\|_{\widetilde{A}} \leq 2 \left( \frac{\sqrt{\kappa_{2}(P^{-1} A)}-1}{\sqrt{\kappa_{2}(P^{-1} A)}+1} \right)^{k} \|x-x^{(0)}\|_{\widetilde{A}}, \tag{3}\]其中 $P = L L^{T}$, $\widetilde{A} = L^{-1} A L^{-T}$.

预处理子

预处理子的选取原则

以预处理子 $P$ 为系数矩阵的线性系统容易求解;
预处理子 $P$ 尽量接近参数矩阵 $A$.

上述两个条件是互相矛盾的, 所以在选取预处理子时, 应平衡这两个条件.

预处理的三种方式:

左预处理 $P^{-1} A x = P^{-1} b;$
中心预处理 $P = LU; \enspace L^{-1}AU^{-1}y = L^{-1} b; \enspace x = U^{-1}y,$
右预处理 $AP^{-1}y = b; \enspace x = P^{-1}y.$

三种预处理方式的特点:

左预处理最自然, 不需要额外去计算 $x$;
中心预处理可以保留系统的对称性: 当 $A$ 对称时, 预处理子应选取对称矩阵 $P = L L^{T}$;
右预处理不影响残差: 原来的残差 $r = b – Ax$, 预处理后的残差 $r = b – AP^{-1}y$.

基础预处理子

对角预处理子 (Jocobi 预处理子): $P = \mathrm{diag}(A);$
三对角预处理子: $P=\mathrm{tridiag}(A);$
Gauss-Seidel 预处理子: $P = D + L,$ 其中 $D=\mathrm{diag}(A)$, $L$ 为矩阵 $A$ 的严格下三角部分;
SOR 预处理子: $P = \frac{1}{\omega}(D+\omega L),$ 其中 $\omega$ 为松弛参数.
不完全 LU (ilu) 分解预处理子: $A \approx LU$, 其中 $L,U$ 分别为下三角和上三角矩阵, 且保持稀疏性. MATLAB 代码为

[L,U] = ilu(A,setup);
x = gmres(A,b,restart,tol,maxit,L,U).

不完全 Cholesky (ichol) 分解预处理子 (要求系数矩阵 A 对称): $A \approx LL^{T},$ 其中 $L$ 为下三角矩阵, 且保持稀疏性. MATLAB 代码为

L = ichol(A,opts);
x = pcg(A,b,tol,maxit,L,L^{T}).

数值结果

本节我们利用一个简单的数值算例来说明预处理的效果. 考虑如下泊松方程\[\begin{equation}\begin{split} – \Delta \mathbf{u} + q \nabla\cdot \mathbf{u} &= f \quad \text{in} \enspace \Omega,\\ \mathbf{u} &= g \quad \text{on} \enspace \partial\Omega.\end{split}\end{equation} \tag{3}\]通过有限差分方法离散, 可以得到一个对称正定的线性系统 $Ax = b$, 其中$$\begin{equation*}\begin{split} A &= \frac{1}{h^2}(I \otimes K + K \otimes I) + \frac{q}{2 h}(I \otimes T + T \otimes I) \in \mathbb{R}^{n \times n},\\ K &= \mathrm{tridiag}(-1,2,-1) \in \mathbb{R}^{l \times l}, \\ T &= \mathrm{tridiag}(-1,0,-1) \in \mathbb{R}^{l \times l},\\ h &= 1/l, \ q = 10.\end{split}\end{equation*}$$ 生成上述线性系统的代码为

l = 40;
h = 1/l;
q = 10;
K_1 = gallery('tridiag',l,-1,2,-1);
K_2 = gallery('tridiag',l,-1,0,1);
A =(1/h^2)*(kron(speye(l),K_1)+kron(K_1,speye(l)))+ ...
    q/(2*h)*(kron(speye(l),K_2)+kron(K_2,speye(l)));

我们知道, 迭代方法的收敛速度与线性系统的谱条件数是紧密相关的. 以预处理的 Gmres 方法为例, 理论上可以证明线性系统的条件数越小收敛速度越快. 对于椭圆问题的差分离散系统 $A$, 理论上它的条件数是一个病态的发展过程, 增长速度大概为 $O(h^{-2})$; 即当网格步长减小一半, 条件数变成原来的 4 倍. 这是一个极其值得注意的过程, 因为一般情况下我们必须通过加细网格来提高数值方程的求解精度, 但是这会导致离散出来的线性系统规模更大, 条件数更大. 当系统的规模或条件数达到一定程度, 没有预处理的 Gmres 方法是无法在一定迭代步数或时间范围内收敛的, 因此必须借助合适的预处理子来加速收敛过程.

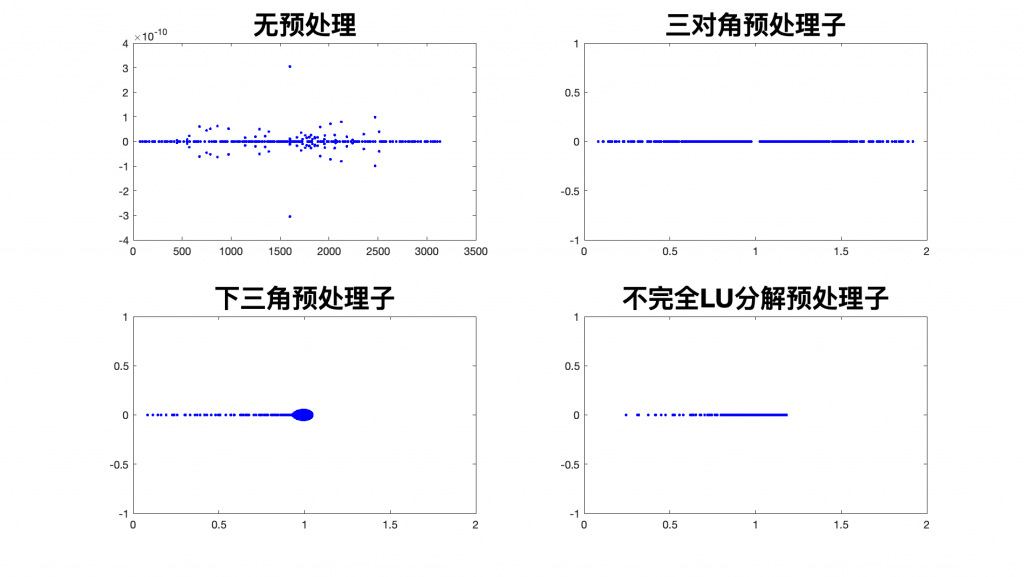
首先, 我们考察常用的预处理子对条件数的影响, MATLAB 代码见附录. 图 1, 2 中分别给出了当 $l=20, 40$ 时线性系统的特征值分布情况. 可以看出在没有预处理时, 线性系统最大的特征值大概增长了四倍, 符合理论预期. 另外, 三个常用的预处理子均可以缩小特征值的分布范围 (相应的减小谱条件数), 其中不完全的 LU 分解效果最好. 这里我们需要注意的是一般简单的预处理矩阵数值实现相对容易但是效果相对较差, 复杂的预处理子数值实现相对困难但是效果相对较好; 因此, 实际情况中需要对两者进行一个考量, 有所取舍.

其次, 我们考察常用的预处理子真实的数值效果, MATLAB 代码见附录. 图 3, 4 分别给出了当 $l=20, 40$ 时 Gmres 方法的收敛过程. 从中可以看出, 三个常用的预处理矩阵均可以达到加速收敛的效果. 但是, 当问题的规模变大以后, 需要更多的迭代步数来达到要求的数值精度. 这也是处理病态问题时需要解决的重要问题之一, 即如何寻找一个预处理子使它的加速效果不随问题的规模增大而减弱? 有兴趣的读者可以查找相关的文献来学习.

线性系统的迭代求解通常会随问题的规模增大而变得异常困难, 合适的预处理子可以大幅加速迭代求解过程, 进而减小问题求解的消耗成本. — 图 4.

附录

条件数代码

clear;
% 
% 生成线性系统
% 
l = 20;
h = 1/l;
q = 10;
K_1 = gallery('tridiag',l,-1,2,-1);
K_2 = gallery('tridiag',l,-1,0,1);
A =(1/h^2)*(kron(speye(l),K_1)+kron(K_1,speye(l)))+ ...
    q/(2*h)*(kron(speye(l),K_2)+kron(K_2,speye(l)));
b = ones(size(A,1),1);
% 
% 三对角预处理子
P1 = A-tril(A,-2)-triu(A,2); 
% 下三角预处理子
P2 = tril(A,0);
% 不完全LU分解预处理子
setup.type = 'nofill'; 
setup.droptol = 0.1; 
[L,U] = ilu(A,setup); 
P3 = L*U;
% 
% 停机准则和迭代过程
% 
tol=1e-7;
for k0 = 1:100
    [x,flag,res0(k0)] = gmres(A,b,[],tol,k0);
    if res0(k0) < tol
        break 
    end
end
for k1 = 1:100
    [x,flag,res1(k1)] = gmres(A,b,[],tol,k1,P1); 
    if res1(k1) < tol
        break
    end
end
for k2 = 1:100
    [x,flag,res2(k2)] = gmres(A,b,[],tol,k2,P2);
    if res2(k2) < tol
        break
    end
end
for k3 = 1:100
    [x,flag,res3(k3)] = gmres(A,b,[],tol,k3,P3);
    if res3(k3) < tol
        break
    end
end
% 
% 收敛过程绘图
% 
semilogy(1:size(res0,2),res0,'k-','LineWidth',1.5); 
hold on;
semilogy(1:k1,res1,'mo-'); 
semilogy(1:k2,res2,'g+-'); 
semilogy(1:k3,res3,'b*-');
title('Preconditioned GMRES method','Interpreter','latex','Fontsize',32);
xlabel('Number of iterations','Fontsize',26);
ylabel('Relative errors','Fontsize',26);
legend('NON','P_{tridiag}','P_{tril}','P_{ilu}');

预处理效果代码

% 常用预处理子的效果试验
% 
% 生成线性系统
% 
l = 20;
h = 1/l;
q = 10;
K_1 = gallery('tridiag',l,-1,2,-1);
K_2 = gallery('tridiag',l,-1,0,1);
A =(1/h^2)*(kron(speye(l),K_1)+kron(K_1,speye(l)))+ ...
    q/(2*h)*(kron(speye(l),K_2)+kron(K_2,speye(l)));
% 
% 三对角预处理子
P1 = A-tril(A,-2)-triu(A,2); 
% 下三角预处理子
P2 = tril(A,0);
% 不完全LU分解预处理子
setup.type = 'nofill'; 
setup.droptol = 0.1; 
[L,U] = ilu(A,setup); 
P3 = L*U;
% 
% 线性系统特征值绘图
% 
eigA = eig(full(A)); 
F1 = plot(real(eigA),imag(eigA),'b.');
title('无预处理','Interpreter','latex','Fontsize',24); 
xlabel('real','Fontsize',26); 
ylabel('imaginary','Fontsize',26);
eig2 = eig(full(P1\A)); 
F2 = plot(real(eig2),imag(eig2),'b.'); 
title('三对角预处理子','Interpreter','latex','Fontsize',24); 
axis([0 2 -1 1])
eig3 = eig(full(P2\A)); 
F3 = plot(real(eig3),imag(eig3),'b.'); 
title('下三角预处理子','Interpreter','latex','Fontsize',24); 
axis([0 2 -1 1])
eig4 = eig(full(P3\A)); 
F4 = plot(real(eig4),imag(eig4),'b.'); 
title('不完全LU分解预处理子','Interpreter','latex','Fontsize',24); 
axis([0 2 -1 1])

分享到: