Allen-Cahn 方程的物理背景和推导过程

基本所有内容来自于 LeSar [1].

简介

相场方法是一种基于热力学的方法, 最常用于模拟材料中的相变和不断演化的微观结构. 这是一种介观方法, 其中的变量可以是抽象的非守恒量, 用于测量系统是否处于给定的相中 (如固态、液态等), 也可以是守恒量, 如浓度. 界面由这些量从一个相到另一个相的平滑变化来描述, 并且是扩散的, 而不是尖锐的.

在相场建模中. 系统的状态由位置和时间的函数来描述, 这种函数一般称为序参数. 序参数可以是非守恒和守恒的, 因此可用于不同的情况.

首先, 我们可以通过考虑参数 \(\phi(\mathbf{r},t)\) 来建立凝固模型, 该参数的值决定了材料的热力学相位. \(\phi=1\) 表示固态, \(\phi=-1\) 表示液态. 在所有热力学系统中, 每个位置上的相（\(\phi\)）都是由系统的自由能决定的. 除了能量之外, 它的值没有任何局部限制. 例如, 假设某一体积的系统是固体. 固体体积转化为液体不需要任何物质的进出, 因此, 除了能量方面的考虑外, 该体积内发生的事情与相邻体积无关. 在这种情况下, 不存在必须遵守的守恒定律, 序参数被称为非守恒. Allen-Cahn 方程的推导基于非守恒序参数的.

其次, 假设 \(C(\mathbf{r},t)\) 表示某种物质在一个点 \(\mathbf{r}\) 的浓度. 要使 \(\mathbf{r}\) 处的浓度增加, 原子必须从材料的其他区域转移到该位置. 因此, 一点浓度的增长需要另一点浓度值的下降. 在 \(\mathbf{r}\) 处的序参数不可能出现无限制的增长, 因为总浓度是守恒的. 控制此类系统行为的方程必须反映守恒量, 而且序参数也必须是守恒的. Chan-Hilliard（CH）方程的推导就是基于守恒的序参数.

假设

对于两相系统, 自由能包括三项:

1. 一种相的能量
2. 另一种相的能量
3. 界面处的能量；

假设 \(f\) 是自由能密度, 它是一个局部函数, 取决于系统在每一点的状态。由于系统的状态由阶参数 \(\phi\)指定，我们可以写成 \(f(\phi(\mathbf{r},t))\)。界面的能量将取决于 \(\phi\)从一个相变到另一个相的速度，所以总能量将是\[ \mathfrak{F}=\int_{\Omega} f^{total}(\phi(\mathbf{r},t),\nabla \phi(\mathbf{r},t))d \mathbf{r}. \tag{2}\]

假设:

• 界面是扩散的;
• (2) 可以关于 \(\nabla \phi\) 泰勒级数展开, 并在二阶项 \((\nabla \phi)^2\) 处截断;
• \(\phi\) 会随着时间的推移而变化, 从而降低自由能;
• \(\phi\) 的动态受热动力支配, 热动力被定义为自由能 \(\mathfrak{F}\) 相对于 \(\phi\) 导数的负值.

一维 AC 方程的推导

相场法假定任何界面都是宽阔、扩散且不尖锐的. 这表明导数 \(\partial \phi/ \partial x\) 被假定为很小, 这意味着我们可以通过用 \(\frac{d\phi}{dx}\) 展开来简化自由能表达, 即消除它的高次. 让 \(g:=\frac{d\phi}{dx}\), 存在围绕 \(g=0\) 的泰勒展开:\[ f^{total}(\phi,g)=f^{total}(\phi,0) + \frac{\partial f^{total}}{\partial g}_{|g=0} g +\frac{1}{2} \frac{\partial^2 f^{total}}{\partial g^2}_{|g=0} g^2 + \cdots \tag{3}\]

• \(f^{总}(\phi,g=0)\) 是平衡态–没有界面, 总能量是两个相的能量总和 \(f(\phi)\);
• 由于界面能量为正, 所以 \(f^{total}(\phi,g=0)\) 一定是最小能量, 因此 \(\frac{\partial f}{\partial g}_{|g=0}=0 \);
• 假设 \(\alpha:=\frac{1}{2}\frac{\partial^2 f}{\partial g^2}_{|g=0}\)恒定. 由于界面能量为正, 所以 \(\alpha>0\) 是成立的.

因此, 忽略高阶项后, 总能量可写成\[ \mathfrak{F}=\int_{\Omega} \left\{ f(\phi) + \frac{\alpha}{2} \left( \frac{\partial \phi}{\partial x} \right)^2 \right\}. \tag{4}\]

自由能包括两个部分, 如 (4) 所示. 第一项是不同相的热力学自由能密度. 第二项是界面处的能量, 其中 \(\alpha\) 是一个常数, 设定了界面的总能量。界面能量与 \(\left(\frac{\partial \phi}{\partial x} \right)^2\) 成正比, 即通过界面的 \(\phi\) 变化斜率的平方. 在这种描述中, 更锐利的界面会导致更高的界面能.

随着时间的推移, 当 \(\mathfrak{F}\) 相对于 \(\phi\) 的导数为零时, 总能量将达到能量最低的状态. 因此, 最小值的条件是\[ 0=\frac{\partial \mathfrak{F}}{\partial \phi} = \frac{\partial f(\phi)}{\partial \phi} -\alpha \frac{\partial^2 \phi}{\partial x^2}. \tag{5}\]上式是所谓的 Euler-Lagrange方程, 它显示了能量 \(\mathfrak{F}\) 达到最小值的必要条件[2].

序参数 \(\phi\) 变化的‘速度’与作用在 \(\phi\) 上的‘力’相关, 类似于原子的速度与作用在原子上的力之间的关系:\[ \frac{\partial \phi}{\partial t} =-L_\phi \frac{\partial \mathfrak{F}}{\partial \phi} =-L_\phi \left[ \frac{\partial f(\phi)}{\partial \phi} -\alpha \frac{\partial^2 \phi}{\partial x^2} \right]. \tag{6}\]等式 (6) 通常被称为梯度下降, 用于寻找自由能的最小值. 它说 \(\phi\) 随时间的变化等于常数 \(L_\phi\) 乘以自由能相对于 \(\phi\) 的函数导数的负数. 当 \(\phi\) 变得稳定时, 它就是 \(\mathfrak{F}\) 的最小值.

AC 方程的能量衰减

假设存在诺伊曼边界条件 \(\frac{\partial \phi}{\partial x}=0\) 或狄里希特条件 \(\phi=0\). 那么, 如下的基本性质成立

\[ \begin{align*} \frac{d}{dt}F(\phi) &= \int_{\Omega}\left[ \frac{\partial f(\phi)}{\partial \phi} \frac{\partial \phi}{\partial t} + \alpha \left( \frac{\partial \phi}{\partial x} \right)\frac{\partial^2 \phi}{\partial x \partial t} \right]\\ &= \int_{\Omega}\left[ \frac{\partial f(\phi)}{\partial \phi} – \alpha \frac{\partial^2 \phi}{\partial x^2} \right]\frac{\partial \phi}{\partial t} +\int_{\partial \Omega} \frac{\partial \phi}{\partial x}n \frac{\partial \phi}{\partial t}\\ &= -\int_{\Omega}L_\phi \left( \frac{\partial \phi}{\partial t} \right)^2 \\ &\leq 0. \end{align*}\]

数值算例

我们以 Lesar [1] 中的一个例子来说明交流方程. 假设阶参数函数 \(u(x)\) 在网格点上的取值如下

u(x_i,t=0), i=1,2,...,15:
    -1 -1 -1 -1 -1 -0.9 -0.5 -0 0.5 0.9  1  1  1  1  1 

考虑自由能表达式\[ \mathfrak{F}=\int_{\Omega} \left\{ f(u) + \frac{\alpha}{2} \left( \frac{\partial u}{\partial x} \right)^2 \right\}, \tag{7a}\]其能量函数定义为\[ f(u)=4 \beta \left(-\frac{1}{2} u^2+ \frac{1}{4}u^4 \right),\]其在 \(u=0\) 处达到最大值, 在 \(u=-1,1\) 处达到它的最小值. 需要注意的是函数 \(f\) 的表达式与任何物理相关, 而是为了近似模拟一个系统的两相能量相等的现象表现而选择的. 下图是展现界面 (左) 和能量 (右) 的示意图.

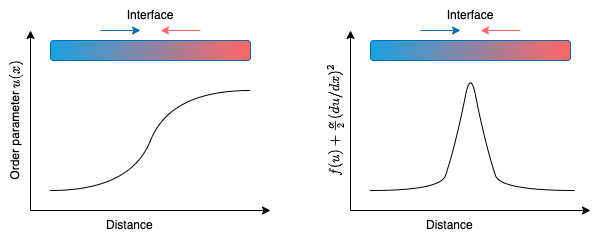
对应的 E-L 方程为\[ u_t = \alpha u_{xx}-4 \beta \left(-u+u^3 \right). \tag{7b}\]其中两个参数的意义为: \(\alpha\) 决定了界面能量大小, \(\beta\) 决定了局部自由能大小. 当比值 \(\alpha/\beta\) 增大, 界面能的大小会变大, 因此系统中的界面应该会变少.

考虑具有周期边界条件的一维问题. 该方程的计算过程如下. 令区域为 \((0,100)\) 并选取空间和时间步长 \(\Delta x=1, \Delta t=0.01\).

1. 选取\(u\) 在网格点上的初值, 这些初值随机分布在区间 \((-0.1, 0.1)\) 内;
2. 由 \(u\) 的值利用 (7a) 计算能量 \(\mathfrak{F}\):\[ \mathfrak{F}_i^n =\Delta x \left( \frac{\alpha}{2} \left( \frac{u_{i+1}^n-u_{i-1}^n}{2\Delta x} \right)^2 + f(u_i^n) \right),\]
3. 利用 (7b) 计算 \(u\) 在下一个时间层的值:\[ u_i^{n+1} = u^n+\Delta t \left( \alpha \frac{u_{i+1}^n-2u_i^n+u_{i-1}^n}{(\Delta x)^2} – 4 \beta(u_i^n+(u_i^n)^3) \right)\]
4. 返回步骤 2 并重复, 直到能量收敛到极小值.

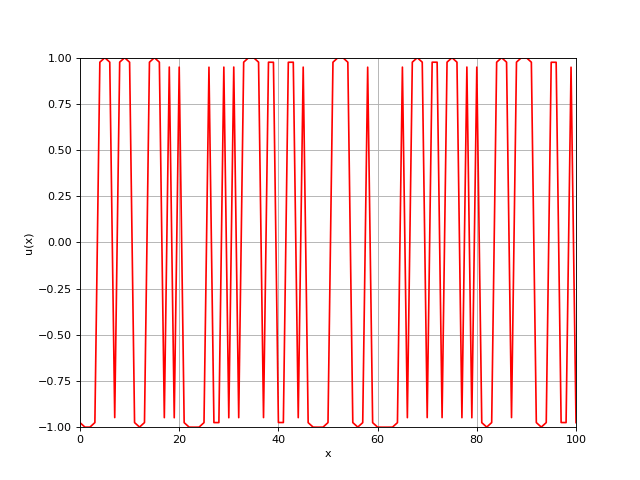
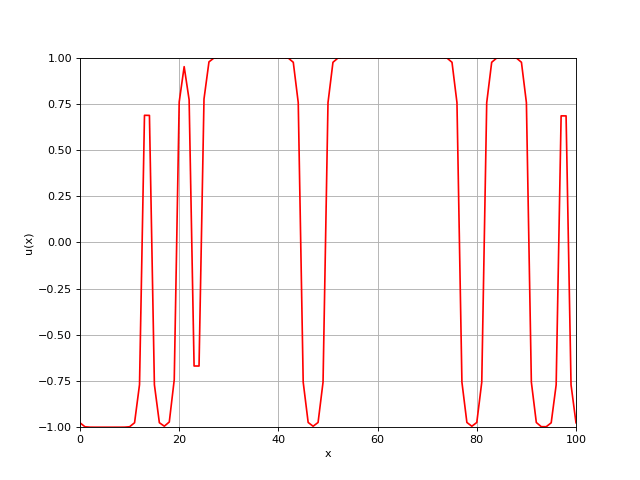
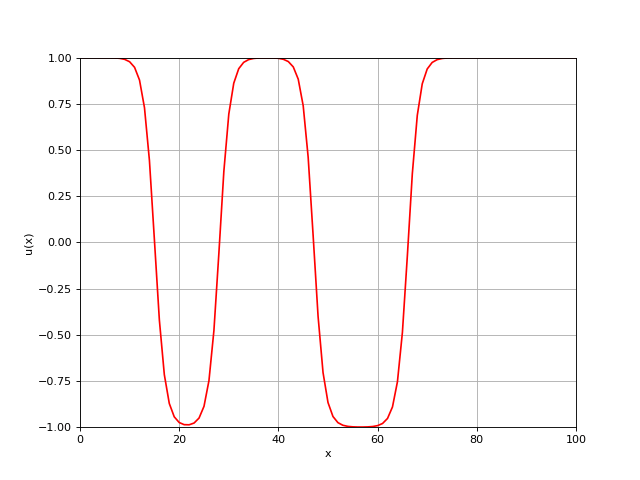
固定 \(\beta=1.0\), 我们测试了三种情况: \(\alpha/\beta=0.1, 1.0, 10\), 稳定状态如下图所示. 我们可以看到, 随着 \(\alpha/\beta\) 增大, 界面的数量在减小.

参考

[1] R. LeSar, Introduction to computational materials science: fundamentals to applications. Cambridge ; New York: Cambridge University Press, 2013.
[2] 变分法简介.