Runge-Kutta-Fehlberg 方法在抛物方程中的应用
热传导方程
为简化表述, 考虑区间 \((0,1)\) 上的一维热传输方程\[ \begin{align*} \frac{\partial u}{\partial t} &=\frac{\partial^2 u}{\partial x^2} , && (\text{方程})\\ u(x,t) &= u_0(x), && (\text{初值})\\ u(0,t) &= u(1,t) = 0. && (\text{边值}) \end{align*} \tag{1}\]上面这个方程是最简单的一种抛物偏微分方程, 它描述了, 比如导热棒上的, 温度随时间的变化过程. 具体地, \(u(x,t)\) 代表点 \(x\) 处在时间 \(t\) 时的温度. 边界条件说明导热棒上端点处的温度始终为零. \(u_0\) 表示初始状态下的温度分布.
上述抛物方程的适定性可以利用现代偏微分方程的理论来说明, 即先证明存在唯一的弱解再利用正则性理论来明该弱解就是满足上述方程的强解 (即所谓的解析解). 我们简述这个过程如下. 利用一个光滑的测试函数 \(v \in C_0^\infty(0,1)\) 乘以方程两边并积分, 再利用分步积分公式可得如下变分形式\[ \int_{0}^1\frac{\partial u}{\partial t}v dx = \int_{0}^1 \frac{\partial ^2u}{\partial x^2} v dx = – \int_{0}^1 \frac{\partial u}{\partial x} \frac{\partial v}{\partial x} dx.\]
定义 1. (弱解 [2]) 如果函数 \(u\in L^2(0,1; H^1_0(0,1))\) 满足 \(\frac{du}{dt} \in L^2(0,1; H^{-1}(0,1))\) 并且
1. \( \langle \frac{\partial u}{\partial t},v \rangle_{H^1_0(0,1)} + \int_{0}^1 \frac{\partial u}{\partial x} \frac{\partial v}{\partial x} dx = 0\), \(\forall v\in H^1_0(0,1)\);
2. u(x,0) = u_0(x);
那么我们称 \(u\) 为抛物方程 (1) 的弱解.
弱解的存在惟一性证明虽然有成熟的理论基础, 但是也相当繁琐, 其中需要利用一些经典的泛函分析内容, 有兴趣的读者最好具备泛函的基础并参考 Evans 的偏微分方程教材 [2] 中关于抛物方程的部分. 在理论上理解抛物方程存在唯一解之后, 我们就可以考虑它的数值离散了: 首先利用有限差分进行空间离散, 将原来的连续问题简化为一个近似的初值问题; 然后考虑利用本文的主角 —- Runge-Kutta-Fehlberg (RKF) —- 进行求解.
初值问题
有限差分是最古老的数值方法之一, 具有数值格式简单, 易于编程实现等优点. 所以对于空间离散 \((x_0:=0, x_1, \ldots, x_N:=1)\), 我们将二阶导数的差分格式 (二维空间类似)\[ \frac{\partial^2 u}{\partial x^2}(x_i,t) \approx \frac{u_{i+1}-2u_{i}+u_{i-1}}{h^2}, \tag{2}\]代入原方程, 我们就得到一个新的初值问题: 求解向量 \([u_0, \ldots, u_N](t)\in \mathbb{R}^{N+1}\):\[ \frac{d u_i}{dt} = \frac{u_{i+1}-2u_{i}+u_{i-1}}{h^2} , \quad i=1,2,\ldots, N-1, \tag{3}\]其中, 由于边值是已知的 \(u_0=u_N=0\), 所以未知量的个数为 \(N-1\). 基于此考虑, 问题 (3) 可以简化为: 求向量 \(\textbf{u}(t):=[u_1, \ldots, u_{N-1}](t)\in \mathbb{R}^{N-1}\) 满足\[ \frac{d\textbf{u}}{dt} =f(\textbf{u}):=\begin{bmatrix} \vdots\\ \frac{u_{i+1}-2u_{i}+u_{i-1}}{h^2} \\ \vdots \end{bmatrix}, \quad \textbf{u}(0) = \begin{bmatrix} u_0(x_1)\\ \vdots\\ u_0(x_{N-1}) \end{bmatrix},\ u_0=u_N=0. \tag{4}\]问题 (4) 就是一个非常典型的常微分方程初值问题. 下面就可以直接利用 RKF 进行求解了. 从这里可以看出每计算一次函数 \(f(\textbf{u})\) 的复杂度为 \(O(N)\), 并不是我们在数值分析教材中看到的标量函数, 所以如果空间离散的规模增大, 对应的函数计算也会增大. 另外, 许多实际问题并不是一维的, 更多是二维或三维的物理空间, 所以计算量的增加速度将是 \(O(N^2)\) 或者 \(O(N^3)\)! 这样的计算量几乎是病态增加的, 所以高阶的 Runge-Kutta (RK) 方法并不一定是一个好的选择; 相反地, 低阶方法在实际应用中是最普遍的, 如 RK4, RKF45 等.
关于时间离散的讨论
我们知道前向 Euler 方法是最简单的求解初值问题 (4) 的显式格式, 定义如下:\[ \frac{u_{i}^{j+1}-u_{i}^j}{k} = \frac{u_{i+1}^j-2u_{i}^j+u_{i-1}^j}{h^2}, \tag{5a}\]或者\[ \frac{\textbf{u}^{j+1}-\textbf{u}^j}{k} = f(\textbf{u}^j). \tag{5b}\]其中, \(k,h\) 分别是时间和空间步长. 这种显式方法又称为四点格式, 下图给出了格式中的依赖关系.
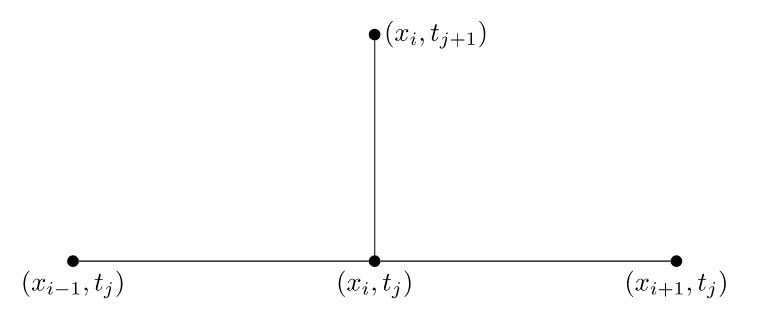
实际应用中, 我们可能需要依照如下步骤来实现 Euler 方法:
- 计算初始条件 \(u_{i}^0=u_0(x_i), \ i=1,\ldots,N-1\).
- 边值条件表明第 \(j+1, j=0,1,\ldots,N_t-1\), 层的边值 \(u^{j+1}_0=u^{j+1}_{N}=0\), 内部点处的值满足\[ u_{i}^{j+1} = u_{i}^j+\frac{k}{h^2}\left( u_{i-1}^j-2 u_i^j+u_{i+1}^j \right), \quad i=1,\ldots,N-1.\]
可以证明, 为保证 Euler 方法 (5a,5b) 的稳定性, 时间步长和空间步长必须满足如下条件 [3]:\[ \frac{k}{h^2}\leq \frac{1}{2}.\tag{6}\]稳定性条件 (6) 告诉我们, 如果想要利用 Euler 方法 (5) 得到一个令人满意的数值解, 通常需要足够小的空间步长 \(h\); 这也意味着时间步长 \(k\) 也必须足够小, 关于时间的迭代就会更加耗时. 一个可行的方法就是采用比 Euler 法更高阶的 Runge-Kutta 方法.
Fehlberg [1] 在其论文中指出热方程的 RK4 方法相比于 Euler 方法 (A.1) 的优点并不明显. 原因如下: 1. RK4 方法的稳定性条件是 \(k/h^2< 0.7\), 优越性并不明显; 2. RK4 每一次时间迭代需要更多的计算量. 因此反观 Euler 方法, 如果我们要求的精度不太高, 其优点是明显的.
由于显式方法存在稳定性条件的限制和实际应用中因为方程或者数学模型的多样性和复杂性, 再加上需要考虑计算量等因素, 时间步长需要不断调整到合适的大小, 通常这不是一个简单直观的问题. 但是另一方面, 如果我们利用隐式方法, 如 Crank-Nicolson, 因为是无条件稳定的, 所以可以避免稳定性条件 (6). 但是, 每一次迭代都需要求解一个同规模的线性系统, 相对显式方法增加了巨大的计算量.
RKF 提供了一个不错的解决办法. 由于 RKF 方法并不是单纯的显式 RK 方法, 它具有根据已计算的数值解自动调节时间步长的能力. Fehlberg 做了这样一个实验: 在 8 位精度的计算机上采用尽可能高的局部截断误差要求, 利用低价 RKF 方法求解热方程. 数值结果表明, 在相当多次时间迭代后, 数值解的有效数字依旧可以保持在 5-6 位, 而且不会出现稳定性问题. 我们在后面的数值实验中, 以现有计算条件来验证 RKF 方法在求解热方程中的有效性. 关于 RKF 方法读者可以参考另一篇文章: 常微分方程初值问题: Runge-Kutta-Fehlberg 方法.
数值结果
例 1. 考虑 Fehlberg 在 [1] 中给出了一个热传输方程例子:\[ \frac{\partial u}{\partial t} =\frac{e^{2-u}}{4(2+x^2)}\frac{\partial^2 u}{\partial x^2} , \quad x\in (0,1), \tag{7}\]其中, 边值和初值都由如下的解析解给出\[ u(x,t) = 2+\log(1+t)-2 \log(2-x^2).\]在数值计算中: 1. 将物理空间 (0,1) 等分成 16 段, 即步长 \(h=1/16\); 2. 将 RKF45 的数值精度设置为 \(10^{-2}\) 到 \(10^{-8}\); 3. 时间 \(t=100\).
因为具有不同的二阶导数系数, 所以本例中的方程的离散格式与 (3) 稍有不同:\[ \frac{d u_i}{dt} = \frac{e^{2-u_i}}{4(2+x_i^2)}\frac{u_{i+1}-2u_{i}+u_{i-1}}{h^2}. \tag{8}\]另外, 实际计算中需要考虑到方程 (7) 的边值并不总是零. 下面的表格中我们列出了对应的数值结果, 从中可以看出误差趋于稳定, 这个结果与 Fehlberg [1] 中的计算结果非常接近, 也说明了 RKF 方法在热传输问题中的有效性. 随着精度要求不断提高, 最终的误差并没有对应的减小, 这主要是因为空间离散是固定的并限制了误差的上限, 最后导致时间离散产生的误差远小于空间离散产生的误差, 所以总的误差趋于稳定. 应对的办法自然是缩小空间步长, 当然这样除了增加问题的规模之外不会引起其它的计算困难, 数值离散过程是完全相同的.
RKF45(TOL) step max error
1e-2 795 1.1044e-03
1e-4 802 1.1088e-03
1e-6 1390 1.1088e-03
1e-8 3841 1.1088e-03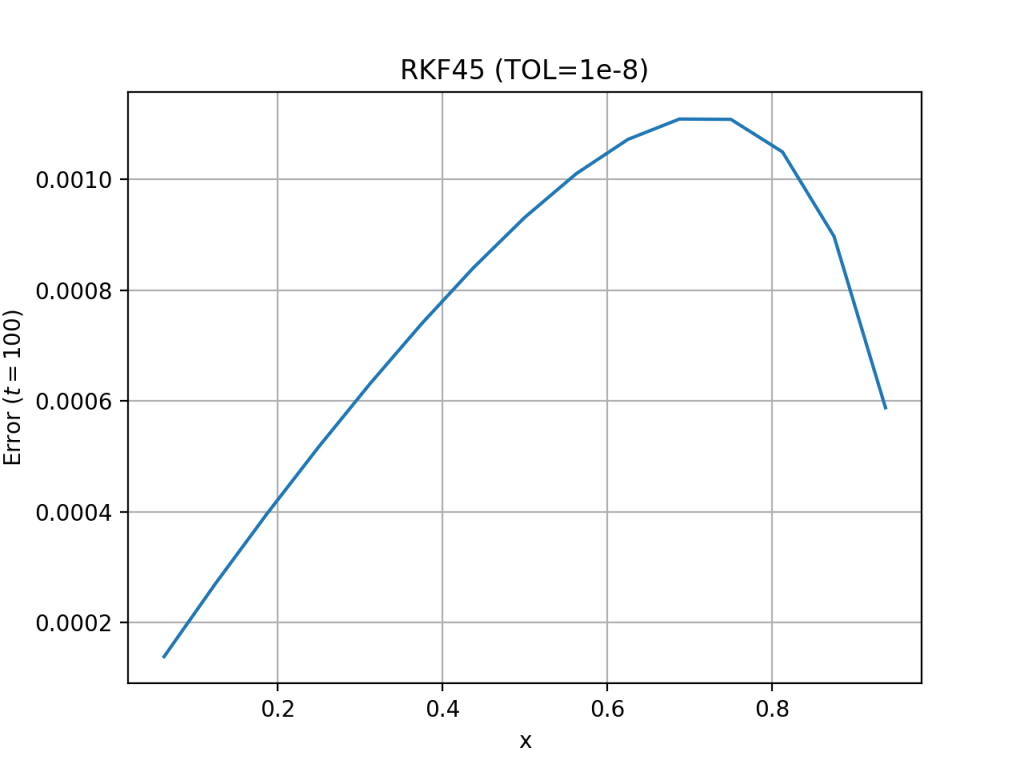
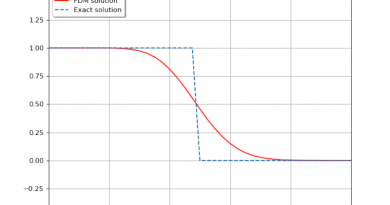
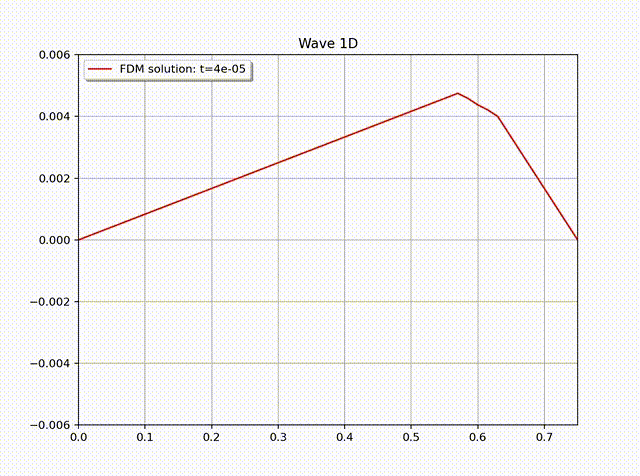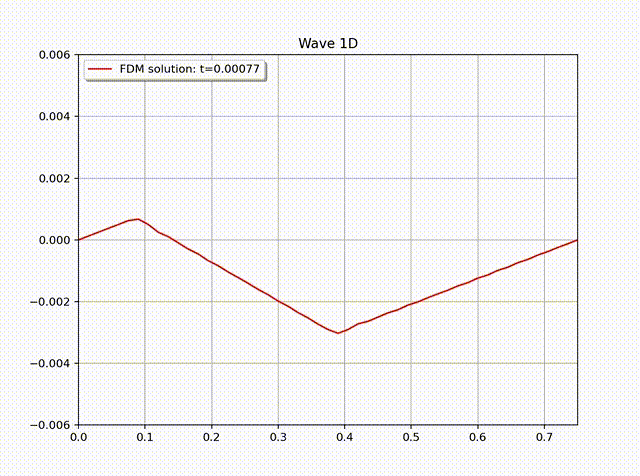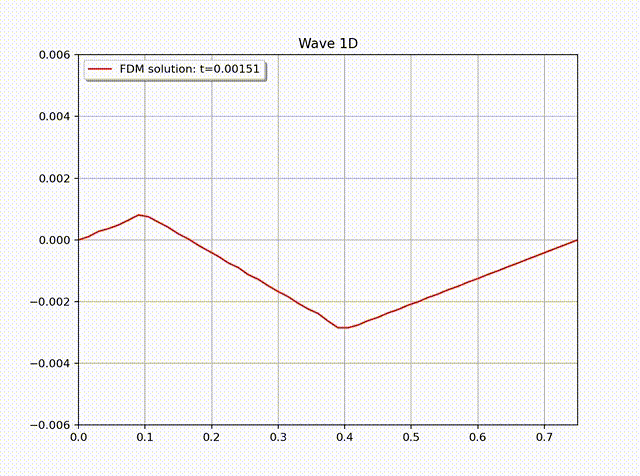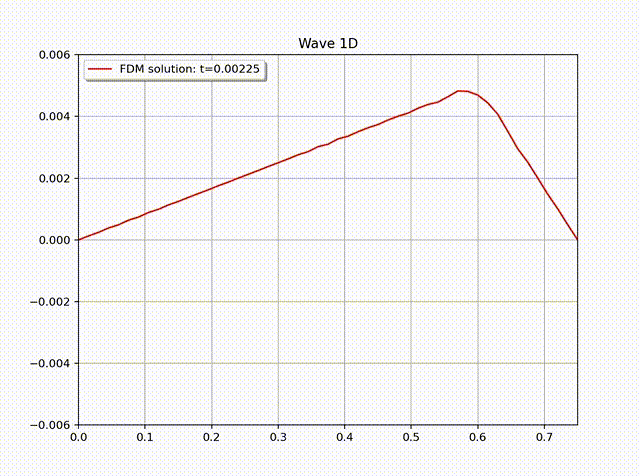
例 2. 我们考虑一个自然冷却过程:\[ \begin{align*} \frac{\partial u}{\partial t} &=\frac{\partial^2 u}{\partial x^2} , \\ u(0,t) &= u(1,t) = 0. \end{align*}\]同样地, 将物理空间步长 \(h=1/16\), 并设置初值为 \(\textbf{u}(x_i)=1, i=1,\ldots, 15\); 因为这是一个自然冷却过程, 由于边界条件始终是零, 物理常识告诉我们温度分布最终也会全部变成零. 我们用 RKF45 方法模拟的过程见下面的动图.

参考
[1] Erwin Fehlberg (1969) Low-order classical Runge-Kutta formulas with stepsize control and their application to some heat transfer problems. Vol. 315. National aeronautics and space administration.
[2] Evans, L. C. (2010). Partial differential equations. In Graduate studies in mathematics (2nd ed.). American Mathematical Society.
[3] Jovanović, B. S., & Süli, E. (2014). Analysis of Finite Difference Schemes. In Finite Difference Schemes and Partial Differential Equations.
附录
例 2 的 python 实现.
# Runge-Kutta-Fehlberg 45 (improved) method
# for heat transfer (parabolic) equation.
#
# --- by numanal.com, 2021/21/24
#
import numpy as np
import matplotlib.pyplot as plt
class my_ode_ivp:
def __init__(self, fun, t_span, y0, yfun=None):
self.fun = fun
self.yfun = yfun
self.t_span = t_span
self.y0 = y0
self.tall = None
self.yall = None
def rkf45(self, TOL=1e-6, hmin=1e-7, hmax=0.2, improved_flag=False):
# improved_flag indicate to use improved rkf45 or classical rkf45
#
flag = True
h = hmax
yi = self.y0
ti = self.t_span[0]
N, Ny = 1000, 1 # Ny is the total number of computed y
yall = np.zeros((yi.shape[0], N))
tall = np.zeros(N)
yall[:,0] = yi
tall[0] = ti
while flag:
k1=h*self.fun(ti, yi)
k2=h*self.fun(ti+.25*h, yi+.25*k1)
k3=h*self.fun(ti+3*h/8, yi+3*k1/32+9*k2/32)
k4=h*self.fun(ti+12*h/13, yi+1932*k1/2197-7200*k2/2197+7296*k3/2197)
k5=h*self.fun(ti+h, yi+439*k1/216-8*k2+3680*k3/513-845*k4/4104)
k6=h*self.fun(ti+.5*h, yi-8*k1/27+2*k2-3544*k3/2565+1859*k4/4104-11*k5/40)
# compute |y_{i+1}-w_{i+1}|/h
D = k1/360-128*k3/4275-2197*k4/75240+k5/50+2*k6/55
R = np.linalg.norm(D)/h
if R<TOL: # accurate is acceptable
ti += h
yi += 25*k1/216+1408*k3/2565+2197*k4/4104-k5/5 # rkf45
if improved_flag: # imaproved rkf45
yi += D
# save new yi
if Ny>=yall.shape[1]:
yall = np.hstack((yall, np.zeros((yi.shape[0],1000))))
tall = np.concatenate((tall, np.zeros(1000)))
tall[Ny]=ti
yall[:,Ny]=yi
Ny += 1
# compute q
q = .84*(TOL/R)**(.25)
# new size for step i-th or (i+1)-th
if q<=.2:
h=.2*h
elif q>=4:
h=4*h
else:
h *= q
if h>hmax:
h=hmax
if ti >= self.t_span[1]:
flag=False
elif ti+h > self.t_span[1]:
h = self.t_span[1]-ti
if h<hmin:
flag=False
self.tall = tall[:Ny]
self.yall = yall[:,:Ny]
def plot(self):
fig = plt.figure()
ax = plt.gca()
ax.set_facecolor('white')
plt.ion()
h, N = 1/16, 15
x = np.linspace(h, 1, N, endpoint=False)
nf = self.yall.shape[1]//20
for i in range(0, self.yall.shape[1], nf):
plt.cla()
plt.plot(x, self.yall[:,i], '-', label='RKF45 solution')
plt.xlabel('x')
plt.ylabel('u')
plt.title('RKF45 (TOL=1e-6)')
plt.ylim(-.1, 1.1)
plt.grid(True)
plt.pause(.1)
plt.ioff()
plt.show()
# setting for ode: f(t,y), y0, t_span
def f(t, y):
h, N = 1/16, 15
x = np.linspace(h, 1, N, endpoint=False)
yleft = 0.
yright = 0.
ans = np.zeros(N) # size of y is N
ans[0] = (y[1]-2*y[0]+yleft)/(h**2)
for i in range(1,N-1):
ans[i] = (y[i+1]-2*y[i]+y[i-1])/(h**2)
ans[-1] = (yright-2*y[-1]+y[-2])/(h**2)
return(ans)
# exact solution
def yfun(t,x):
return (2+np.log(1+t)-2*np.log(2-x**2))
if __name__=='__main__':
h, N = 1/16, 15
x = np.linspace(h, 1, N, endpoint=False)
y0 = np.ones(N)
# y0[6] = 10.
t_span = np.array([0., 1])
# solve and print sol
ode = my_ode_ivp(fun=f, t_span=t_span, y0=y0)
tol = 1.0e-6
ode.rkf45(TOL=tol, hmin=.0001, hmax=.25, improved_flag=False)
# yend = ode.yall[:,-1]
# print("{:16d} {:.4e}".format(ode.tall.shape[0], np.max(np.abs(ode.yall[:,-1]-ode.yfun(ode.t_span[1], x)))))
ode.plot()