数值分析
帕德逼近 (Padé approximation)
引言 Padé 逼近多项式 \(R_{n
数学基础
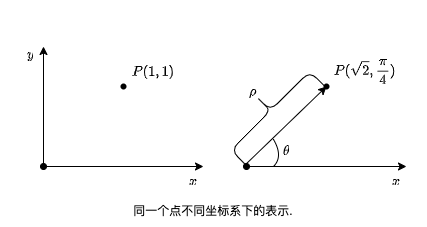
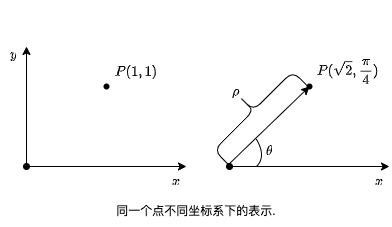
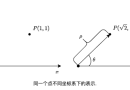
From Cartesian to polar (从笛卡尔坐标到极坐标)
本文档提供了从笛卡尔坐标转换为极坐标的简单介绍。转换过程包括使用勾股定理计算到原点的距离，以及使用反正切函数并进行适当的象限调整来确定角度。主要内容包括基本转换公式、处理坐标轴上的特殊情况，以及在编程语言中使用atan2函数的实际实现。示例演示了不同象限中点的转换过程。
数值方法
A note on Gudi’s analysis of the IPDG method
In this note, we give an alternative proof for an estimate in Gudi’s method, where the author uses a result in a posteriori result without proof.
科普读物
为什么艾伦·图灵 (Alan Turing) 说科学是一个微分方程而宗教是一个边界条件?
图灵说过一句话: science is a differential equation and religion is a boundary condition. 翻译过来就是: 科学是一个微分方程而宗教是一个边界条件. 这里的宗教我们大概可以替理解成国人的信仰. 对这句话理解一些人有一些非常独到的理解, 也许会对从事科学研究的人有某些启发.
