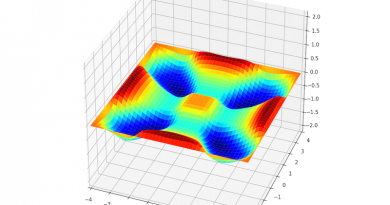
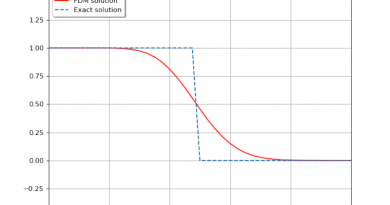
一维波方程的有限差分方法
本文中, 我们详细描述了求解一维波方程的一种显式有限差分方法, 并且给出了一些数值实验.
一维波方程
我们考虑如下定义在弦 \(I=[0,L]\) 上的波方程:\[\begin{align} \partial_t^2 u &= c^2\partial_x^2 u +f && \text{in } I\times (0,T), \tag{1}\\ u(x,0) &= u_0 && \text{in } I, \\ \partial_t u(x,0)&=u_1 && x\in I, \\ u(0,t) &=0 && t\in (0,T], \\ u(L,t) &=0 && t\in (0,T], \\\end{align}\] 其中, \(L\) 是弦的长度, \(c\) 是波速, \(u_0\) 和 \(u_1\) 是波的初值和初始速度.
有限差分方法
为了离散波方程, 我们需要定义一族弦上的一致剖分 \[ 0=x_0 < x_1 < \ldots < x_{n-1}< x_n=L, \] 并且对时间区间进行剖分 \[ 0=t_0 < t_1 < \ldots < t_{m-1}< t_m=T, \] 其中, 我们令 \(h, \tau\) 分别表示物理空间和时间空间步长大小.
由物理和时间剖分, 我们令 \(u_i^k\) 表示精确解在网格点 \((x_i,t_k)\), \(i=0,\ldots,n\), \(k=0,\ldots ,m\) 上的近似值. 下面, 我们会导出近似触媒所满足的代数方程. 基本的思想就是利用差商来代替导数. 例如, 我们可以用二阶差商来近似二阶导数 \(\partial_t^2 u\):\[ \partial_t^2u(x_i,t_k) \approx D_t^+D_t^-u_{i}^k := \frac{u_i^{k+1}-2u_i^k+u_i^{k-1}}{\tau^2}.\] 类似地, 关于物理空间的二阶导数 \(\partial_x^2u\) 可以近似如下\[ \partial_x^2u(x_i,t_k) \approx D_x^+D_x^-u_{i}^k := \frac{u_{i+1}^k-2u_i^k+u_{i-1}^k}{h^2}.\] 从而, 我们得到如下的对应于连续方程的差分方程\[ \frac{u_i^{k+1}-2u_i^k+u_i^{k-1}}{\tau^2} = c^2 \frac{u_{i+1}^k-2u_i^k+u_{i-1}^k}{h^2} + f(x_i,t_k),\] 利用上面的等式, 可以得到基本的有限差分格式\[ u_i^{k+1} =2u_i^k-u_i^{k-1} + \left( c\frac{\tau}{h} \right)^2 (u_{i+1}^k-2u_i^k+u_{i-1}^k) + \tau^2f(x_i,t_k). \tag{2}\]其中, \(i=1,2,…,n-1\).
初值条件
由初值条件可以直接得到\[ u_i^0 = u_0(x_i). \tag{3}\]
数值格式 (2) 当 \(j=0\) 时是没有定义的, 因为 \(u^{-1}_i\) 是初值条件不能直接给出的. 但是我们可以利用如下两个方法得到 \(u^1_i\):
- 一种方法是使用初始条件和前向 Euler 方法来得到 \(u^1_i\) \[ u^1_i = u^0_i + u_1(x_i) \tau \tag{4}\] 然后利用数值格式 (2) 来得到其它数值解 \(u^k_i,k=2,3,…,m\).
- 通过利用一阶导数的中心差分数值格式 \[ \partial_tu(x_i,t_0)\approx \frac{u^{1}_i-u^{-1}_i}{2\tau}, \] 我们有 \(u_i^{-1} = u^{1}_i – 2 \tau \partial_tu(x_i,t_0)\), 从而代入到 (2) (\(k=0\)) 得到 \(u_i^1\) 所满足的方程 \[ u_i^{1} =2u_i^{0}-(u^{1}_i – 2\tau \partial_tu(x_i,t_0)) + \left( c\frac{\tau}{h} \right)^2 (u_{i+1}^{0}-2u_i^{0}+u_{i-1}^{0}) + \tau^2f(x_i,t_k), \] 即, \[ u_i^{1} =u_i^{0}+\tau \partial_tu(x_i,t_0) + \frac{1}{2}\left( c\frac{\tau}{h} \right)^2 (u_{i+1}^{0}-2u_i^{0}+u_{i-1}^{0}) + \frac{1}{2}\tau^2f(x_i,t_k). \tag{5} \]
边界条件
由 \(u(0,t)=u(L,t)=0\) 可知 \[ u_0^k = u_{n}^k =0.\]
有限差分算法
综上, 我们得到如下显式有限差分算法
- 利用 (3) 计算 \(u_i^0\);
- 通过 (4) 或 (5) 计算 \(u_i^1\), \(i=1,…,n-1\), 并且赋予边界条件 \(u_{0}^1=u_{n}^1=0\);
- 对每一个时间层 \(j=1,…,m-1\), 通过 (2) 计算 \(u_i^{k+1}\), \(i=1,…,n-1\) 并且赋予边界条件 \(u_{0}^{k+1}=u_{n}^{k+1}=0\).
注意, 这里的显式是指当前时间层上的未知量仅仅依赖于已知时间层上的数值解, 不依赖于当前所求的未知量. 我们可以回想求解常微分方程的显式欧拉算法来帮助理解.
数值算例
为了验证有限差分法的收敛速度, 我们需要对比解析解与数值解之间的误差, 即, 计算 \[ \text{误差} = \|e^k\|_{\ell^2}:=\left( \tau h\sum_{i=1}^{N_x}\sum_{j=1}^{N_t} |u_i^k-u(x_i,t_k)|^2 \right)^{1/2}.\]
例 1. 我们首先考虑方程具有如下解析解的方程 (1), 同时该解也同时满足差分格式 (2): \[ u(x,t) = x(L-x)(1 + t/2), \tag{6}\] 其中, 我们令 \(L=2.5,c=1.5,T=18.\) 容易验证函数 \(u\) 确实精确满足差分格式 (2). 通过数值计算可以精确得到解析解.
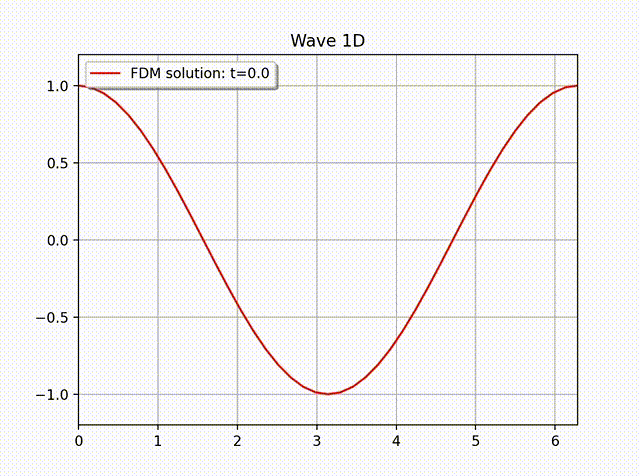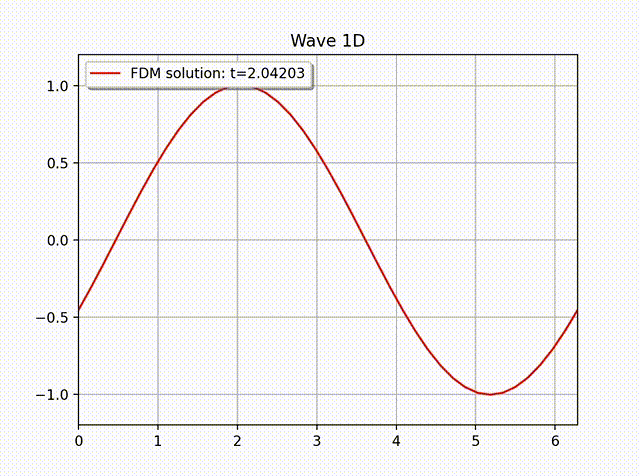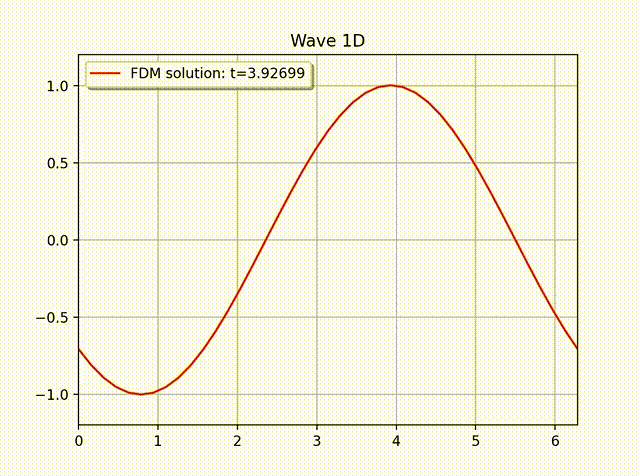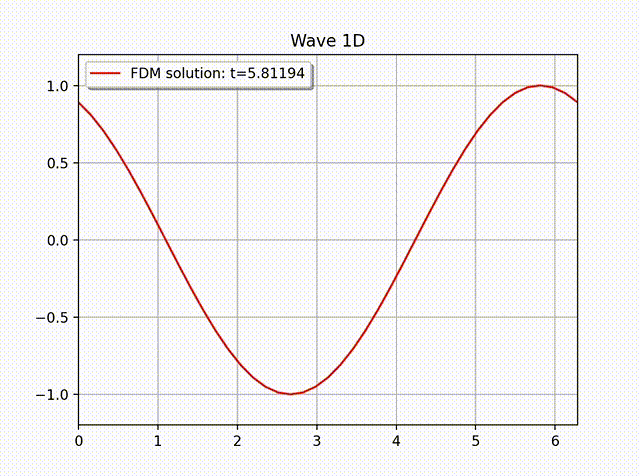
例 2. 假设方程 (1) 具有如下解析解 \[ u(x,t) = A \sin \left( \frac{\pi}{L}x \right) \cos \left( \frac{\pi}{L}ct \right).\]
通过直接计算可知, 右端项 \(f=0\), 且满足边界条件 \(u(0,t)=u(L,t)=0\). 初值条件为 \(u(x,0)=A \sin \left( \frac{\pi}{L}x \right)\) 和 \(u'(x,0)=0\). 在实际计算中, 我们令 \(A=L=1,T=3, c=1\). 下面的图片显示了有限差分解的图像, 其中物理空间和时间空间步长大小为 \(N_x=20, h=L/N_x; \tau=h/c=L/(cN_x)\approx 64\).
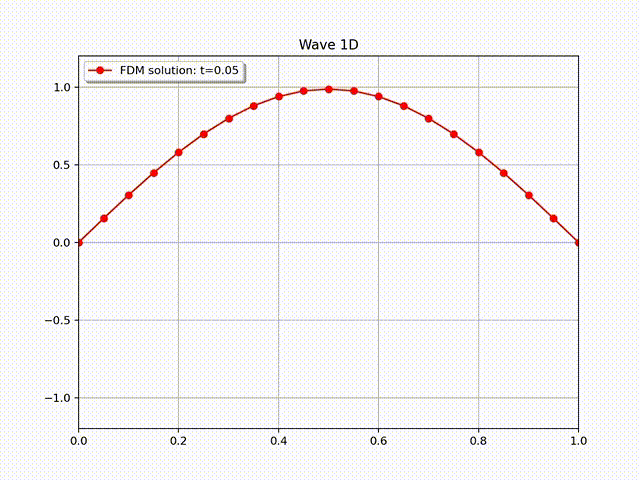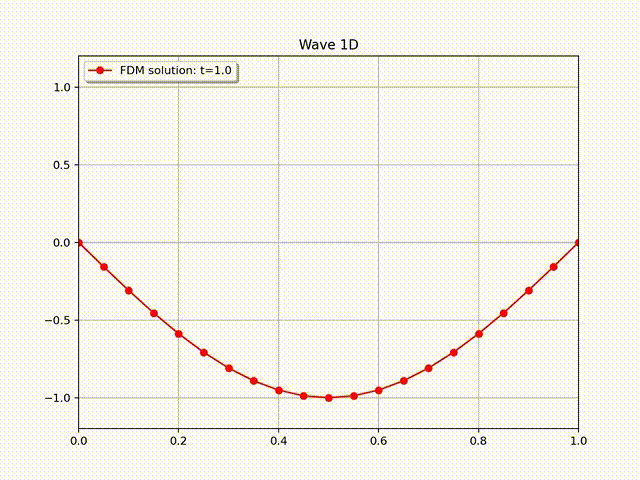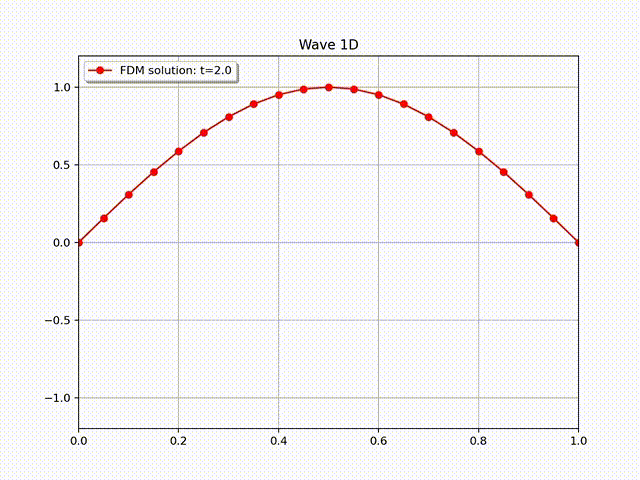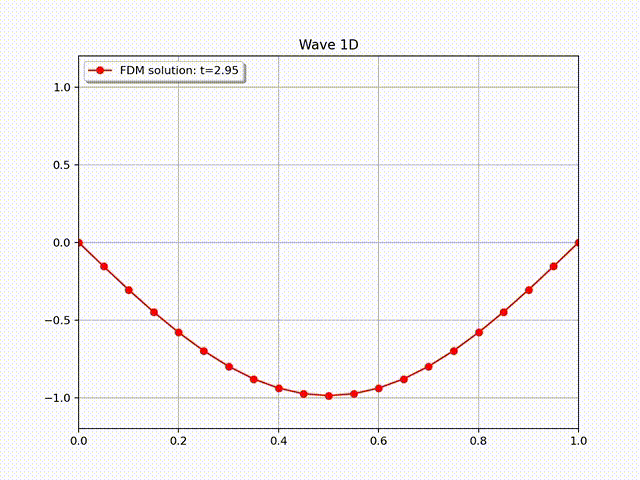
为了更清楚地看到收敛速度的变化, 我们在下面的表格中列出了误差随网格大小的变化数据, 从中可以看出误差关于物理步长大小的收敛速度为 \(O(h^2).\)
| \(N_x/N_t=2000\) | 误差 | 收敛率 |
| 20 | 4.8015e-03 | |
| 40 | 1.1967e-03 | 2.00 |
| 80 | 2.9591e-04 | 2.01 |
| 160 | 7.0734e-05 | 2.06 |
| 320 | 1.4441e-05 | 2.29 |
例 3. 考虑拨动吉它弦的数值模拟, 即满足如下初值的方程 (1) \[ u_0=\begin{cases} ax/x_0 & x<x_0,\\ a(L-x)/(L-x_0) ,& x\geq x_0. \end{cases}\]
其中, \(L=.75\)m 是吉它弦的长度, \(x_0=0.8L, a=0.005\)m, 波动频率 \(\nu=440\) Hz. 另外, 令 \(c=\lambda \nu=2L \nu=660\) m/s. 因为没有其它外力, 所以右端项 \(f=0\); 同时初始速度 \(u_1=0\). 通过计算可知周期 \(T=1/\nu=0.0022727…\)
在数值计算中, 令网格大小为 \(h=L/N_x, \tau=L/(N_xc)\), 其中 \(N_x=50\). 值得注意的是时间步长 \(\tau\) 必须充分小, 尽管这样会增加计算复杂度, 来保证有限差分方法的稳定性. 一般来说, 我们可以通过 CFL 数找到一个 \(\tau\) 的上界, 这个 CFL 数也被用来判断方法是否稳定的准则 (例如参考 [1])\[ CFL = \frac{c_{\max} \tau}{h} \leq C \left( =\frac{\eta}{\pi \sqrt{d}} \right).\] 简单起见, 我们粗略地令 \(\tau\leq h/c\). 在实际应用中, 可以使用这样一个数值作为时间步长的第一个尝试. 下图中展示了有限差分解随时间的变化情况, 其中, \(N_x=50, N_t=102\).
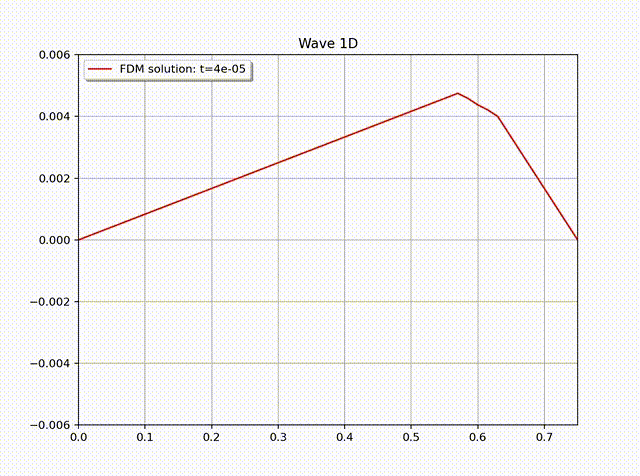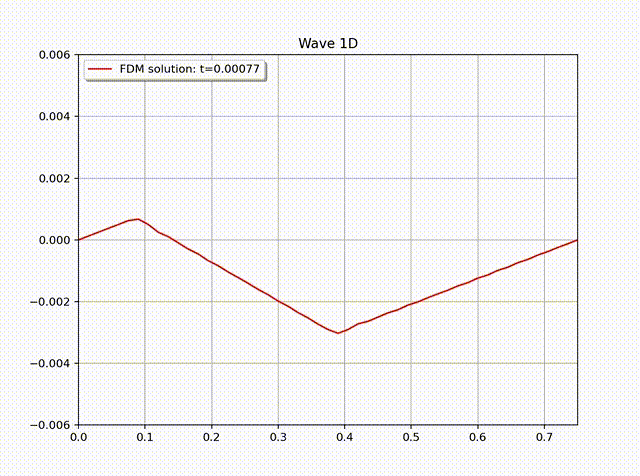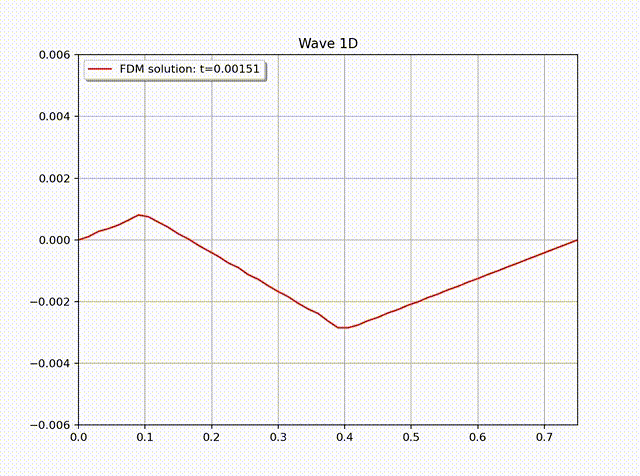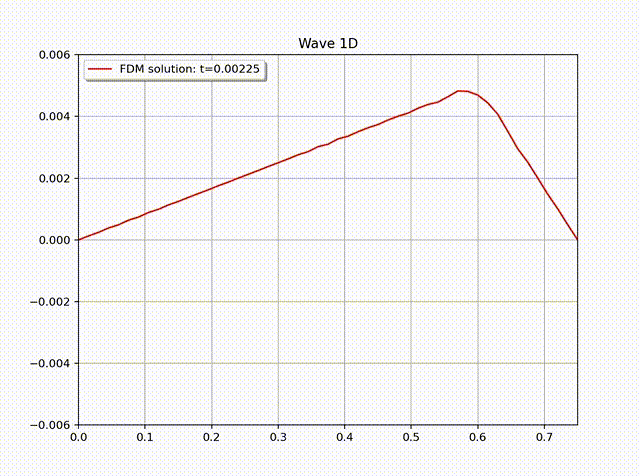
参考
- H. P. Langtangen (2016) Finite difference method for wave motion.
- Jing-Bo Chen, (2011), “A stability formula for Lax-Wendroff methods with fourth-order in time and general-order in space for the scalar wave equation,” GEOPHYSICS 76: T37-T42.
- 常微分方程初值问题: Euler 方法. 数值分析大巴.
附录: Python 源程序
#
# code for FDM-wave1d.md
# -- https://numanal.com 2021/7/26
#
import numpy as np
import matplotlib.pyplot as plt
# # pde example - guitar
# class Wave1d(object):
# def __init__(self):
# self.L = .75
# self.a = 0.005
# self.x0 = .8*self.L
# self.freq = 440
# self.wavelength = 2*self.L
# self.c = self.freq*self.wavelength
# omega = 2.*np.pi*self.freq
# num_periods = 1.
# self.T = 2*np.pi/omega*num_periods
# self.umax = self.a
# def u(self,x,t): # this is not the exact solution here!
# return self.a * np.sin(np.pi*x/self.L) * np.cos(np.pi*self.c*t/self.L)
# def u0(self,x):
# v = np.zeros(x.shape[0])
# for i in range(v.shape[0]):
# if x[i]<self.x0:
# v[i] = self.a*x[i]/self.x0
# else:
# v[i] = self.a*(self.L-x[i])/(self.L-self.x0)
# return v
# def u1(self,x):
# return 0.*x
# def f(self,x,t):
# return 0.*x*t
class Wave1d(object):
def __init__(self):
self.c = 1.
self.L = 1.
self.T = 3.
self.A = 1.
self.umax = self.A
def u(self,x,t):
return self.A * np.sin(np.pi*x/self.L) * np.cos(np.pi*self.c*t/self.L)
def u0(self,x):
return self.u(x,0)
def u1(self,x):
return 0.*x
def f(self,x,t):
return 0.*x*t
def plot(self):
t = np.linspace(0, 2*pde.T, 50)
x = np.linspace(0,pde.L, 20)
plt.figure(figsize=(8, 6), dpi=80)
plt.ion()
for i in range(t.shape[0]):
plt.cla()
plt.title("Wave")
plt.grid(True)
u = pde.u(x,t[i])
plt.plot(x,u, '-r', label="Exact solution: t="+str(int(100*t[i])/100))
# plt.plot(v1*t[i], 0, 'or' , markersize=12)
plt.xlim(x[0], x[-1])
# plt.plot(v2*t[i], 0, 'ob' , markersize=12)
plt.ylim(-1.2, 1.2)
plt.legend(loc="upper left", shadow=True)
plt.pause(.2)
plt.ioff()
plt.show()
# class Wave1d(object):
# def __init__(self):
# self.c = 1.5
# self.L = 2.5
# self.T = 18
# def u(self,x,t):
# return x*(self.L-x)*(1 + 0.5*t)
# def u0(self,x):
# return self.u(x,0)
# def u1(self,x):
# return 0.5*self.u(x, 0)
# def f(self,x,t):
# return 2*(1 + 0.5*t)*self.c**2
# uniform spatial and time space
class Mesh():
def __init__(self,x,t):
self.x = x
self.t = t
# solver class
class Wave1DSolver():
def __init__(self, pde, mesh):
self.pde = pde
self.mesh = mesh
self.Nx = mesh.x.shape[0]-1
self.Nt = mesh.t.shape[0]-1
self.dx = mesh.x[1]-mesh.x[0]
self.dt = mesh.t[1]-mesh.t[0]
self.C2 = (pde.c*self.dt/self.dx)**2
self.u_fdm = None
self.u_exact = pde.u(mesh.x, pde.T)
self.err_l2 = 0.
self.err_l2_final = 0.
def solve(self):
dt, dx, C2 = self.dt, self.dx, self.C2
Nx = self.Nx
uplus = np.zeros(self.Nx+1)
umid = np.zeros(self.Nx+1)
uminus = np.zeros(self.Nx+1)
err_l2 = 0.
# set initial values
x = self.mesh.x
umid = self.pde.u0(x)
du0 = self.pde.u1(x)
# u^1
j=0
for i in range(1,Nx):
# uplus[i] = umid[i]+dt*du0[i]
uplus[i] = umid[i]+dt*du0[i] \
+ .5*C2*(umid[i+1]-2*umid[i]+umid[i-1]) + .5*dt**2 * self.pde.f(self.mesh.x[i],self.mesh.t[j])
uplus[0] = 0; uplus[Nx] = 0 # Enforce boundary conditions
err_l2 += dt*dx * np.sum((uplus-self.pde.u(x,self.mesh.t[j+1]))**2)
uminus[:] = umid
umid[:] = uplus
# gif plot - 1/3
plt.figure(figsize=(8, 6), dpi=80)
plt.ion()
for j in range(1,self.Nt):
for i in range(1,Nx):
uplus[i] = 2*umid[i] - uminus[i] + C2*(umid[i+1]-2*umid[i]+umid[i-1]) + dt**2 * self.pde.f(self.mesh.x[i],self.mesh.t[j])
uplus[0]=0
uplus[Nx]=0
err_l2 += dt*dx * np.sum((uplus-self.pde.u(x,self.mesh.t[j+1]))**2)
self.err_l2_final = np.sqrt( dx * np.sum((uplus-self.pde.u(x,self.mesh.t[j+1]))**2) )
# gif plot - 2/3
if j%np.ceil(t.shape[0]/50) == 1:
plt.cla()
plt.title("Wave 1D")
plt.grid(True)
plt.plot(x,uplus, '-r', label="FDM solution: t="+str(int(1e5*self.mesh.t[j+1])/1e5))
plt.xlim(x[0], x[-1])
plt.ylim(-1.2*self.pde.umax, 1.2*self.pde.umax)
plt.legend(loc="upper left", shadow=True)
plt.pause(.1)
# Switch before next iteration
uminus[:] = umid
umid[:] = uplus
# gif plot - 3/3
plt.ioff()
plt.show()
self.u_fdm = uplus
self.err_l2 = np.sqrt(err_l2)
return 0
def plot(self):
plt.plot(self.mesh.x,self.u_fdm-self.u_exact, '-or', label='Error=FDM-Exact')
# plt.plot(self.mesh.x, self.u_exact, '-db', label='Exact solution')
plt.legend()
plt.show()
if __name__ == "__main__":
pde = Wave1d()
# print(pde.T, pde.c)
# pde.plot()
Nx = 21
x = np.linspace(0, pde.L, num=Nx, endpoint=True)
dt = pde.L/pde.c/Nx; print(dt)
Nt = int(pde.T/dt+1); print(Nt)
# Nt = 801
t = np.linspace(0, pde.T, num=Nt, endpoint=True)
mesh = Mesh(x, t)
solver = Wave1DSolver(pde, mesh)
solver.solve()
print(solver.err_l2, solver.err_l2_final)
# solver.plot()