有限元理论: 尺度论证
有限元理论中, 尺度论证 (scaling argument) 又称为齐次论证 (homogeneity argument), 通常表示将依赖于网格大小的估计简化为不依赖于网格 (或仅依赖于标准单元) 的估计的方法. 它在有限元理论的误差估计中扮演了极其重要的角色.
尺度论证
尺度论证是有限元方法中最常用的技巧之一, 是有限元理论中的一个重要基础知识点.
现在我们以一维空间中的估计为例来说明它的应用. 令 \(0=x_0 < x_1 < \dots < x_n=1 \) 为区间 [0,1] 上的一个剖分, 那么对任意连续函数 \(u\), 我们可以定义它上的分段线性插值为 \(u_I(x_i)=u(x_i),i=0,\ldots,n\). 那么下面的结果是有限元方法中最基本的结论, 它表明了线性插值函数与原函数之间的误差与网格大小之间的关系, 同时这样的结果也说明了, 如果想要得到更加精确的插值函数, 我们必须通过加细网格来缩小网格大小.
引理 1. [2] 令 \(h=\max_{1< i\leq n}(x_i-x_{i-1})\). 那么如下的结论成立 \[ \|u'-u_I'\|_{L^2(0,1)} \leq C h \|u^{\prime\prime}\|_{L^2(0,1)}, \] 其中, 常数 \(C>0\) 与函数 \(u\) 和网格大小 \(h\) 无关. 在证明上述结论的过程中, 我们需要证明在每个小区间上下面的结果成立 \[ \int_{x_{j-1}}^{x_j}e'(x)^2 dx \leq c(x_j-x_{j-1})^2 \int_{x_{j-1}}^{x_j}e^{\prime\prime }(x)^2 dx. \tag{1} \] 这是一个依赖于网格的估计, 通常是不容易证明的, 但是如果通过尺度论证将积分变换标准单元上, 如 \([0,1]\), 结论会更容易证明. 尺度论证其实就是做了一个变量代换: \[ x = x_{j-1} + t (x_j-x_{j-1}), \] 从而由链式法则, \(e(t)=e(x(t)), e'(t)=e'(x)(x_j-x_{j-1}), e^{\prime\prime}(t)=e^{\prime\prime}(x)(x_j-x_{j-1})^2\), 代入 (1) 中可以得到一个与网格无关的估计: \[ \int_{0}^1 e'(t)^2 dt \leq c \int_{0}^1 e^{\prime\prime }(t)^2 dt. \] 上面的过程就是一个典型的尺度论证的例子. 下面, 我们主要考虑三维空间中的结果.
仿射变换
令 \(\hat{K}\) 为参考单元, 其四个顶点分别为 \((0,0,0), (0,0,1), (0,1,0), (1,0,0)\); 令 \(K\) 表示任意一个四面体. 那么, 存在一个唯一的仿射变换 \(F_K:\hat{K} \to K\) 使得对任一点 \(\hat{\mathbf{x}}\in \hat{K}\) 都存在唯一的一点 \[ \mathbf{x} = F_K \hat{\mathbf{x}} = B_K \hat{\mathbf{x}}+b_K \in K, \tag{2} \] 其中 \(B_K\in \mathbb{R}^{3\times 3}\) 为非奇异矩阵并且单元 \(K\) 的体积满足 \(|K|=\frac{1}{6}|\det(B_K)|\). 事实上, 我们有如下等式成立 \[ |K|=\int_{K}d \mathbf{x} = \int_{\hat{K}} |\det(B_K)| d \hat{\mathbf{x}} = |\hat{K}||\det(B_K)|= \frac{1}{6}|\det(B_K)| , \] 其中的参数 \(1/6\) 就是参考单元的体积. 令 \(h_K, \rho_K \) 分别表示单元 \(K\) 的最小的外接圆直径和最大的内接圆直径.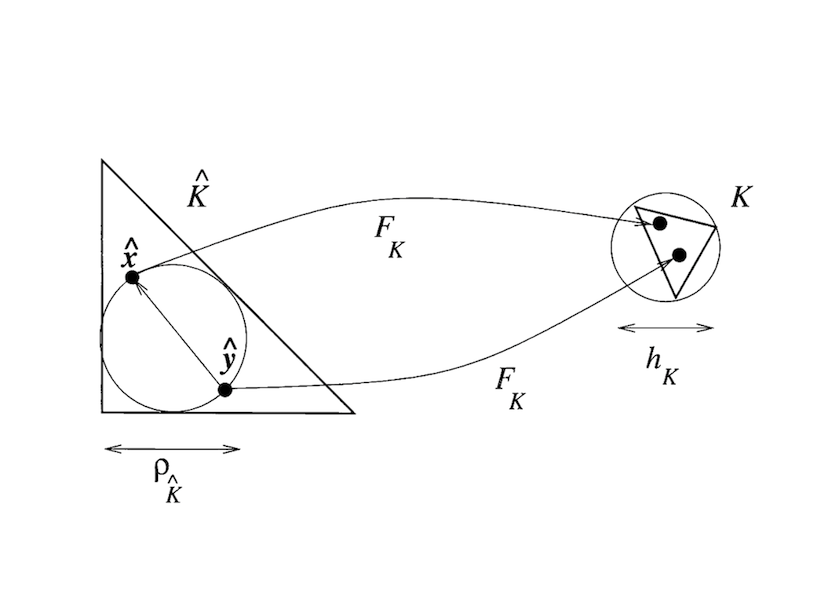
引理2 假设 \(F_K(\hat{K})=K\), 其中 \(F_K\) 是 (2) 中定义的变换. 那么有如下估计成立 \[ \|B_K\|\leq \frac{h_K}{\rho_{\hat{K}}}\quad \text{且}\quad \|B_K^{-1}\|\leq \frac{h_{\hat{K}}}{\rho_K}. \tag{3} \] 同时, 存在两个与 \(\rho_K, h_K\) 无关的常数 \(C_1, C_2\) 满足如下估计 \[ C_1 \rho_K^3\leq |\det(B_K)| \leq C_2 h_K^3. \tag{4} \]
注意, \(h_{\hat{K}}, \rho_{\hat{K}} \) 分别表示参考单元 \(\hat{K}\) 的最小的外接圆直径和最大的内接圆直径, 因此可以看作是常数.
证明. 由矩阵范数的定义可知 \[ \|B_K\|=\sup_{\xi\in \mathbb{R}^3 , |\xi|=1 } |B_K \xi| =\frac{1}{\rho_{\hat{K}}}\sup_{\xi\in \mathbb{R}^3 , |\xi|=1 } |B_K (\rho_{\hat{K}}\xi)| =\frac{1}{\rho_{\hat{K}}}\sup_{\xi\in \mathbb{R}^3 , |\xi|=\rho_{\hat{K}} } |B_K \xi|. \] 如下的证明巧妙地利用了几何方法. 我们知道以 \(\rho_{\hat{K}}\) 为直径的圆包含在参考单元 \(\hat{K}\) 内, 因此, 对任意向量 \(\xi, |\xi|=\rho_{\hat{K}}\), 都存在 \(\hat{K}\) 内的两点 \(\hat{\mathbf{x}}, \hat{\mathbf{y}}\) 使得 \[ \xi = \hat{\mathbf{x}}-\hat{\mathbf{y}}. \] 从而利用变换 \(F_K\) 的定义可知 \[ B_K \xi=B_K(\hat{\mathbf{x}}-\hat{\mathbf{y}})=F_K \hat{\mathbf{x}}-F_K \hat{\mathbf{y}} \] 从而, \(|B_K \xi|\leq |F_K \hat{\mathbf{x}}-F_K \hat{\mathbf{y}}|\leq h_K\). \(\heartsuit\)
Sobolev 空间的同构关系
利用线性变换 \(F_K\), 对于任意一个定义在参考单元上的函数 \(\hat{v}\), 都存在一个定义在单元 \(K\) 上的函数与之对应: \(\hat{v}\to v=\hat{v}\circ F_K^{-1}\). 下面的引理说明了定义在两个单元上的 Sobolev 空间是同构的, 这个结论在有限元方法 (包括间断有限元, 弱有限元, 虚拟元) 的收敛性理论中扮演了重要角色.
引理 3. ([Lemma 5.9, 1]) 设 \(m\geq 0, 1\leq p<\infty\) 且 \(F_K\) 是 (1) 中定义的变换. 那么 \(\hat{v}\to v=\hat{v}\circ F_K^{-1}\) 定义了一个从 \(W^{m,p}(\hat{K})\) 到 \(W^{m,p}(K)\) 上的同构映射并且如下的关系成立 \[ \begin{align*} \left| v \right|_{W^{m,p}(K)} &\leq C \|B_K^{-1}\|^{m} |\det (B_K)|^{1/p} \left| \hat{v} \right|_{W^{m,p}(\hat{K})}, \\ \left| \hat{v} \right|_{W^{m,p}(\hat{K})} &\leq C \|B_K\|^{m} |\det (B_K)|^{-1/p} \left| v \right|_{W^{m,p}(K)}. \tag{5} \end{align*} \]
证明. 我们只证明当 \(m=1\) 时的情况. 利用链式法则容易得到\[ v(x) = v(F_K(\hat{x})),\quad \nabla v(\hat{x}) = B_K^{T}(\nabla v(x)).\]
从而\[ \int_{K}|\nabla v|^p dx = \int_{\hat{K}}|B_K^{-T}\nabla \hat{v}|^p |\det (B_K)| d\hat{x},\\ \int_{\hat{K}}|\nabla \hat{v}|^p d\hat{x} = \int_{K}|B_K^T\nabla v|^p \frac{1}{|\det (B_K)|} dx.\]
因此, 如下两个估计成立\[ \int_{K}|\nabla v|^p dx = \|B_K^{-T}\| |\det (B_K)|\int_{\hat{K}}|\nabla \hat{v}|^p d\hat{x},\\ \int_{\hat{K}}|\nabla \hat{v}|^p dx = \frac{\|B_K\|}{|\det (B_K)|} \int_{K}|\nabla v|^p d\hat{x}.\]
\(\heartsuit\)
注意: 估计 (5) 是一个依赖于单元 (大小和形状) 的结果, 因为利用 (3)(4) 的结果可以得到 \[ \begin{align*} \left| v \right|_{W^{m,p}(K)} &\leq C \rho_K^{-m} h_K^{3/p} \left| \hat{v} \right|_{W^{m,p}(\hat{K})}, \\ \left| \hat{v} \right|_{W^{m,p}(\hat{K})} &\leq C h_K^{m} \rho_K^{-3/p} \left| v \right|_{W^{m,p}(K)}. \end{align*} \] 显然, 对某一网格中所有四面体 \(K\) 来说, 都有 \(\rho_K< h_K\); 如果我们假定 \(h_K\leq C\rho_K\), 即相比于四面体的外接圆直径, 它的内接圆直径不会过分小 (正则或拟一致网格的由来), 那么上面两个估计就只与四面体的大小 \(h_K\) 有关, 与形状无关: \[ \begin{align*} \left| v \right|_{W^{m,p}(K)} &\leq C h_K^{-m+3/p} \left| \hat{v} \right|_{W^{m,p}(\hat{K})}, \\ \left| \hat{v} \right|_{W^{m,p}(\hat{K})} &\leq C h_K^{m-3/p} \left| v \right|_{W^{m,p}(K)}. \end{align*} \] 与一维问题相同, 这样的只依赖于单元大小的结果方便了有限元的误差估计, 也为减少误差提供了直接的线索 (不断加细正则网格得到新的正则网格). 通常, 给定计算区域之后, 网格生成软件都会尽量生成大小不会超过设置的网格大小 \(h\) 的正则网格, 即不会出现过分“扁”的单元, 但是在实际应用中最好首先检查网格是否是正则的.
拓展
尺度论证还有另外的形式. 比如, 在下面的题目的证明中使用的技巧通常也被称为尺度论证.
问题 1 ([1.x.31, 2]) Let \(\Omega\) denote the upper half-plane. Show that no inequality of the form \(\|v\|_{L^2(\partial \Omega)}\leq C\cdot \|v\|_{L^2(\Omega)}^\lambda \cdot \|v\|_{W_2^1(\Omega)}^\mu\) hold, unless \(\lambda\leq 1/2\) and \(\lambda+\mu=1\). (Hint: suppose it holds and consider the functions \(u(x)=Uv(Lx)\) for U and L arbitrary to reach a contradiction.)
证明. Let \(u(x)=Uv(Lx)\), it holds \[ |u|_{W^{k,p}(\Omega)}=UL^{k-n/p}|v|_{W^{k,p}(\Omega)}. \] Here, \(n=2\). If the equation holds, there are \[ U^{-1}L^{1/2}\|u\|_{L^{2}(\partial\Omega)}\leq C \left( U^{-1}L \|u\|_{L^{2}(\Omega)} \right)^{\lambda} \left[\left( U^{-1}L\|u\|_{L^{2}(\Omega)} \right)^{2} +\left( U^{-1}|u|_{W^{1,2}(\Omega)} \right)^{2} \right]^{\mu/2}, \] which reduces to \[ \begin{align*} \|u\|_{L^{2}(\partial\Omega)} &\leq C U^{1-\lambda-\mu} L^{\lambda-1/2} \|u\|_{L^{2}(\Omega)}^{\lambda} \left[ L^{2}\|u\|_{L^{2}(\Omega)}^{2} + |u|_{W^{1,2}(\Omega)}^{2} \right]^{\mu/2}\\ &\leq CU^{1-\lambda-\mu} L^{\lambda-1/2} \|u\|_{L^{2}(\Omega)}^{\lambda} \left[ L^{\mu}\|u\|_{L^{2}(\Omega)}^{\mu} + |u|_{W^{1,2}(\Omega)}^{\mu} \right] \end{align*} \] Since \(U,L\) are arbitrary, there should be \(\lambda+\mu=1\) and \(\lambda \leq 1/2\). \(\heartsuit\)
参考
- Monk, P. (2003). Finite Element Methods for Maxwell’s Equations. In Numerical Mathematics and Scientific Computation.
- Brenner, S. C., & Scott, L. R. (2008). The Mathematical Theory of Finite Element Methods (Third).
- Inf-sup 条件. 数值分析大巴.