插值方法的基本概述和讨论

插值方法是数值计算和模拟中使用的基本方法, 在许多现实问题中具有重要应用. 在本文中我们给出了几种插值方法的应用示例, 并对各种插值方法进行了概述和总结.

预备知识

• 了解数值微分的基本内容
• 了解基本插值方法的定义和用法

为什么需要插值

给定 \(n+1\) 个离散点:\[ (x_0,y_0), (x_1,y_1), \ldots, (x_n,y_n).\]我们希望求 \(\hat{x}\) 对应的值 \(\hat{y}\). 或者估计某个点 \(x_k\) 处的 “导数”.

科学家生活中的一个重要部分是对测量数据的解释或理论计算. 通常当你做测量时, 你会有一组离散的点来代表你的实验. 为了简单起见, 我们假设你的实验用一对数值来表示: 一个自变量 “x” (你可以改变它) 和一个量 “y” (在x点的测量值). 作为说明, 考虑一个放射源和一个计算衰变次数的探测器. 为了确定这个源的半衰期, 你可以计算在时间点 \(t_0, t_1, \ldots, t_k\) 的衰变数量 \(N_0, N_1, N_2，\ldots, N_k\). 在这种情况下, \(t\) 是独立的自变量, 以最适合问题的方式来选择它. 然而, 您测量的是在 \([t_0, t_k]\) 范围内的一组离散的数字 \((t_k, N_k)\). 为了从这样的实验中提取信息, 我们希望能够找到一个解析函数它能给出任意点 \(t\) 的值 \(N\). 但是, 有时试图找到一个解析函数是不可能的, 或者即使解析函数已知, 但计算太耗时了, 或者我们可能只对自变量的某个局部区域感兴趣.

为了说明这一点，假设你的辐射源是 241Am，一个 \(\alpha\)-辐射体. 其半衰期 \(\tau_{1/2}=430\). 显然你不能通过完整的测量来确定它的半衰期. 因为它是非常缓慢的衰变, 你可能会在一段较长的时间内测量一下, 比如几个月的每个周一. 五个月后, 你会停下来看看数据. 你们可能想要回答的一个问题是第三周周三的活动是什么? 因为这一天在您的 \([t_0, t_k]\) 范围内, 您可以使用插值方法来确定这个值. 另一方面, 如果您想知道在测量结束后 8 个月的活动, 您可以从之前的一系列测量中推断出这一点. 插值的思想是选择一个函数 \(f(x)\) 对于每个数据点都有 \(f(x_i)= y_i\), 这个函数是原始数据点之间任意 \(\hat{x}\) 的一个很好的近似. [2]

应用示例

人口问题

下面的表格中的数据是新中国成立以来的历次人口普查结果, 但是七十年代没有数据, 如何根据已知的年份数据进行估计呢? 如何对 2030 年的人口进行预测?

	第一次	第二次	第三次	第四次	第五次	第六次	第七次
年份	1953	1964	1982	1990	2000	2010	2020
人口(万)	59,435	69,458	100,818	113,368	126,583	133,972	141,178

这个问题是插值方法的典型应用领域,我们可以利用经典的 Lagrange 插值或差商方法来求得 1970 或 2030 年的近似人口数.

桥梁损伤测定

在桥梁结构损伤分析中, 传感器不可能设置在每个节点上, 因此需要利用插值技术将测试数据扩展到每个需要的节点 [1].

加速度问题

给定一系列速度的测量值, 估计加速度的变化情况. 例如, 根据下表估计时间 \(15\) 时的加速度.

时间(s)	5	10	15	20	30	50
速度(m/s)	20	30	25	12	40	50

我们知道加速度是速度关于时间的导数. 因为我们是无法对一组离散点进行求导的, 但是一个简单的做法是利用插值来得到一个代表速度的多项式, 然后我们再对这个多项式进行求导, 最后代入时间点 15 得到近似的加速度.

湖泊温跃层处的热通量

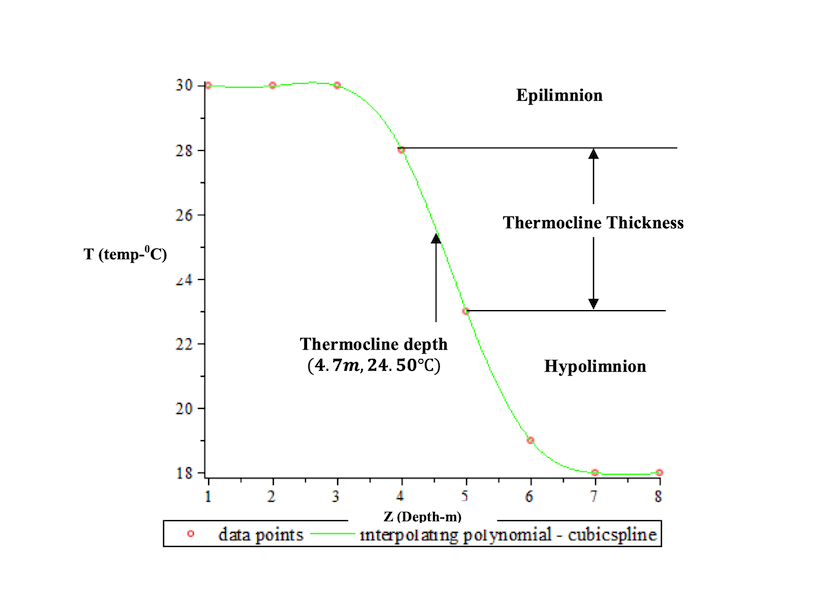
温跃层是大量流体（例如水，如海洋或湖泊，或空气，如大气）中的薄而独特的层, 其中温度随深度变化的速度比它上层或下层更快. 根据傅立叶热传导定律，热量从高温区域流向低温区域. 对于一维情况，这可以在数学上表示为 \(q=-k \frac{\partial T}{\partial z} \), 其中 \(q\) 为热通量 (heat flux), \(T\) 为温度, \(z\) 表示深度, \(k\) 表示热传导系数. 下表中, 我们从湖泊中收集了每个深度为 1m 至 8m 的八个温度值 [4]:

深度(m)	1	2	3	4	5	6	7	8
温度(\(^\circ\)C)	30	30	30	28	23	19	18	18

如果我们根据这些离散点得到一个插值多项式函数或者三次样条函数 \(P(x)\), 它就是温度-深度变化关系的一个近似. 由物理常识我们知道, 温跃层深度的位置就是温度-深度曲线的拐点, 即 \(\frac{\partial^2 T}{\partial z^2}=0 \). 求解上面的方程, 我们可以得到温跃层的近似深度 \(\hat{z}\), 并且根据傅立叶热传导定律求得温跃层附近的热通量 \(q=-k \frac{\partial P}{\partial z}(\hat{z}) \). 例如, 下面的图中展示了三次样条插值 (自然边界条件) 多项式的图像.

PM2.5 模型的初值条件

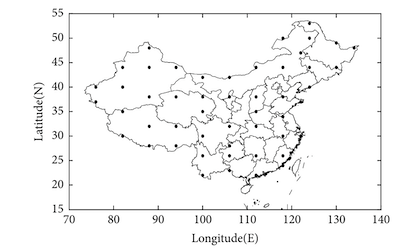
PM2.5的传输模型的求解需要足够充分的初值条件, 但是实际检测的数据是分布在平面上的离散点, 如下图所示. 其中一种方法就是采用平面样条插值 (Surface spline interpolation) [5].

其它应用

如样条插值在损伤认定中的应用 [6], 三维插值在中国南海海洋扩散率估计中的应用 [7] 等等.

关于插值的一些讨论

最基础也是最容易理解的插值方法是 Lagrange 插值 (具体算法可以参考: [8, 9, 10]), 也就是利用 \(n+1\) 个点来构造一个 \(n\) 阶多项式, 使得对所有的离散点精确成立. 这个方法的优点是思想简单, 操作容易, 是最常用的方法. 另外, 如果我们只想得到某个或某几个缺失的数据而不想显示地求出插值多项式, 那么可以选择更为便捷的 Neville 方法. 除了直接得到多项式表达式的 Lagrange 插值之外, 还有一种采用迭代的特价的办法—-差商法 (Divided difference). 这些方法的本质其实就是通过离散点来构造 \(n\) 阶多项式, 得到缺失的数据的一个近似.

通常来说, 如果我们知道解析函数 \(f(x)\), 插值对应的误差有如下表达式\[ f(x)-P_n(x) = \frac{(x-x_0)\cdots(x-x_n)}{(n+1)!}f^{(n+1)}(\xi), \quad \exists \xi\in (x_0, x_n).\]这个先验误差估计说明了对任一个光滑函数 (至少 \(n+1\) 阶导数存在), 它与插值多项式之间的误差随多项式阶数的增加而减小. 但是, 光滑性要求在许多工程应用中是不现实的. 一个很简单的例子是对函数 \(1/(1+x^2)\) 的插值近似 [3]. 下图 (左) 中显示了函数 \(1/(1+x^2)\) 与其八次插值函数在区间 \([-5,5]\) 上的图像, 其中插值点等距分布. 可以明显看出误差主要集中在区间的两端. 为了减小误差, 最直观的方法就是通过增加离散点的个数, 但是这只会导致更加糟糕的结果! 我们在右图画出了对应的 \(30\) 阶多项式, 误差并没有像我们预期的那样减小, 反而剧烈地增大了! 这种现象首先由数学家 Runge 发现, 所以称为 Runge 现象.

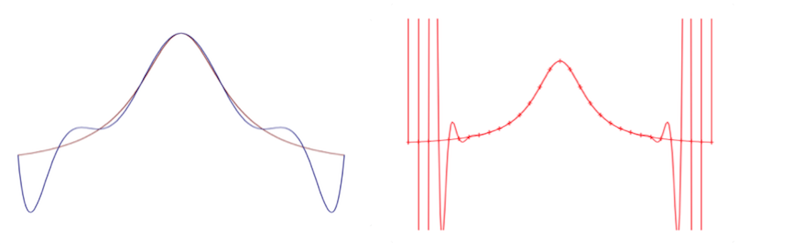
上述例子告诉我们, 单纯地通过增加多项式的次数并不一定能达到减小误差的目的, 尤其是当函数达不到足够光滑的时候. 所以, 这种使用全局多项式的做法并不是在所有情况下都可取的, 相反地, 分片多项式插值 (Piecewise polynomial interpolation)—-构造分片连续的插值多项式—-成为相对优越的选择. 全局和分片多项式插值有着极大的不同. 首先, 由于 Runge 现象的存在 (其实它有着深刻的数学原因), 高阶多项式的误差在某个有限区间上变得异常巨大, 从而导致插值结果不可用; 分片插值并不存在这个问题. 其次, 全局插值得到的高阶多项式会导致更高的计算复杂度, 达到 \(O(n^2)\), 而分片插值的复杂度可以保持线性增长.

最容易想到的方法就是采用分片线性插值, 即用直线将所有离散点依次连接起来. 如果我们这样做, 就得到了一个在结点处无法微分的函数, 也就是说这个函数是“不光滑”的, 这样的话许多应用中 (如求加速度的例子) 无法使用的. 这个问题也启发我们需要找一个可微的分片插值多项式. 一个可行的做法当然是利用 Hermite 插值 (参考: [8, 9, 10]) 得到一个全局可微的多项式, 并且这个多项式在所有结点上的函数值和导数值都与原函数相同. 但是, 我们知道 Hermite 插值的构造需要知道被近似函数在离散点处的导数值, 通常在物理应用是不现实的. 那么有没有一种不需要知道原函数的导数值就可以构造光滑分片多项式的方法呢?

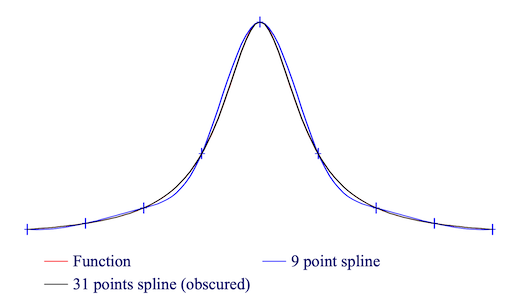
答案是有的, 最为熟知的就是三次样条插值 (Cubic Splines). 简单用数学语言来说, 它是一个在每个小区间上是三次多项式并且其一阶导数和二阶导数在所有内部结点上都连续的分片多项式. 因为三次样条插值具有很自然的物理背景, 所以对土木工程师来说它是工程应用中非常自然的一种插值方法, 关于它的一般定义可以参考任意数值分析教材. 下面的图可以表明样条插值在拟合非光滑函数方面的优势 [3], 其中相比于 9 点, 31 个点的插值多项式因为误差更小, 基本和原函数重合, 避免了全局多项式插值产生 Runge 现象. 这里需要注意的是, 虽然全局 Lagrange 插值会产生诸如 Runge 现象和增加计算复杂度的缺点, 但是当我们处理低阶问题时, 它还是会因为计算简单而被大家喜欢.

总结

插值方法没有最优, 只有更优. 在实际应用中, 我们必须根据需要来确定要使用的插值方法, 有时数据拟合可能是更好的选择. 另外, 插值方法也在不断发展, 其应用领域也在不断增加, 因此笔者由衷地希望有兴趣的读者可以在将来对这一领域有所发展, 有所贡献.

参考

[1] APPLICATION OF INTERPOLATION IN CIVIL ENGINEERING.
[2] Vinamrita Singh. Interpolation/Extrapolation and Its Application to Solar Cells.
[3] John D. Fenton. Interpolation and numerical differentiation in civil engineering problems. Civil Engng Transactions. 1994.
[4] C.R. Chikwendu, etc. An Application of Spline and Piecewise Interpolation to Heat Transfer (Cubic Case). Mathematical Theory and Modeling. 2015.
[5] Ning Li, Xianqing Lv, Jicai Zhang, Application of Surface Spline Interpolation Method in Parameter Estimation of a PM2.5 Transport Adjoint Model, Mathematical Problems in Engineering, 2018.
[6] Pedroso, L, Arco, A, Figueiras, I, Araújo dos Santos, JV, Fernandes, JLM, Lopes, H. Application of cubic spline interpolation with optimal spatial sampling for damage identification. Struct Control Health Monit. 2021.
[7] Guo, J.; Nie, Y.; Li, S.; Lv, X. Application of Three-Dimensional Interpolation in Estimating Diapycnal Diffusivity in the South China Sea. J. Mar. Sci. Eng. 2020.
[8] Burden, R. L., & Faires, J. D. (2010). Numerical Analysis. In Cengage Learning (9th ed.).
[9] 李庆扬. (2008). 数值分析(第五版). 清华大学出版社.
[10] 关治, 陆金甫. (1998). 数值分析基础. 高等教育出版社.

---