重心坐标及其应用
定义
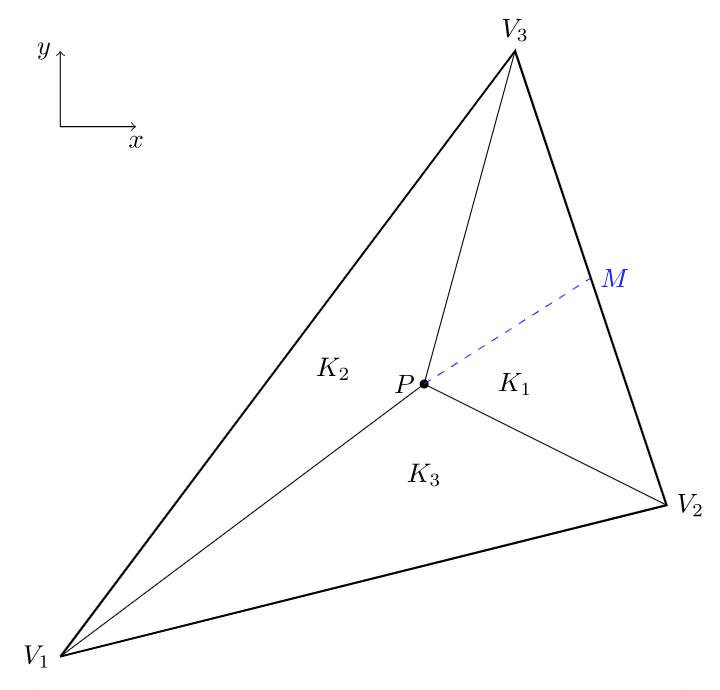
考虑三角形 \(K\) 的三个顶点 \(V_1, V_2, V_3\) 的坐标为\[ \mathbf{v}_1=\begin{bmatrix} x_0 \\ y_0 \end{bmatrix},\quad \mathbf{v}_2=\begin{bmatrix} x_1 \\ y_1 \end{bmatrix},\quad \mathbf{v}_3=\begin{bmatrix} x_2 \\ y_2 \end{bmatrix}.\]如下图所示, 点 \(P\) 是子三角形 \(K_1, K_2, K_3\) 的共同顶点, 坐标记为 \(\mathbf{p}=\begin{bmatrix} x \\ y \end{bmatrix}\). 令 \(|K|\) 为三角形 \(K\) 的面积.
定义 1. 令 \(\lambda_1, \lambda_2, \lambda_3\) 为三角形内动点 \(P\) 的重心坐标 (函数), 定义如下\[ \lambda_i(P) : = \frac{|K_i|}{|K|}. \tag{1}\]可以看出, \(\lambda_i=\lambda_i(x,y)\) 依赖于点 \(P\) 的坐标 \(\mathbf{p}\), 并且满足\[ \lambda_1+\lambda_2+\lambda_3\equiv 1,\quad \lambda_i(V_j)=\begin{cases} 1 & \text{for } i=j,\\ 0 & \text{for }i\neq j. \end{cases} \tag{2}\]
注 1. 由笛卡尔坐标中的三角形面积公式\[ |K| = \frac{1}{2}\left| \begin{matrix} 1 & x_0 & y_0 \\ 1 & x_1 & y_1 \\ 1 & x_2 & y_2 \end{matrix} \right| = \frac{1}{2} \left| \begin{bmatrix} x_0\\ x_1 \\ x_2 \end{bmatrix} \times \begin{bmatrix} y_0\\ y_1 \\ y_2 \end{bmatrix} \right|, \quad |K_i| = \frac{1}{2}\left| \begin{matrix} 1 & x & y \\ 1 & x_{i+1} & y_{i+1} \\ 1 & x_{i+2} & y_{i+2} \end{matrix} \right|, \tag{3}\]其中, \(i+1, i+2\) 为循环角标, 即 \(i+1 \to (i+1)\%3\). 例如, \(i=2\) 可得 \(i+2 \to (i+2)\%3=1\). 由 (3) 可以看出重心坐标 \(\lambda_i\) 是关于 \(x\) 和 \(y\) 的线性函数, 具有形式 \(\lambda_i = a_i + b_i x+ c_i y\). 三个重心坐标函数如下图所示.

引理 1 (重心坐标的梯度). 令 \(\lambda_i\) 为三角形 \(K\) 上的重心坐标, \(e_i\) 为顶点 \(V_i\) 的对边, \(\mathbf{n}_i\) 为外法向量, 那么\[ \nabla \lambda_i = -\frac{|e_i|}{2|K|} \mathbf{n}_i. \tag{4}\]
证明. 容易得出, 外法向量 \(\mathbf{n}_i=\frac{1}{|e_i|}\begin{bmatrix} y_{i+2}-y_{i+1} \\ -(x_{i+2}-x_{i+1}) \end{bmatrix}\). 将 (3) 中行列式展开并求梯度, 可得\[ \nabla \lambda_i = – \frac{1}{2|K|} \begin{bmatrix} y_{i+2}-y_{i+1} \\ -(x_{i+2}-x_{i+1}) \end{bmatrix} = -\frac{|e_i|}{2|K|} \mathbf{n}_i.\]
引理 2. 三角单元上任意点 \(P\) (坐标为 \(\mathbf{p}\)) 具有如下的重心坐标形式:\[ \mathbf{p}=\lambda_1 \mathbf{v}_1+\lambda_2 \mathbf{v}_2 + \lambda_3 \mathbf{v}_3. \tag{5}\]相反, 任一组重心坐标 \((\lambda_1, \lambda_2, \lambda_3)\) 也对应一个点 \(P\).
证明. 如图所示, 通过延长线段 \(V_1P\) 交线段 \(V_2V_3\) 于点 \(M\), 坐标记为 \(\mathbf{m}\). 容易看出,\[ \frac{|V_2M|}{|MV_3|}=\frac{\lambda_3}{\lambda_2} \quad \Rightarrow \quad \mathbf{m} = \frac{\lambda_2}{\lambda_2+\lambda_3} \mathbf{v}_2 + \frac{\lambda_3}{\lambda_2+\lambda_3} \mathbf{v}_3.\]类似地, 我们有\[ \frac{|V_1P|}{|PM|}=\frac{\lambda_2+\lambda_3}{\lambda_1} \quad \Rightarrow \quad \mathbf{p} = \frac{\lambda_1}{\lambda_1+\lambda_2+\lambda_3} \mathbf{v}_1 + \frac{\lambda_2+\lambda_3}{\lambda_1+\lambda_2+\lambda_3} \mathbf{m}.\]注意到 \(\lambda_1+\lambda_2+\lambda_3\equiv 1\) 并利用 \(\mathbf{m}\) 的表达式, 可得 (5). \(\heartsuit\)
注 2. 四面体是三维空间中的单纯形, 相当于二维空间中的三角形, 类似地, 也有重心坐标的概念. 考虑四面体的四个顶点, 坐标为 \(\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3, \mathbf{v}_4\), 那么存在重心坐标 \(\lambda_i\) 对应一点 \(\mathbf{p}\):\[ \mathbf{p} = \sum_{i=1}^4 \lambda_i \mathbf{v}_i \quad \text{其中 } \sum_{i=1}^4 \lambda_i \equiv 1.\]其中,\[ \lambda_i = \frac{|K_i|}{|K|},\quad |K| = \frac{1}{6}\left| \begin{matrix} 1 & x_0 & y_0 & z_0 \\ 1 & x_1 & y_1 & z_1 \\ 1 & x_2 & y_2 & z_2 \\ 1 & x_3 & y_3 & z_3 \end{matrix} \right| = \frac{1}{6} |\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c}) |.\]

应用
数值积分
三角单元上的数值积分法则有时以重心坐标的形式给出, 避免了向参考单元变换的过程. 例如, 下面是一阶和二阶精度的积分法则 (更多积分法则参考二维数值积分):
| n | 权重 | \lambda_1 | \lambda_2 | \lambda_3 |
| 1 | .3333333333333333 |.3333333333333333 | .3333333333333333 | .3333333333333333 |
| 2 | .3333333333333333 |.1666666666666666 | .1666666666666667 | .66666666666666667 |
| | .3333333333333333 |.1666666666666666 | .6666666666666667 | .16666666666666666 |
| | .3333333333333333 |.6666666666666666 | .1666666666666667 | .16666666666666666 |令三角单元 \(K\) 的三个顶点坐标为 \((x_0,y_0), (x_1,y_1), (x_2,y_2)\). 那么由重心坐标积分法则 \((w_i; \lambda_1^{(i)}, \lambda_2^{(i)},\lambda_3^{(i)})\), \(i=0,1,\ldots, n-1\), 可以计算数值积分\[ \int_K f(x,y)dK \approx |K| \sum_{i=0}^{n-1} w_i f(\bar{x}_i, \bar{y}_i).\tag{6}\]其中, \((\bar{x}_i, \bar{y}_i)\) 为单元 \(K\) 上的积分点, 定义如下\[ \begin{bmatrix} \bar{x}_i \\ \bar{y}_i \end{bmatrix} = \begin{bmatrix} x_0 & x_1 & x_2 \\ y_0 & y_1 & y_2 \end{bmatrix} \begin{bmatrix} \lambda^{(i)}_1 \\ \lambda^{(i)}_2 \\ \lambda^{(i)}_3 \end{bmatrix}.\]
线性有限元空间
引理 3. 三角形单元上的重心坐标函数 \(\lambda_i\), \(i=1,2,3\) 构成了线性 (一阶) 多项式空间的一组基:\[ \mathbb{P}_1(K):=\text{span}\left\{ 1,x,y \right\}=\text{span}\left\{ \lambda_1, \lambda_2, \lambda_3 \right\}.\]
证明. 只需要说明 \(\lambda_i\) 是线性无关的. 假设\[ 0=\alpha_1 \lambda_1 + \alpha_2 \lambda_2 + \alpha_3 \lambda_3,\]代入顶点 \(V_1\) 的坐标, 由定义 (2) 可知, \(0=\alpha_1 \lambda_1(\mathbf{v}_1)=\alpha_1\). 类似地, 我们有 \(\alpha_2=\alpha_3=0\). \(\heartsuit\)
我们可以利用如下的方法求解重心坐标的具体表达式, 这个过程也是有限元编程的一个实现过程. 具体地, 假设\[ \lambda_i(x,y)= a_i+b_i x+c_i y,\quad i=1,2,3.\]其中, \(a_i,b_i,c_i\) 是未知的多项式系数. 由重心坐标的定义 (2) 可知它们满足如下矩阵方程\[ \begin{bmatrix} 1 & x_0 & y_0 \\ 1 & x_1 & y_1 \\ 1 & x_2 & y_2 \end{bmatrix}\begin{bmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}. \tag{7}\]因为系数矩阵是非奇异的, 上面的矩阵方程总是有唯一解.
一阶棱元 (edge element)
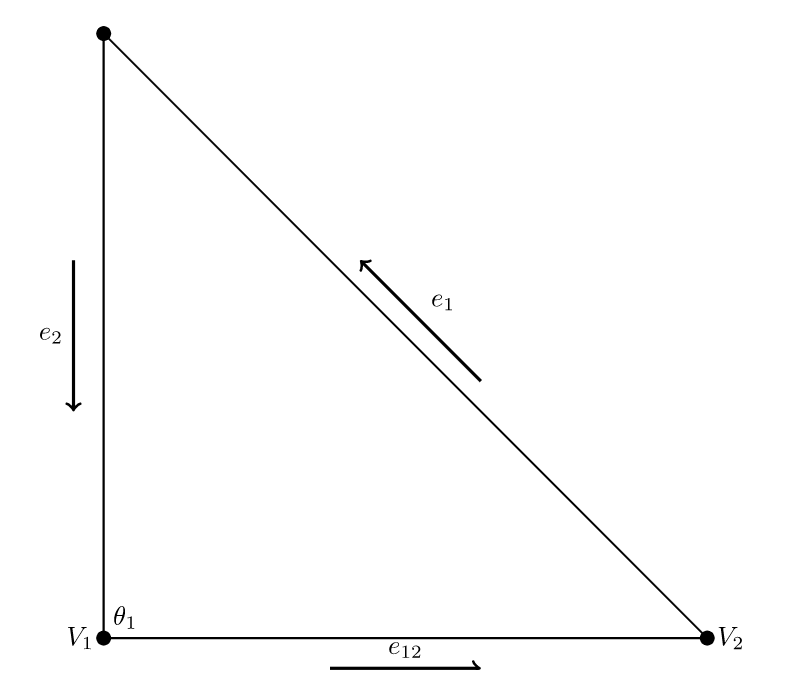
一阶棱元又称为 Whitney 元, 是用来离散 Maxwell 方程最常用的最低阶有限元, 因为其自由度定义在三角形的边上或四面体的棱上, 所以常常称为棱元. 二维情况下, 可以定义为如下向量多项式空间\[ R_1(K):= \left\{ a+\mathbf{b}\times \mathbf{x} \right\},\]其中, \(a\) 是常数, \(\mathbf{b}\) 是二维常向量, \(\mathbf{b}\times \mathbf{x}:=b_1 y-b_2 x\). 自由度有三个, 它们分别对应于三角形的三条边. 可以证明 \(R_1(K)\) 的一组基如下\[ R_1(K)=\text{span}\left\{ \psi_{12}, \psi_{23}, \psi_{31}\ |\ \psi_{ij}=\lambda_i \nabla \lambda_j- \lambda_j \nabla \lambda_i \right\}.\]
引理 4. 如果令 \(e_{ij}\) 为连接顶点 \(V_i\) 和 \(V_j\) 构成的边, 其切向量为 \(\tau_{ij}\), 那么直接计算可得\[ \int_{e_{ij}} \psi_{ij}\cdot \tau_{ij}ds=1. \tag{8}\]
事实上, 我们可以给出 \(\psi_{12}\) 的证明. 显然, \(\psi_{12}\) 是一个线性函数, 所以利用中点积分法则 (\(M\) 为中点)\[ \int_{e_{12}} \psi_{12}\cdot \tau_{12}ds = |e_{12}| \psi_{12}(M)\cdot \tau_{12}.\]然后, 利用 \(\lambda_1, \lambda_2\) 在中点处为 \(\frac{1}{2}\) 和 (4) 中关于梯度的表达式, 可以得到\[ \begin{align*} \psi_{12}(M)\cdot \tau_{12} &= – \frac{1}{2} \frac{1}{2|K|} \left( |e_2|\mathbf{n}_2 \cdot \tau_{12} – |e_1|\mathbf{n}_1 \cdot \tau_{12} \right) \\ &= – \frac{1}{4|K|} \left( -|e_2|\sin \theta_1 – |e_1| \sin \theta_2 \right) \\ &= – \frac{1}{4|K|} \left( -h – h \right) = \frac{1}{2|K|} h, \end{align*}\]其中, \(\theta_1, \theta_2\) 分别为顶点 \(V_1,V_2\) 对应的内角, \(h\) 是边 \(e_{12}\) 对应的三角形的高. 整理可得\[ \int_{e_{12}} \psi_{12}\cdot \tau_{12}ds = \frac{1}{|K|} \frac{1}{2} |e_{12}| h = 1.\]其它两个基函数可以类似证明. \(\heartsuit\)
附录: 叉乘
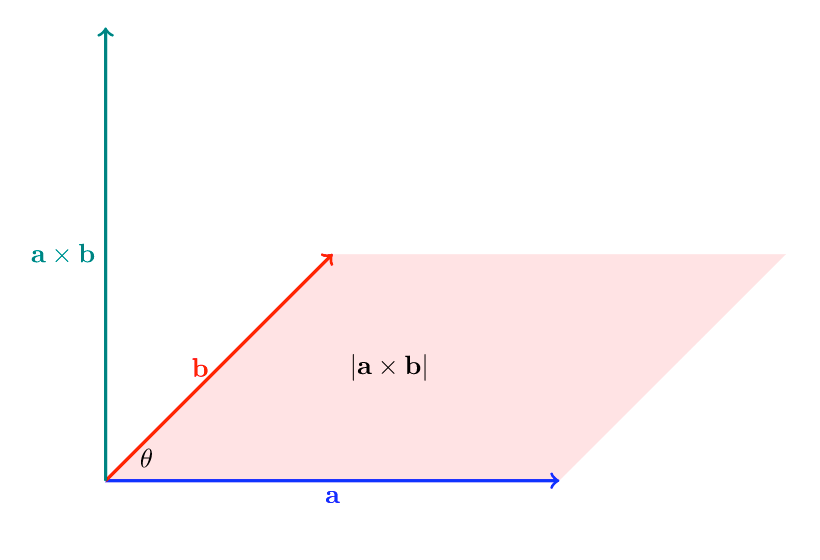
给定向量\[ \mathbf{a}=\begin{bmatrix} a_1\\ a_2 \\ a_3 \end{bmatrix}, \quad \mathbf{b}=\begin{bmatrix} b_1\\ b_2 \\ b_3 \end{bmatrix},\]其叉乘可以定义如下\[ \mathbf{a}\times \mathbf{b} = \begin{bmatrix} \ a_2b_3-a_3b_2 \\ -(a_1b_3-a_3b_1) \\ \ a_1b_2-a_2b_1 \end{bmatrix},\]并且叉乘的模满足 \(|\mathbf{a}\times \mathbf{b}|= |\mathbf{a}||\mathbf{b}| \sin \theta\), 其中 \(\theta\) 为两个向量的夹角. 容易看出, 叉乘的模就是两向量构成的平行四边形的面积.