二维数值积分
数值积分是有限元编程中必不可少的一环. 根据网格的不同, 我们需要在三角形, 矩形或者多边形等有限元单元上进行数值积分. 根据有限元空间选取的不同, 我们必须提供足够精确的数值积分法则, 从而保证有限元方法的最优收敛性. 数值积分不仅可以应用于有限元方法, 还被广泛应用于工程领域, 如冶金能源, 水利工程, 核技术, 计算物理等等 (参考 [1-5]).
简介
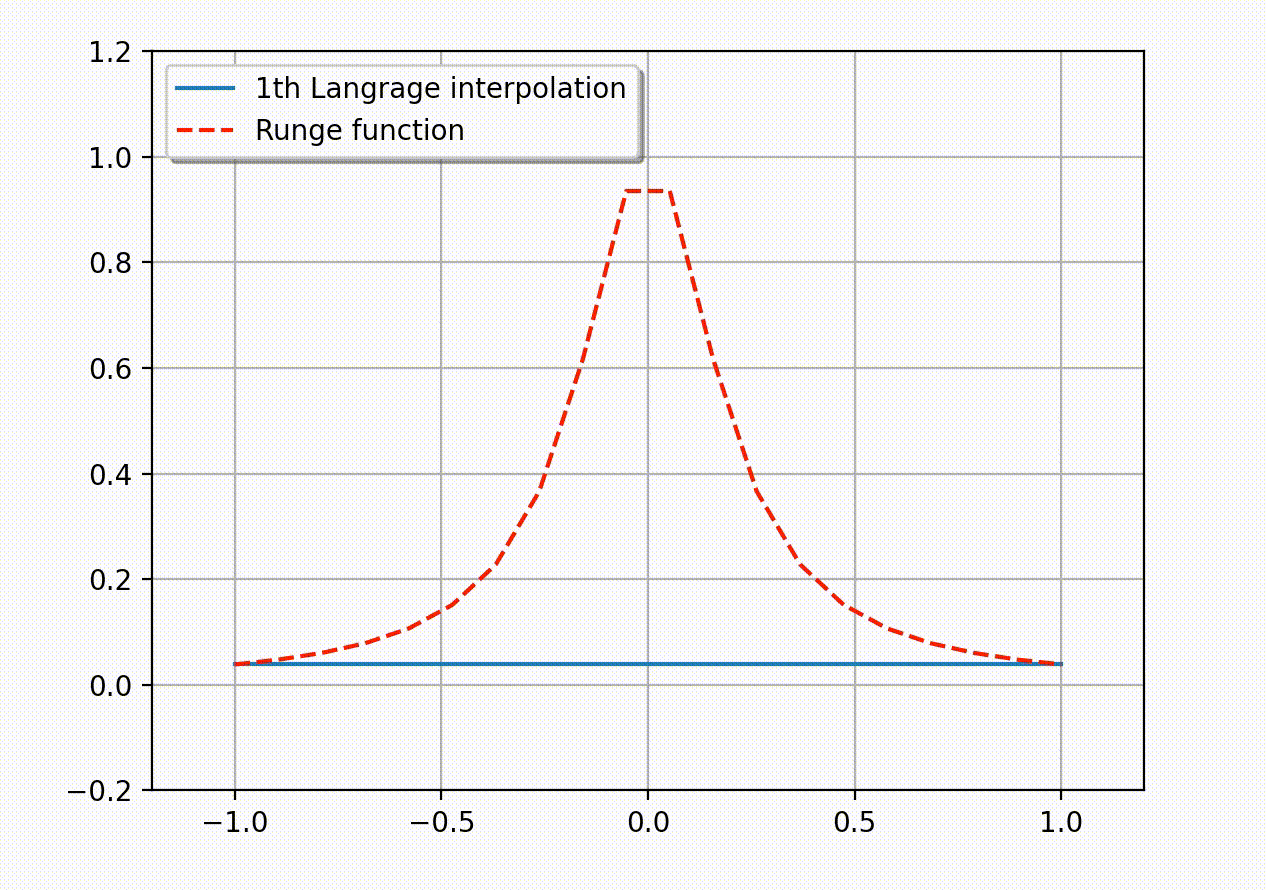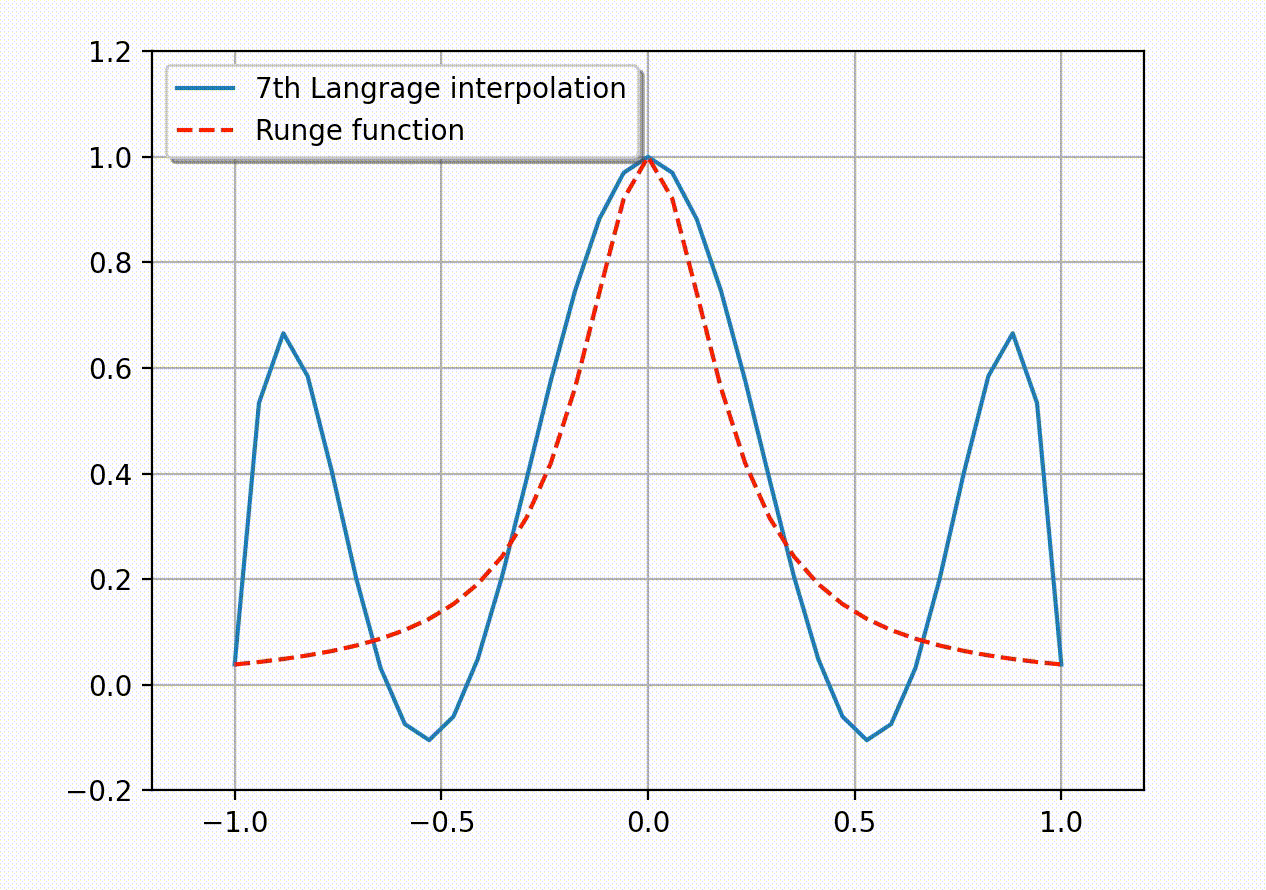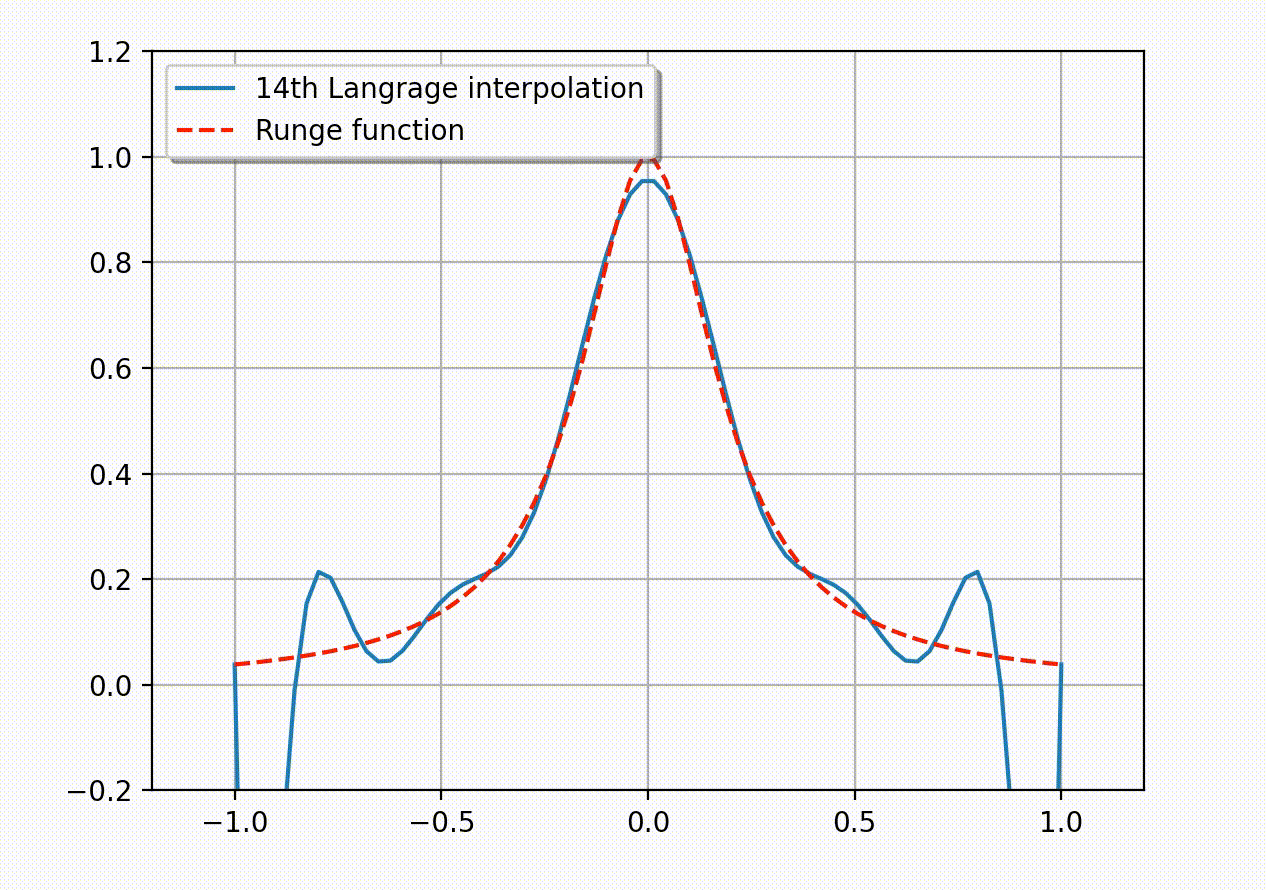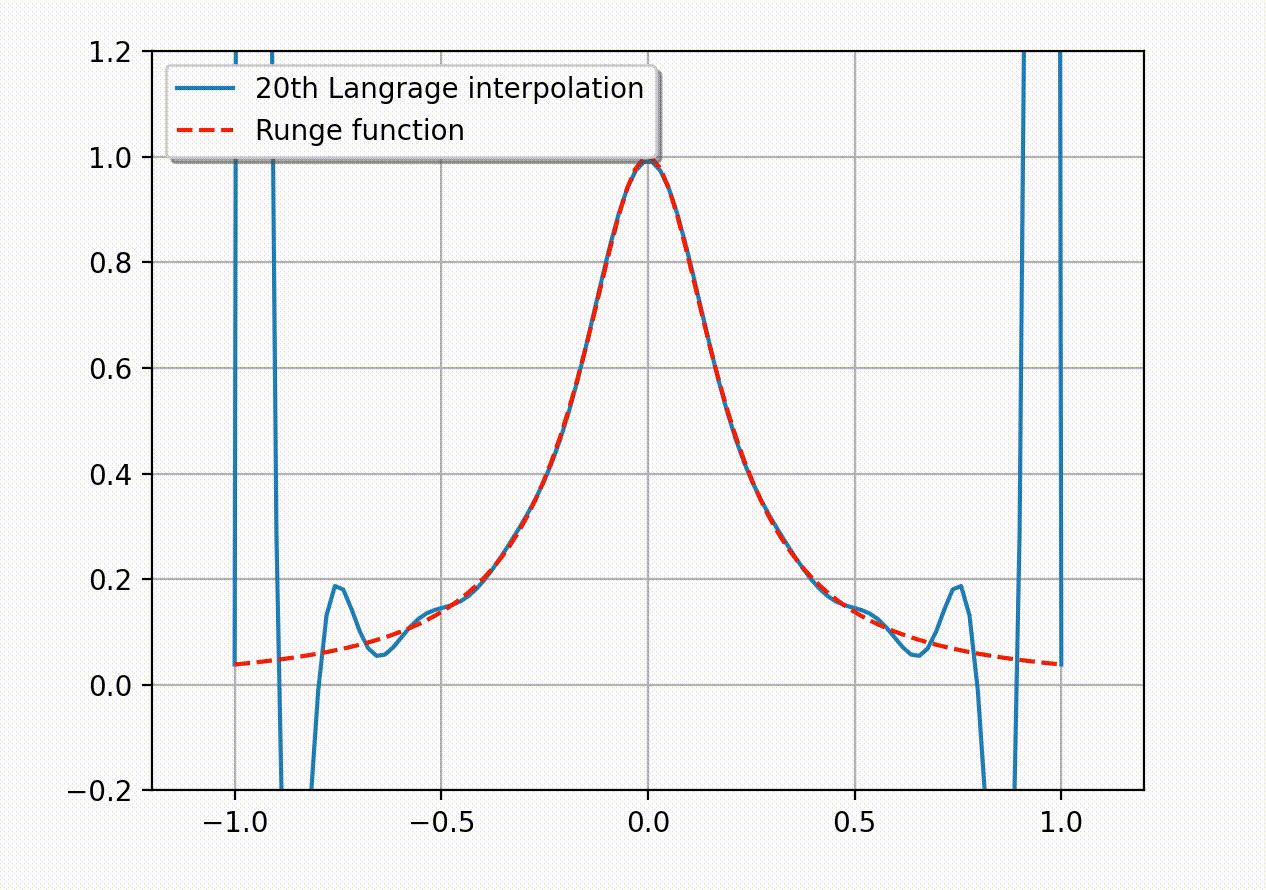
数值积分是一种近似计算定积分的数值方法, 一般表示为函数在积分区域上的某些点的加权和. 具体地, 数值积分是定积分的一个近似 \begin{equation}\tag{Eq. 1} \int_K f(x,y)dK \approx \sum_{i=1}^n \omega_i f(x_i, y_i), \end{equation} 这里 \(\omega_i\) 称为积分权重, \((x_i, y_i)\in \overline{K}\) 为积分点, 它们一起被称为积分法则. 我们定义区域 \(K\) 上的 \(k(\geq 0)\) 次多项式函数空间如下 $$ \mathbb{P}_k(K):=\text{span}\{ x^my^n: 0\leq m,n\leq k\ \text{且}\ m+n\leq k\}. $$ 如果一个积分法则 \((\omega_i; x_i,y_i)\) 使 ( Eq. 1) 对所有 \(k\) 次多项式函数严格成立, 那么我们称积分法则具有 \(k\)-阶数值精度.
三角单元积分
三角形 \(K=[(x_0,y_0), (x_1,y_1), (x_2,y_2)]\) (逆时针顺序) 上的积分一般变换到参考单元上计算. 令 \(\hat{K}\) 为参考单元, \((0,0),(1,0),(0,1)\) 分别为它的三个顶点. 作如下仿射变换 \(F:\hat{K}\to K\): \begin{equation*} K\ni (x,y) = F(s,t) =\begin{bmatrix}x_0\\ y_0 \end{bmatrix} + \begin{bmatrix}x_1-x_0,\ x_2-x_0\\ y_1-y_0,\ y_2-y_0 \end{bmatrix} \begin{bmatrix}s\\ t \end{bmatrix}, \quad \forall (s,t)\in \hat{K}. \end{equation*} 因此, \begin{equation}\begin{split} \int_K f(x,y) \mathrm{d}x\mathrm{d}y &=\int_{\hat{K}}f(F(s,t))\ \mathrm{det}(J_F)\ \mathrm{d}s\mathrm{d}t \\ &\approx 2 |K| \sum_{i=0}^{n-1} \omega_i f(F(s_i,t_i)),\end{split} \tag{Eq. 2} \end{equation} 这里 \(J_F=\begin{bmatrix}x_1-x_0,\ x_2-x_0\\ y_1-y_0,\ y_2-y_0 \end{bmatrix}\) 表示仿射变换 \(F\) 的 Jacobi 矩阵, \(|K|\) 表示三角形的面积, 最后一步用到一个公式 \begin{equation}\tag{Eq. 3} |\mathrm{det}(J_F)| = 2 |K|. \end{equation}
矩形单元积分
矩形区域 \(K=[x_0, x_1]\times [y_0,y_1]\) 上的积分, 一般利用一维的 Gauss 积分来计算. 首先, 假设 \((\omega_i, t_i),\ i=0, 1, \ldots, n-1\) 为 \([-1,1]\) 上的积分法则. 令 $$ x(s)=\frac{x_0+x_1}{2}+\frac{x_1-x_0}{2}s, \quad -1\leq s\leq 1,\\ y(t)=\frac{y_0+y_1}{2}+\frac{y_1-y_0}{2}t, \quad -1\leq t\leq 1, $$ 则 $$ \begin{split} \int_K f(x,y)\mathrm{d}x\mathrm{d}y &= \int_{x_0}^{x_1}\int_{y_0}^{y_1} f(x,y) \mathrm{d}x\mathrm{d}y \\ &= \frac{x_1-x_0}{2} \frac{y_1-y_0}{2} \int_{-1}^{1}\int_{-1}^{1} f(x(s),y(t)) \mathrm{d}s\mathrm{d}t \\ &\approx \frac{x_1-x_0}{2} \frac{y_1-y_0}{2} \sum_{j=0}^{n-1}\sum_{i=0}^{n-1} \omega_i \omega_j f(x(s_i),y(t_j)). \end{split} \tag{Eq. 4} $$
多边形积分
在多边形上数值积分最简单的方法就是将多边形三角化 (Triangulation), 然后在各个三角单元上进行积分.
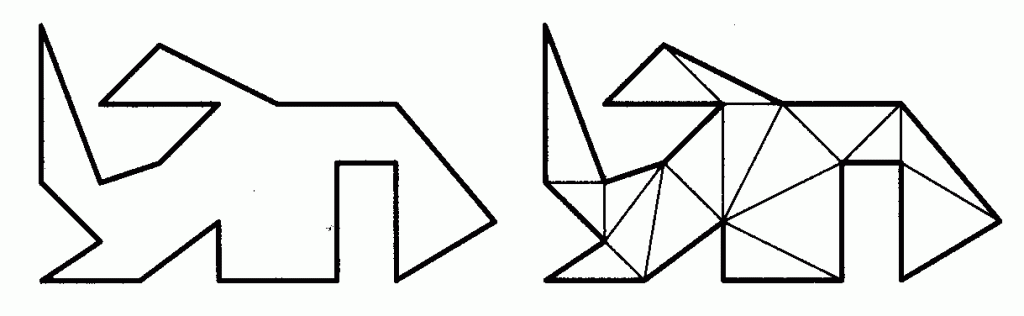
首先, 我们需要找到多边形上的一个三角剖分, 那么对任一个多边形是不是都存在一个三角剖分呢? 下面的定理告诉我们答案是肯定的.
Theorem Every simple polygon admits a triangulation, and any triangulation of a simple polygon with \(n\) vertices consists of exactly \(n-2\) triangles.
(see [7])
实际上, 我们可以利用相关的算法库来实现多边形的三角化, 如 Triangle, 一个用 C 语言编写的开源的三角网格生成库. 它具有生成网格质量高速度快的优点, 另外还有 Python 接口, 使用非常方便. 下面是一个利用 Triangle 的一个例子. 需要注意的是, 利用 Triangle 生成的网格有可能引入新的节点 (不同于多边形的顶点).
import triangle as tr
import matplotlib.pyplot as plt
# Define a polygon by vertices, ordered in counterclockwise
points = np.array([[0.445179, 0.304621],
[0.436864, 0.361401],
[0.380034, 0.403298],
[0.337488, 0.374213],
[0.349248, 0.319155],
[0.404193, 0.276315]])
# Define its boundary edges by using vertex indices in 'points'
seg = np.array([[0, 1],
[1, 2],
[2, 3],
[3, 4],
[4, 5],
[5, 0]])
# Data for using of Triangle
A = dict(vertices=points, segments=seg)
# Generate a triangulation of the polygon
# and the resulting data is stored in
# B['vertices']: all vertices of the triangulation
# B['triangles']: triangles with vertices in B['vertices']
B = tr.triangulate(A, 'pDa')
tr.compare(plt, A, B)
plt.show()
附录 A: 三角形单元积分法则 (重心坐标形式)[9]
| n | 权重 \(\omega_i\) | \(\lambda_1\) | \(\lambda_1\) | \(\lambda_1\) |
| 1 | 1.0 | .3333333333333333 | .3333333333333333 | .3333333333333333 |
| 2 | .3333333333333333 | .1666666666666666 | .1666666666666666 | .6666666666666666 |
| .3333333333333333 | .1666666666666666 | .6666666666666666 | .1666666666666666 | |
| .3333333333333333 | .6666666666666666 | .1666666666666666 | .1666666666666666 | |
| 3 | .2811498024409796 | .1628828503958919 | .1628828503958919 | .6742342992082162 |
| .2811498024409796 | .1628828503958919 | .6742342992082162 | .1628828503958919 | |
| .2811498024409796 | .6742342992082162 | .1628828503958919 | .1628828503958919 | |
| .0521835308923537 | .4779198835675637 | .4779198835675637 | .0441602328648726 | |
| .0521835308923537 | .4779198835675637 | .0441602328648726 | .4779198835675637 | |
| .0521835308923537 | .0441602328648726 | .4779198835675637 | .4779198835675637 | |
| 4 | .2233815896780115 | .4459484909159649 | .4459484909159649 | .1081030181680702 |
| .2233815896780115 | .4459484909159649 | .1081030181680702 | .4459484909159649 | |
| .2233815896780115 | .1081030181680702 | .4459484909159649 | .4459484909159649 | |
| .1099517436553219 | .0915762135097707 | .0915762135097707 | .8168475729804586 | |
| .1099517436553219 | .0915762135097707 | .8168475729804586 | .0915762135097707 | |
| .1099517436553219 | .8168475729804586 | .0915762135097707 | .0915762135097707 | |
| 5 | .225 | .3333333333333333 | .3333333333333333 | .3333333333333333 |
| .1259391805448272 | .1012865073234563 | .1012865073234563 | .7974269853530874 | |
| .1259391805448272 | .1012865073234563 | .7974269853530874 | .1012865073234563 | |
| .1259391805448272 | .7974269853530874 | .1012865073234563 | .1012865073234563 | |
| .1323941527885062 | .4701420641051151 | .4701420641051151 | .0597158717897697 | |
| .1323941527885062 | .4701420641051151 | .0597158717897697 | .4701420641051151 | |
| .1323941527885062 | .0597158717897697 | .4701420641051151 | .4701420641051151 |
为什么考虑重心坐标积分形式? 因为可以避免使用仿射变换, 直接在三角单元上积分.
引理 1. 令三角单元 \(K\) 的三个顶点坐标为 \((x_0,y_0), (x_1,y_1), (x_2,y_2)\). 那么由重心坐标积分法则 \((w_i; \lambda_1^{(i)}, \lambda_2^{(i)},\lambda_3^{(i)})\), \(i=0,1,\ldots, n-1\), 可以计算数值积分\[ \int_K f(x,y)dK \approx |K| \sum_{i=0}^{n-1} w_i f(\bar{x}_i, \bar{y}_i).\tag{5}\]其中, \((\bar{x}_i, \bar{y}_i)\) 为单元 \(K\) 上的积分点, 定义如下\[ \begin{bmatrix} \bar{x}_i \\ \bar{y}_i \end{bmatrix} = \begin{bmatrix} x_0 & x_1 & x_2 \\ y_0 & y_1 & y_2 \end{bmatrix} \begin{bmatrix} \lambda^{(i)}_1 \\ \lambda^{(i)}_2 \\ \lambda^{(i)}_3 \end{bmatrix}.\]
证明. 事实上, 利用仿射变换的 (Eq. 2) 可以写成\[ \int_K f(x,y) \mathrm{d}x\mathrm{d}y \approx |K| \sum_{i=0}^{n-1} 2\omega_i f(F(s_i,t_i)). \tag{6}\]因为仿射变换不改变重心坐标,\[ \begin{bmatrix} x_0 & x_1 & x_2 \\ y_0 & y_1 & y_2 \end{bmatrix} \begin{bmatrix} \lambda_1 \\ \lambda_2 \\ \lambda_3 \end{bmatrix} =\begin{bmatrix} x\\y \end{bmatrix} \quad \overbrace{\Longleftarrow}^{F:\hat{K}\to K} \quad \begin{bmatrix} \hat{x}\\ \hat{y} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \lambda_1 \\ \lambda_2 \\ \lambda_3 \end{bmatrix},\]即 \((x,y)\) 与参考单元上的对应点具有相同的重心坐标. 如果我们知道参考单元 \(\hat{K}\) 上积分点, 其对应的重心坐标就是单元 \(K\) 上的积分点对应的重心坐标, 而权重具有关系 \(w_i=2 \omega_i\) (对比 (5,6) 可知). \(\heartsuit\)
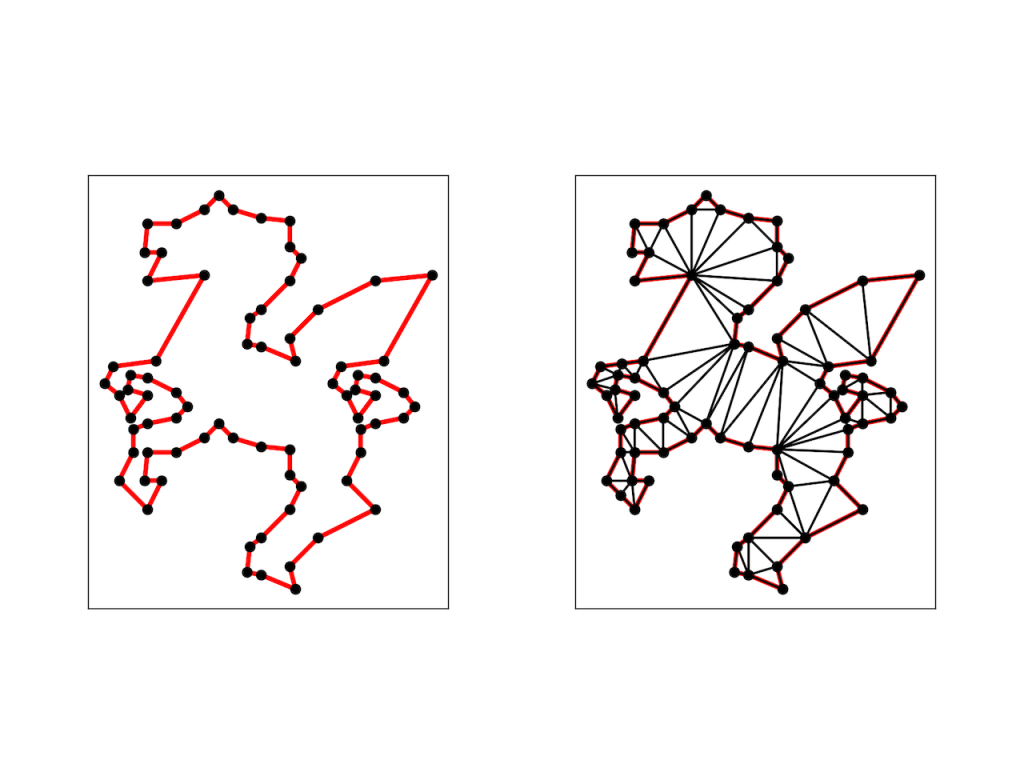
附录 B: 一个有趣的例子
下面的点构成了一个非凸多边形, 有兴趣的读者可以用 Triangle 来生成它的三角剖分.
points = np.array([[ 0. , 0. ],
[ 0.03125, 0.0625 ],
[-0.00625, 0.0625 ],
[ 0. , 0.125 ],
[ 0.0625 , 0.125 ],
[ 0.125 , 0.15625],
[ 0.15625, 0.1875 ],
[ 0.1875 , 0.15625],
[ 0.25 , 0.1375 ],
[ 0.3125 , 0.13125],
[ 0.3125 , 0.075 ],
[ 0.3375 , 0.05 ],
[ 0.3125 , 0. ],
[ 0.25 , -0.0625 ],
[ 0.225 , -0.08125],
[ 0.21875, -0.1375 ],
[ 0.25 , -0.14375],
[ 0.325 , -0.175 ],
[ 0.3125 , -0.125 ],
[ 0.375 , -0.0625 ],
[ 0.5 , 0. ],
[ 0.4375 , 0.0625 ],
[ 0.46875, 0.125 ],
[ 0.46875, 0.175 ],
[ 0.5 , 0.1875 ],
[ 0.5625 , 0.2 ],
[ 0.5875 , 0.225 ],
[ 0.5625 , 0.25625],
[ 0.5 , 0.2875 ],
[ 0.4625 , 0.29375],
[ 0.45625, 0.2625 ],
[ 0.5 , 0.25 ],
[ 0.4625 , 0.2 ],
[ 0.4375 , 0.25 ],
[ 0.40625, 0.275 ],
[ 0.425 , 0.3125 ],
[ 0.51875, 0.325 ],
[ 0.625 , 0.5125 ],
[ 0.5 , 0.5 ],
[ 0.375 , 0.4375 ],
[ 0.3125 , 0.375 ],
[ 0.325 , 0.325 ],
[ 0.25 , 0.35625],
[ 0.21875, 0.3625 ],
[ 0.225 , 0.41875],
[ 0.25 , 0.4375 ],
[ 0.3125 , 0.5 ],
[ 0.3375 , 0.55 ],
[ 0.3125 , 0.575 ],
[ 0.3125 , 0.63125],
[ 0.25 , 0.6375 ],
[ 0.1875 , 0.65625],
[ 0.15625, 0.6875 ],
[ 0.125 , 0.65625],
[ 0.0625 , 0.625 ],
[ 0. , 0.625 ],
[-0.00625, 0.5625 ],
[ 0.03125, 0.5625 ],
[ 0. , 0.5 ],
[ 0.125 , 0.5125 ],
[ 0.01875, 0.325 ],
[-0.075 , 0.3125 ],
[-0.09375, 0.275 ],
[-0.0625 , 0.25 ],
[-0.0375 , 0.2 ],
[ 0. , 0.25 ],
[-0.04375, 0.2625 ],
[-0.0375 , 0.29375],
[ 0. , 0.2875 ],
[ 0.0625 , 0.25625],
[ 0.0875 , 0.225 ],
[ 0.0625 , 0.2 ],
[ 0. , 0.1875 ],
[-0.03125, 0.175 ],
[-0.03125, 0.125 ],
[-0.0625 , 0.0625 ]])
# generate 'seg'
ne = points.shape[0]
seg = np.vstack((np.arange(ne), (np.arange(ne)+1)%ne)).T
参考
[1] 蒋彦军.采用数值重积分法精确求解辊底炉内角系数[J].冶金能源,2019,38(05):31-36.
[2] 简新平.基于数值积分的橡胶坝坝袋曲线计算与绘图程序研究[J].河北工程大学学报(自然科学版),2019,36(04):45-50.
[3] 陈锐,周书民.基于数值积分的核截面在线生成方法研究[J].核技术,2018,41(12):82-86.
[4] 徐建军,史卫东,李兴伟,舒适.块结构自适应网格上任意区域和任意界面的数值积分[J].计算物理,2017,34(01):10-18.
[5] 闫丽娜,王珂,王世恒.基于神经网络的数值积分改进算法[J].应用数学与计算数学学报,2016,30(04):520-525.
[6] Zhang, L., Cui, T., & Liu, H. (2009). A set of symmetric quadrature rules on triangles and tetrahedra. Journal of Computational Mathematics, 27(1), 89–96.
[7] de Berg, M., Cheong, O., van Kreveld, M., & Overmars, M. (2008). Computational Geometry. In Springer Verlag, Heidelberg (Third Edit).
[8] 高斯积分.
[9] L.B. Zhang, Parallel Hierarchical Grid (PHG), src/quad.c.

请问楼主有没有数值积分的程序?
这里涉及的数值积分方法很容易实现, 所以就没有附在文章里. 楼主可以自己尝试编写或者网上查找一下, 谢谢~
楼主你好 权重公式2是错的 方便给一下出处吗?
感谢指正, 已修改. 这里主要参考数据如下(开源, 可下载源文件):
L.B. Zhang, Parallel Hierarchical Grid (PHG), src/quad.c
以及n = 1的权重系数w 应该和其他n统一, 应该为1
感谢指正,已修改