一维波方程的有限差分方法: Neumann 边界条件

2021年11月22日2021年12月10日 numanal 0 个评论 Neumann边界, 有限差分, 波方程

预备知识

一阶、二阶导数的差分格式
波方程的基本知识和应用

一维波方程

我们考虑如下的定义在弦 \(I=[0,L]\) 上的线性波方程:\[\begin{align} \partial_t^2 u &= c^2\partial_x^2 u +f && \text{in } I\times (0,T), \tag{1}\\ u(x,0) &= u_0 && \text{in } I, \\ \partial_t u(x,0)&=u_1 && x\in I, \\ \partial_x u(0,t) &=0 && t\in (0,T], \\ \partial_x u(L,t) &=0 && t\in (0,T], \\\end{align}\]其中, \(L\) 是弦的长度, \(c\) 是波速, \(u_0\) 和 \(u_1\) 为初始条件.

本文是 [1] (一维波方程的有限差分方法) 对 Neumann 边界条件的推广, 所以其中使用的名词和数值格式可能会再次出现, 如有疑惑请查看原文.

有限差分格式

对于内部网格点, \(i=1,2,…,N_x-1\) 和 \(k=1,2,…,N_t-1\), 我们利用如下的二阶差分格式\[ u_i^{k+1} =2u_i^k-u_i^{k-1} + \left( c\frac{\tau}{h} \right)^2 (u_{i+1}^k-2u_i^k+u_{i-1}^k) + \tau^2f(x_i,t_k). \tag{2}\]

初始条件

第一初始条件容易设置如下\[ u_i^0 = u_0(x_i), \quad i=0,1,\cdots,N_x. \tag{3}\]格式 (2) 在时间层 \(k=0\) 时是没有定义的, 但是利用导数的二阶差分格式可以得到\[ \partial_tu(x_i,t_0)\approx \frac{u^{1}_i-u^{-1}_i}{2\tau}, \tag{4}\]即 \(u_i^{-1} = u^{1}_i – 2 \tau \partial_tu(x_i,t_0)\). 将这个表达式代入 (2), \(k=0\), 就可以得到时间层 \(u_i^1, i=1,\ldots,N_x-1\) 满足的方程\[ u_i^{1} =u_i^{0}+\tau \partial_tu(x_i,t_0) + \frac{1}{2}\left( c\frac{\tau}{h} \right)^2 (u_{i+1}^{0}-2u_i^{0}+u_{i-1}^{0}) + \frac{1}{2}\tau^2f(x_i,t_k). \tag{5}\]

边界条件

对 Neumann 边界条件的处理相对 Dirichlet 复杂一些. 首先, 容易看出差分格式 (2) 当 \(i=0,N_x\) 时是没有定义的, 但是利用 \(\partial_xu(0,t)=0\), 我们可以得到一个二阶差分格式\[ \frac{u^k_{-1}-u^{k}_{1}}{2h}=0, \quad \text{i.e.},\quad u^k_{-1}=u^{k}_1. \tag{6}\]代入 (2), \(i=0\) 就可以得到如下等式\[ u_0^{k+1} =2u_0^k-u_0^{k-1} + 2\left( c\frac{\tau}{h} \right)^2 (u_{1}^k-u_0^k) + \tau^2f(x_0,t_k). \tag{7a}\]相同的方法, 当 \(i=N_x\) 时, 我们有\[ u_{N_x}^{k+1} =2u_{N_x}^k-u_{N_x}^{k-1} + 2\left( c\frac{\tau}{h} \right)^2 (u_{N_x-1}^k-u_{N_x}^k) + \tau^2f(x_{N_x},t_k). \tag{7b}\]

最后需要注意的是, 利用初始条件计算第一个时间层的解时 \((k=1)\), 我们需要同时利用 (5), \(i=0,N_x\) 和 (7a,7b) 确定 \(u_0^{1}\) 和 \(u_{N_x}^{1}\) 满足的方程\[\begin{align} u_0^{1} &=u_0^{0}+\tau \partial_tu(x_0,t_0) + \left( c\frac{\tau}{h} \right)^2 (u_{1}^{0}-u_0^{0}) + \frac{1}{2}\tau^2f(x_0,t_k),\\ u_{N_x}^{1} &=u_{N_x}^{0}+\tau \partial_tu(x_{N_x},t_0) + \left( c\frac{\tau}{h} \right)^2 (u_{N_x-1}^{0}-u_{N_x}^{0}) + \frac{1}{2}\tau^2f(x_{N_x},t_k). \tag{8}\end{align}\]

显式的有限差分 (FD) 算法

综上, 实现有限差分算法大体分为如下几个步骤:

利用 (3) 计算 \(u_i^0\);
利用 (5) 计算 \(u_i^1\), \(i=1,…,N_x-1\); 利用 (8) 计算端点 \(u_0^1, u_{N_x}^1\);
对 \(k=1,…,N_t-1\), 利用 (2) 计算 \(u_i^{k+1}\), \(i=1,…,N_x-1\); 利用 (7a,7b) 计算端点.

数值实验

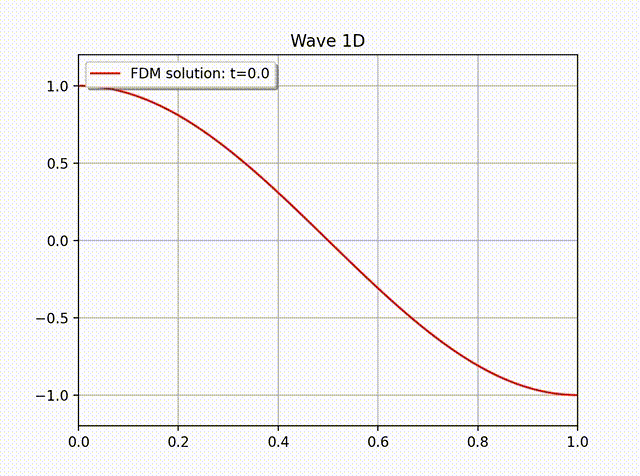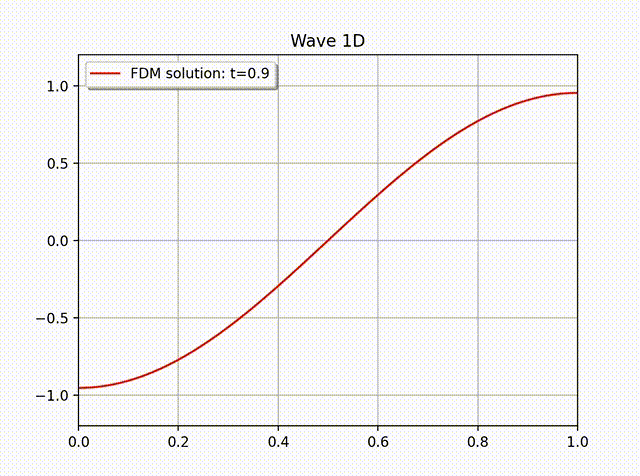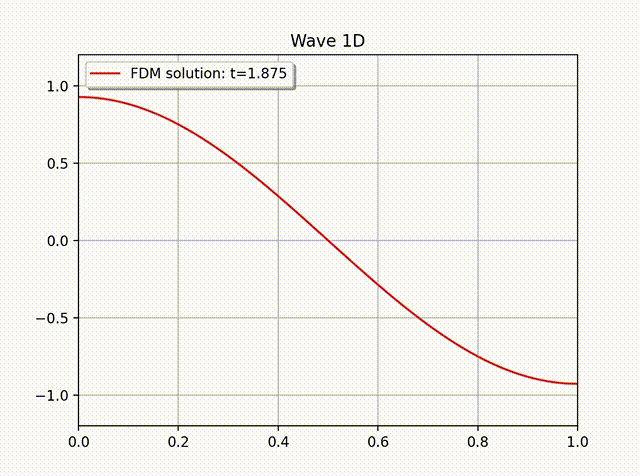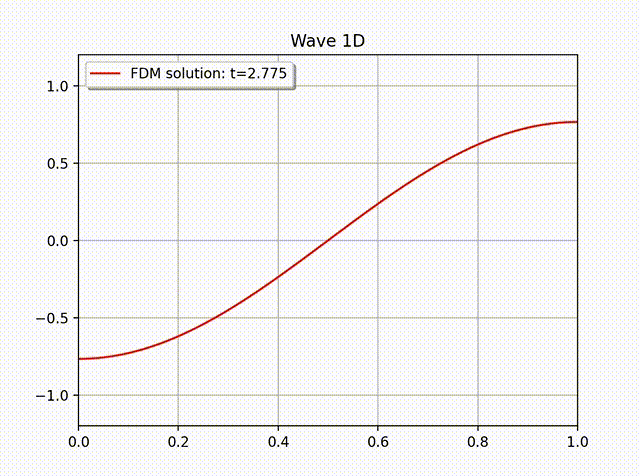
例1 假设方程 (1) 有如下精确解:\[ u(x,t) = A\cos \left( \frac{\pi}{L}x \right) \cos \left( \frac{\pi}{L}ct \right), \quad 0\leq x\leq L.\]其中 \(L=1,A=1,c=1,f=0\), 边界条件为 \(\partial_xu(0,t)=0\), 初始条件为 \(u(x,0)=A\cos \left( \frac{\pi}{L}x \right)\) 和 \(u'(x,0)=0\). 下表中列出的是当 \(N_t=2000\) 时误差随空间步长 \(h\) 变化的情况. 从中可以看出最优收敛速度. 下图是当 \(N_x=20, h=1/N_x; \tau=h/c=1/(cN_x)=64\) 时的数值解图像. 从解的图像中我们大致可以看出数值解是满足齐次 Neumann 边界条件的.

\(N_t=2000\)
\(N_x\)	误差	收敛阶
20	4.8015e-03
40	1.1967e-03	2.00
80	2.9591e-04	2.01
160	7.0734e-05	2.06
320	1.4441e-05	2.29

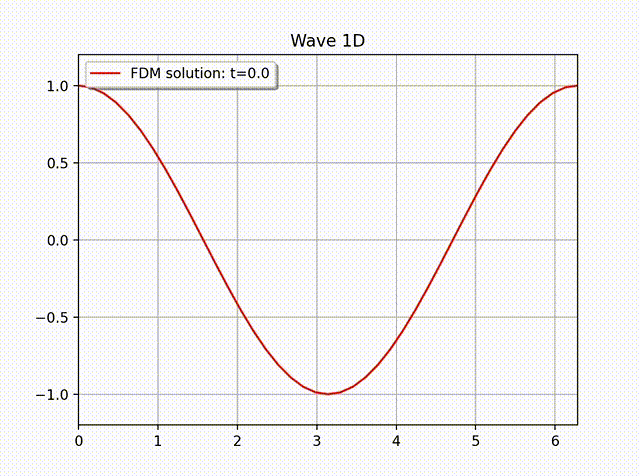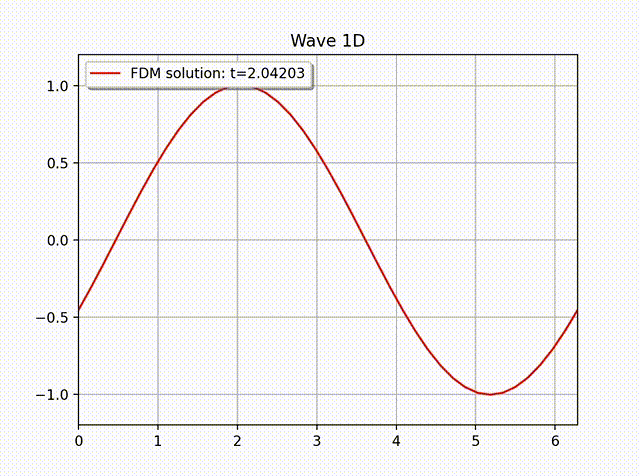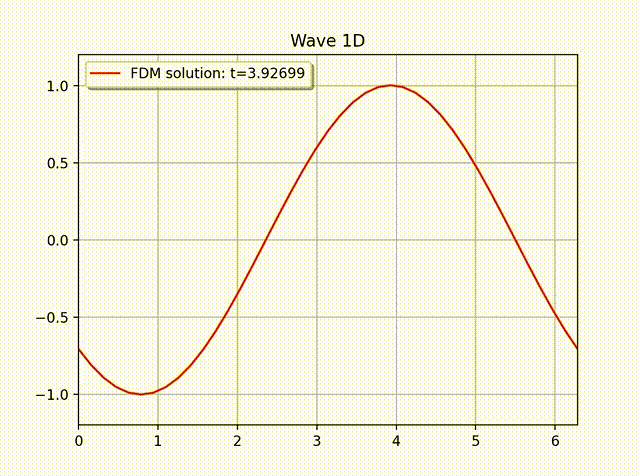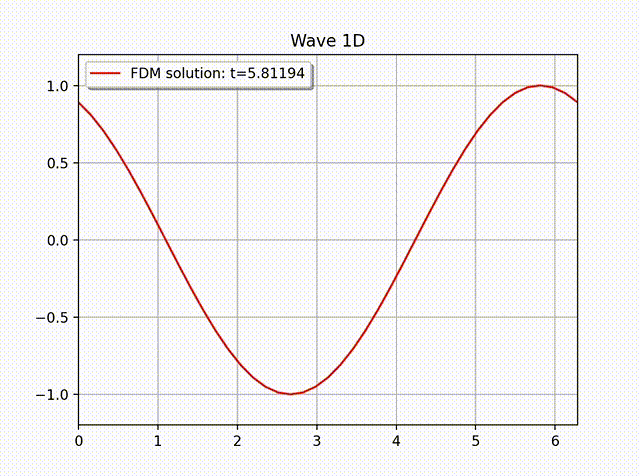
例2 下面我们计算一个具有非齐次边界条件的例子: \[ u(x,t) = \cos \left( x-t \right), \quad 0\leq x\leq 1.\]这是一个右行波函数, 其中 \(L=1,k=1,\omega=1,f=0\), 边界条件为 \(\partial_xu(0,t)=- \sin (x-t)\), 初始条件为 \(u(x,0)=\cos x\) 和 \(u'(x,0)=\sin x\). 从下面的数值解图像中可以看出这个波是向右传动的.