时谐 Maxwell 方程的导出
Maxwell 方程
Maxwell 方程具有如下形式 \[ \begin{equation} \begin{split} \nabla\times \mathcal{E} &= -\frac{\partial \mathcal{B}}{\partial t}, \\ \nabla\times \mathcal{H} &= \frac{\partial \mathcal{D}}{\partial t} + \mathcal{J},\\ \nabla\cdot \mathcal{D} &= \varrho , \\ \nabla\cdot \mathcal{B} &= 0, \end{split} \tag{Eq. 1} \end{equation} \] 其中, \(\mathcal{D}\) 和 \(\mathcal{B}\) 分别表示电位移和磁感应强度, \(\mathcal{E}\) 和 \(\mathcal{H}\) 分别表示电场强度和磁场强度, \(\varrho\) 和 \(\mathcal{J}\) 分别表示电荷密度和电流密度. 方程 (Eq. 1) 可以解释所有的宏观电磁现象, 它是由四个物理学基本定律组成: Faraday 电磁感应定律, Ampere 定律以及电场和磁场的高斯定理. 通过对第二个方程两边进行散度运算并利用第三个方程, 可以得到隐含的连续方程 \[ \frac{\partial \varrho}{\partial t} + \nabla\cdot \mathcal{J}=0. \]
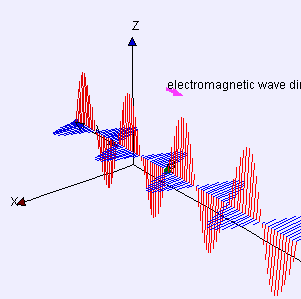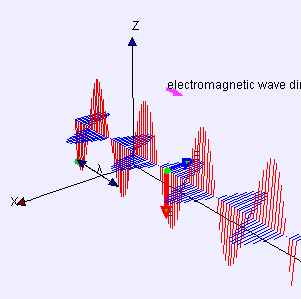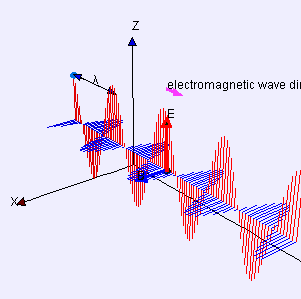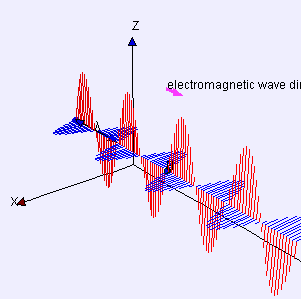
This 3D diagram shows a plane linearly polarized wave propagating from left to right, defined by \(\textbf{E} = \textbf{E}_0 \sin(−\omega t + \textbf{k}\cdot \textbf{r})\) and \(\textbf{B} = \textbf{B}_0 \sin(−\omega t + \bf{k}\cdot \bf{r})\). The oscillating fields are detected at the flashing point. The horizontal wavelength is \(\lambda\). \(\textbf{E}_0 \cdot \textbf{B}_0=0=\textbf{E}_0\cdot \textbf{k}=\textbf{B}_0\cdot \textbf{k}\).
在实际电磁场应用中, 计算区域通常是由几种不同材料构成, 即非齐次各向同性介质, 在这种介质中, 电位移和电场强度以及磁感应强度和磁场强度具有如下的本构关系 \[ \begin{equation} \mathcal{D} = \varepsilon \mathcal{E},\quad \mathcal{B} = \mu \mathcal{H}, \tag{Eq. 2} \end{equation} \] 其中 \(\varepsilon\) 和 \(\mu\) 分别是介质的电介常数和磁导率, 通常假设为分片常数. 在真空中, 它们对应的值分别用常量 \(\varepsilon_0\) 和 \(\mu_0\) 来表示, 并且真空中的光速 \(c=\frac{1}{\sqrt{\varepsilon_0\mu_0}}\). 在真空中, 本构关系 (Eq. 2) 可以简化为 \(\mathcal{D} = \varepsilon_0 \mathcal{E},\ \mathcal{B} = \mu_0 \mathcal{H}\). 另外, 在导电材料中, 电磁场本身是可以产生电流的, 所以我们假定下面的 Ohms 定律成立 \[ \begin{equation} \tag{Eq. 3} \mathcal{J} = \sigma \mathcal{E} + \mathcal{J}_a, \end{equation} \] 其中, \(\sigma\) 表示材料的电导率 (真空中的值为 0), \(\mathcal{J}_a\) 表示施加于磁场中的电流密度.
时谐方程的导出
处于稳态的电磁现象可以由时谐 Maxwell 方程来刻画. 由 Fourier 变换或者令 \[ \begin{align*} \mathcal{E}=\textbf{E} e^{-i\omega t}, \quad \mathcal{D}=\textbf{D} e^{-i\omega t},\\ \mathcal{H}=\textbf{H} e^{-i\omega t}, \quad \mathcal{B}=\textbf{B} e^{-i\omega t}, \end{align*} \] 且定义 \(\mathcal{J}=(\sigma \textbf{E}+\textbf{J}_a) e^{-i\omega t}\) 和 \(\varrho =\rho e^{-i\omega t}\), 由连续性方程可以得到 \(-i\omega \rho + \nabla \cdot (\sigma \textbf{E}+\textbf{J}_a)=0\). 代入方程 (Eq. 1) 中并利用本构关系 (Eq. 2) 和 Ohms 定律 (Eq. 3) 可得 \[ \begin{equation} \begin{split} \nabla\times \textbf{E} &= i\omega \mu\textbf{H}, \\ \nabla\times \textbf{H} &= -i\omega \varepsilon\textbf{E} + \sigma \textbf{E}+\textbf{J}_a,\\ \nabla\cdot \varepsilon\textbf{E} &= \frac{1}{i\omega}\nabla\cdot (\sigma \textbf{E}+\textbf{J}_a), \\ \nabla\cdot \mu\textbf{H} &= 0, \end{split} \tag{Eq. 4} \end{equation} \]
容易验证, 方程 (Eq. 4) 中的前两个等式, 通过利用本构关系 (Eq. 2) 可以消去磁场 \(\textbf{H}\), 得到一个二阶 Maxwell 方程 \[ \begin{equation} \nabla\times \mu^{-1}\nabla\times \textbf{E} -\omega^2 \varepsilon \textbf{E} – i\omega \sigma \textbf{E} = i\omega \textbf{J}_a, \tag{Eq. 5} \end{equation} \]
通过引入相对电介常数 \(\varepsilon_r=\frac{1}{\varepsilon_0} \left( \varepsilon +\frac{i\sigma}{\omega} \right)\) 和相对磁导率 \(\mu_r=\frac{\mu}{\mu_0}\), 并且令波数 \(k=\omega/c\), 那么方程 (Eq. 5) 等价为 \[ \begin{equation*} \begin{split} \nabla\times \mu_r^{-1}\nabla\times \textbf{E} -k^2 \varepsilon_r \textbf{E} &= i\omega \mu_0\textbf{J}_a. %\\ % \nabla\times \varepsilon_r^{-1}\nabla\times \textbf{H} % – k^2 \mu_r \textbf{H}&= \nabla\times \varepsilon_r^{-1} \textbf{J}, \end{split} \end{equation*} \] 这就得到了时谐 Maxwell 方程的基本形式. 在实际应用中, 通常还需要散度条件, 由相对电介常数和磁导率的定义可知, (Eq. 4) 中第三方程等价于 \[ \nabla\cdot \varepsilon_r \textbf{E} = -\frac{i}{\omega \varepsilon_0} \nabla\cdot \textbf{J}_a. \] 至此, 我们就得到了时谐 Maxwell 方程模型问题 \[ \begin{equation} \begin{split} \nabla\times \mu_r^{-1}\nabla\times \textbf{E} -k^2 \varepsilon_r \textbf{E} &= \textbf{f}, \\ \nabla\cdot \varepsilon_r \textbf{E}&= \textbf{h}, \end{split} \tag{Eq. 6} \end{equation} \] 其中, \(\textbf{f} = i\omega \mu_0\textbf{J}\) 且 \(\textbf{h} = -\frac{i}{\omega \varepsilon_0} \nabla\cdot \textbf{J}_a\). 易知, 当电磁场中没有施加外部电流时, 电场的散度为零.
参考
- Assous, F., Ciarlet, P., & Labrunie, S. (2018). Mathematical Foundations of Computational Electromagnetism. Springer.
- Monk, P. (2003). Finite Element Methods for Maxwell’s Equations. In Numerical Mathematics and Scientific Computation.