偏微分方程习题选解: Evans’ PDE Chapter 5 Sobolev Spaces
Abstract. 这是一个习题答案个人总结, 习题来自 Evans 的偏微分方程教材第二版第五章. 仅供参考, 也欢迎提出问题和建议. This is a personal collection of solutions to Evan's PDE book (2ed). Any comment is welcome to improve. 题号 No. [3, 4, 8, 11, 14, 15, 17, 18]
Problems and solutions
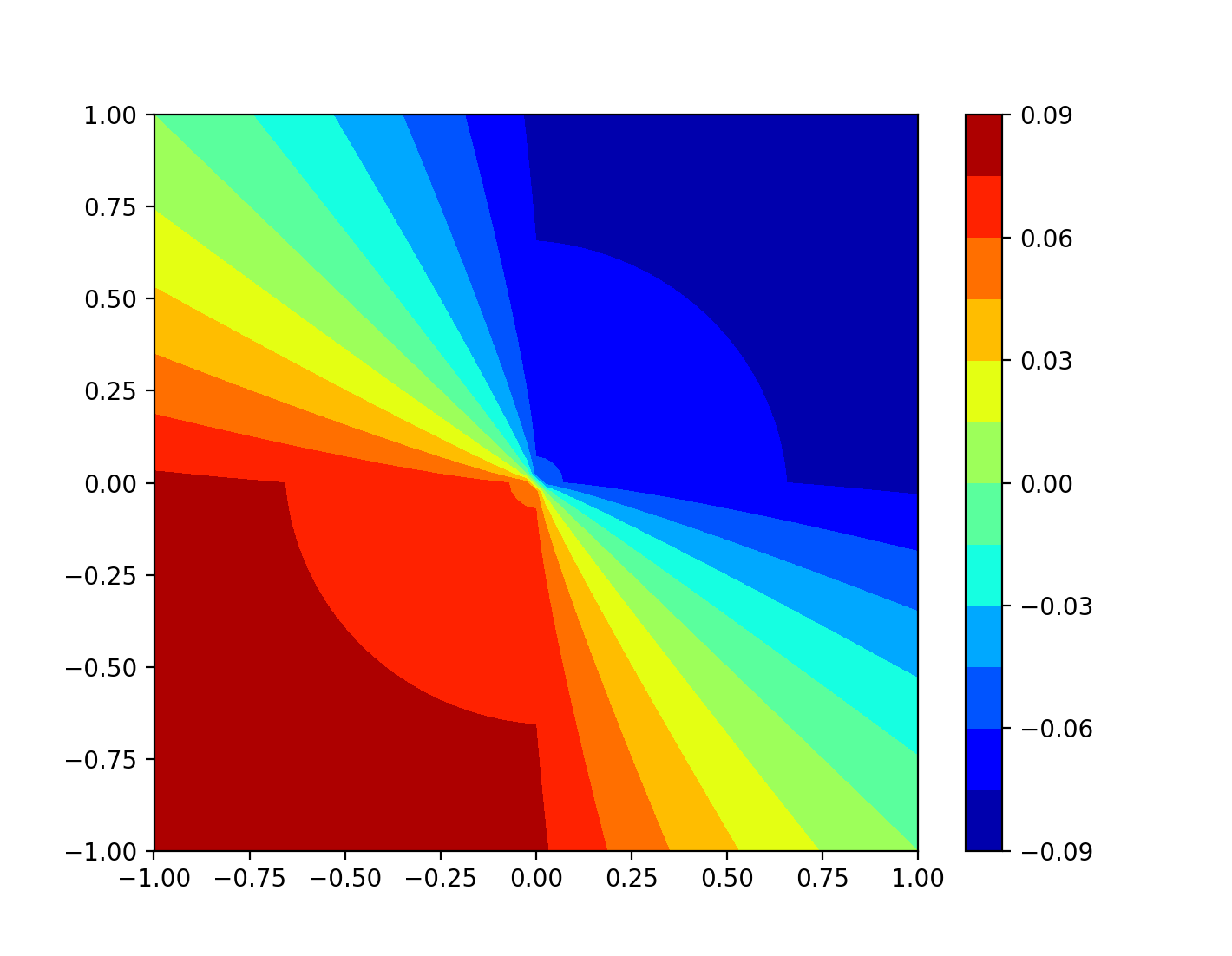
3. Denote by \(U \) the open square \(\{x\in \mathbb{R}^2: |x_1|<1,\ |x_2|<1\}\). Define\[ \begin{equation*} u(x)=\begin{cases} 1-x_1 \quad x_1>0,\ |x_2|< x_1 \\ 1+x_1 \quad x_1 < 0,\ |x_2| < -x_1 \\ 1-x_2 \quad x_2>0,\ |x_1|< x_2 \\ 1+x_2 \quad x_2 < 0,\ |x_1| < -x_2 . \end{cases}\end{equation*}\]For which \(1\leq p\leq \infty\) does \(u\) belong to \(W^{1,p}(U)\)?
Proof. Let \(U_i,i=1,2,3,4\) be the four subdomains. By a direct computation, for any \(\phi\in C_c^\infty(U)\),\[ \int_U u \frac{\partial \phi}{\partial x_1} =\sum_{i=1}^{4} \int_{U_i} u \frac{\partial \phi}{\partial x_1} =\sum_{i=1}^{4} \left( -\int_{U_i} \frac{\partial u}{\partial x_1} \phi dx + \int_{\partial U_i} u\phi \nu_1 ds \right)\]Since \(u \) is continuous over \(U \) and \(\phi=0\) on \(\partial U\), we have\[ \sum_{i=1}^{4}\int_{\partial U_i} u\phi \nu_1 ds =0.\]Hence, from the definition of weak derivative, piecewise derivative, \(\frac{\partial u}{\partial x_1}=-1,1,0,0 \) respectively, on the subdomains, is exactly its weak derivative.
Since \(u,\nabla u\in L^{\infty} \), we know \(u\in W^{1,p} \) for all \(1\leq p\leq \infty \). \(\heartsuit\)
4. Assume \(n=1\) and \(u\in W^{1,p}(0,1)\) for some \(1\leq p<\infty \).
- Show that \(u\) is equal a.e. to an absolutely continuous function and \(u’\) (which exists a.e.) belongs to \(L^p(0,1)\). (Note by the fundamental theorem of Lebesgue integral calculus, we only need to show there exists a Lebesgue integral function \(v(t)\) s.t. \(u(x)=u(a+\int_{a}^x v(t)dt)\).)
- Prove that if \(0<p<\infty \), then\[ |u(x)-u(y)|\leq |x-y|^{1-1/p}\left( \int_0^1 |u’|^p dt\right)^{1/p}\]for a.e. \(x,y \in [0,1]\).
Proof. (Sec 5.3.2, Thm 3) Let \(\phi_j\in C^\infty([0,1]) \) s.t. \(\phi_j\to u \) in \(W^{1,p}(0,1) \), we have\[ \phi_j\to u \quad \text{a.e. }x\in (0,1). \tag{4.1}\]Actually, we can set \(\phi_j \) to be the mollification of \(u \) and apply Appendix C.4 to get (4.1).Hence, for a.e. \(x,y\in (0,1)\)\[ u(y)-u(x) = \lim_{j} [\phi_j(y)-\phi_j(x)] =\lim_{j} \int_x^y \phi_j’ = \int_x^y u’ dt\]and Holder inequality yields\[ |u(y)-u(x)|=\left| \int_x^y u’ dt\right| \leq \left( \int_x^y 1^q dt \right)^{1/q} \left( \int_x^y |u’|^p dt \right)^{1/p},\]where \(\frac{1}{q}=1-\frac{1}{p} \). \(\heartsuit\)
8. Let \(U\) be bounded, with a \(C^1\) boundary. Show that a “typical” function \(u\in L^p(U)(1\leq p<\infty)\) does not have a trace on \(\partial U\). More precisely, prove there does not exist a bounded linear operator\[ T:L^p(U)\to L^p(U)\]such that \(Tu = u_{|\partial U}\) whenever \(u\in C(\bar{U})\cap L^p(U)\).
Proof. If such \(T\) exists, for \(p=2\) example, we have bound\[ \|Tu\|_{L^2(\partial U)}\leq C \|u\|_{L^2(U)} \quad \forall u\in C(\bar{U}).\]Construct a sequence of \(u_n\in C(\bar{U})\) s.t. \[ \|u_n\|_{L^2(U)} \to 0, \quad \text{but}\quad \|u_{|\partial U}\|_{L^2(\partial U)}\to \text{const.}>0.\]Let \(u_n=\frac{1}{1+n \text{dist}(x,\partial U)}\). \(\heartsuit\)
11. Suppose \(U \) is connected and \(u\in W^{1,p}(U) \) satisfies\[ Du=0 \quad \text{a.e. in } U.\]Prove \(u \) is constant a.e. in \(U \).
Proof. Let \(U_\epsilon=\{x\in U:\ \mathrm{dist}(x,\partial \Omega)>\epsilon\}, \epsilon>0 \), by [Sec 5.3.1, Theorem 1, (1)], there holds \[ D u^{\epsilon} = (D u) ^{\epsilon} \quad \text{in }U_{\epsilon}\]Since \(Du=0 \) a.e., we obtain by the assumption\[ D u^{\epsilon} = 0 \quad \text{in }U_{\epsilon}\]that is \(u^\epsilon \) is constant in \(U_\epsilon \). Then, use \(u^\epsilon \to u \) a.e. as \(\epsilon\to 0 \). \(\heartsuit\)
14. Verify that if \(n>1 \), the bounded function \(u=\log \log(1+\frac{1}{|x|}) \) belongs to \(W^{1,n}(U) \), \(U=B^{0}(0,1) \).
Proof. Clearly, for any fixed integer \(n \) there holds \(\lim_{t \rightarrow \infty}\frac{\log(t)^{n}}{t}=0 \). Hence \[ \frac{[\log\log(1+t)]^{n}}{t}=\frac{[\log\log(1+t)]^{n}}{[\log(1+t)]^{n}} \frac{[\log(1+t)]^{n}}{t} \rightarrow 0, \text{ as } t \rightarrow 0.\]We claim \(u\in L^{n}(U) \). In fact,\[ \begin{align*} \|u\|_{L^{n}(U)}^{n} &=\int_{U}[\log\log(1+\frac{1}{|x|})]^{n}dx \\ &=\int_{0}^{1}[\log\log(1+\frac{1}{r})]^{n}n \alpha(n)r^{n-1}dr \\ &=n \alpha(n)\int_{1}^{\infty}\frac{[\log\log(1+t)]^{n}}{r}\frac{1}{r^{n}}dt <\infty.\end{align*}\]We know from fundamental calculus \[\frac{\partial u}{\partial x_{i}}=\frac{1}{\log(1+1/|x|)}\frac{1}{1+1/|x|}\frac{-x_{i}}{|x|^{3}},\]and\[\begin{align*}\left\|\frac{\partial u}{\partial x_{i}}\right\|_{L^{n}(U)}^{n} & \leq n \alpha(n)\int_{0}^{1} \frac{1}{\log(1+1/r)}\frac{1}{1+1/r} \frac{1}{r^{2}} r^{n-1} dr\\& = n \alpha(n)\int_{1}^{\infty} \frac{1}{\log(1+t)}\frac{t}{1+t} \frac{1}{t^{n}} dt <\infty.\\\end{align*}\]Hence \(u\in W^{1,n}(U) \). \(\heartsuit\)
15. Fix \(\alpha>0 \) and let \(U=B_1^0(U) \). Show that there exists a constant \(C>0 \), depending only on \(n \) and \(\alpha \), such that \[ \int_{U}u^2 dx \leq C \int_{U}|Du|^2 dx,\]provided\[ |\{x\in U\ |\ u(x)=0\}|\geq \alpha , \quad u\in H^1(U).\]
Proof. Let \((u)_{U} \) be the average of \(u \) over \(U \). By using Poincare inequality [Sec 5.8, Thm 1], we have\[ \begin{align*} \|u\|_{L^{2}(U)}\leq \|u-(u)_{U}\|_{L^{2}(U)}+\|(u)_{U}\|_{L^{2}(U)} \leq C(n,U) \|Du\|_{L^{2}(U)}+\|(u)_{U}\|_{L^{2}(U)}. \end{align*}\]Since\[ \begin{align*} \|(u)_{U}\|_{L^{2}(U)} &\leq \frac{1}{|U|^{1/2}}\int_{U\setminus \{ u=0 \}}|u| \\ &\leq \frac{1}{|U|^{1/2}} \|1\|_{L^{2}(U\setminus \{ u=0 \})}\|u\|_{L^{2}(U\setminus \{ u=0 \})} \\ &\leq \frac{(|U|-\alpha)^{1/2}}{|U|^{1/2}}\|u\|_{L^{2}(U)},\end{align*}\]substituting into the above inequality, it holds true\[ \begin{equation*} \left( 1- \frac{(|U|-\alpha)^{1/2}}{|U|^{1/2}}\right)\|u\|_{L^{2}(U)} \leq C(n,U) \|Du\|_{L^{2}(U)}.\end{equation*}\]\(\heartsuit\)
17. Let \(U \in \mathbb{R}^n\) be a bounded domain, \(1\leq p\leq \infty \) and \(f\in C^1(\mathbb{R})\) with \(f’\in L^{\infty}(\mathbb{R}^n)\). Prove that \(v=f\circ u\in W^{1,p}(U)\) whenever \(u\in W^{1,p}(U)\), and that \[ v_{x_i}=f'(u)u_{x_i},\quad 1\leq i\leq n.\]
Proof. Take smooth sequence \(u_m\in C^{\infty}(U) \) such that \(u_m\to u \) in \(W^{1,p}(U) \) as \(m\to \infty \), for example we can take \(u_m \) to be the mollification of \(u \), and hence we know \[ \tag{17.1} u_m \to u,\ D_{x_i}u_{m}\to D_{x_i}u \quad \text{a.e. on } U.\]To show \(f(u)\in W^{1,p}(U) \), we need to show \(f(u)\in L^p(U) \) and its weak derivatives are in \(L^p(U) \). Let \(x_0\in U \) be a Lebesgue point of \(u \). Because \(f\in C^1(\mathbb{R}) \) and \(f’\in L^{\infty}(\mathbb{R}) \), we have for a.e. \(x\in U\)\[ f(u(x)) = f(u(x_0)) + \int_{0}^{u(x)} f'(t) dt \leq |f(u(x_0))| + \|f’\|_{L^\infty(U)} |u(x)|\]Because \(|f(u(x_0))| \) and \(\|f’\|_{L^\infty(U)} \) are constant, we deduce \(f(u)\in L^p(U) \) by the boundedness of \(U \) and \(u\in L^p(U) \).
Secondly, since \(f'(u)\in L^\infty(U) \) and \(D_{x_i}u\in L^p(U) \), we have \(f'(u)D_{x_i}u\in L^p(U) \). For any \(\phi\in C^\infty_0(U) \), there holds \[ \begin{align*} \int_{U}f(u)\phi’ &= \int_{U}f(u_m)D_{x_i}\phi + \int_{U}[f(u_m)-f(u)]D_{x_i}\phi \\ &= – \int_{U}[f'(u_m) D_{x_i}u_m]\phi + \int_{U}[f(u_m)-f(u)]D_{x_i}\phi \\ &\to – \int_{U}[f'(u) D_{x_i}u]\phi, \end{align*}\]where we have used (17.1) and dominated convergence and the following limit as \(m \) tends to infinity\[ \int_{U}[f(u_m)-f(u)]D_{x_i}\phi \leq \|f(u_m)-f(u)\|_{L^p(U)} \|D_{x_i}\phi\|_{L^q(U)} \leq C \|f’\|_{L^\infty(\mathbb{R})} \|u_m-u\|_{L^p(U)} \to 0\]\(\heartsuit\)
18. Assume \(1\leq p\leq \infty \) and \(U\) a bounded domain.
1. Prove that if \(u\in W^{1,p}(U)\), then \(|u|\in W^{1,p}(U)\).
2. Prove \(u\in W^{1,p}(U)\) implies \(u^+=\max \left\{ u,0 \right\}\) and \(u^-=-\min \left\{ u,0 \right\}\) in \(W^{1,p}(U)\) with \[ Du^{\pm}=\begin{cases} \pm Du & \text{a.e. on } \left\{ \pm u>0 \right\},\\ \pm 0 & \text{a.e. on } \left\{ \pm u\leq 0 \right\}. \end{cases}\](Hint). \(u^+=\lim_{\epsilon \to 0} F_\epsilon(u)\) for \[ F_\epsilon(z)=\begin{cases} (z^2+\epsilon^2)^{1/2}-\epsilon & \text{if } z\geq 0,\\ 0 & \text{if } z< 0. \end{cases}\]
3. Prove that if \(u\in W^{1,p}(U)\), then\[ Du=0\quad \text{a.e. on } \left\{ u=0 \right\}.\]
Proof. First, prove 2). It is easy to show for any fixed \(\epsilon>0 \), \(F_\epsilon \in C^1(\mathbb{R}) \) and \(F_\epsilon’ \in L^{\infty}(\mathbb{R}) \). In fact,\[ F_\epsilon'(z) = \frac{z}{\sqrt{z^2+\epsilon^2}}, z> 0;\ \text{ and } F_\epsilon'(z) = 0,\ z\leq0.\]By using the definition of weak derivative and problem 2, it holds for \(\phi\in [C^\infty_0(U)]^d\)\[ \int_{U}F_\epsilon(u) D\phi = -\int_{U}[F_\epsilon(u)’Du] \phi = -\int_{\{u\geq 0\}}Du \frac{u}{\sqrt{u^2+\epsilon^2}} \phi\]Since \(|Du \frac{u}{\sqrt{u^2+\epsilon^2}}|\leq |Du| \) and \(|Du| \) is integrable, the dominated convergence theorem applies to the right-hand side of the latter identity. Similarly, since \(F_\epsilon(u)\to u^+ \) a.e. as \(\epsilon\to 0 \) and \(|F_\epsilon(u)|\leq |u| \), the dominated convergence theorem also applies the the left-hand side. By taking \(\epsilon\to 0 \) we thus have\[ \int_{U}u^+ D\phi = – \int_{\{u> 0\}}Du \phi,\]which says \(Du^+=\begin{cases} Du, \quad & \text{on }\{u> 0\} \\ 0,& \text{on }\{u\leq 0\}\end{cases}\). The case of \(u^- \) is similar.
1) Since \(|u|=u^+ + u^- \) and from b) we know \(u^{\pm}\in W^{1,p}(U) \), thus, also \(|u|\in W^{1,p}(U) \).
3) We already know \(Du^{\pm}=0 \) a.e. on \(\{\pm u\leq 0\} \), hence \(Du = Du^+ + Du^-=0 \) a.e. on \(\{u=0\}=\{u\leq 0\}\cap\{u\geq 0\} \). \(\heartsuit\)
References
[1] Evans, L. C. (2010). Partial differential equations. In Graduate studies in mathematics (2nd ed.). American Mathematical Society.