一个复变函数的极小值

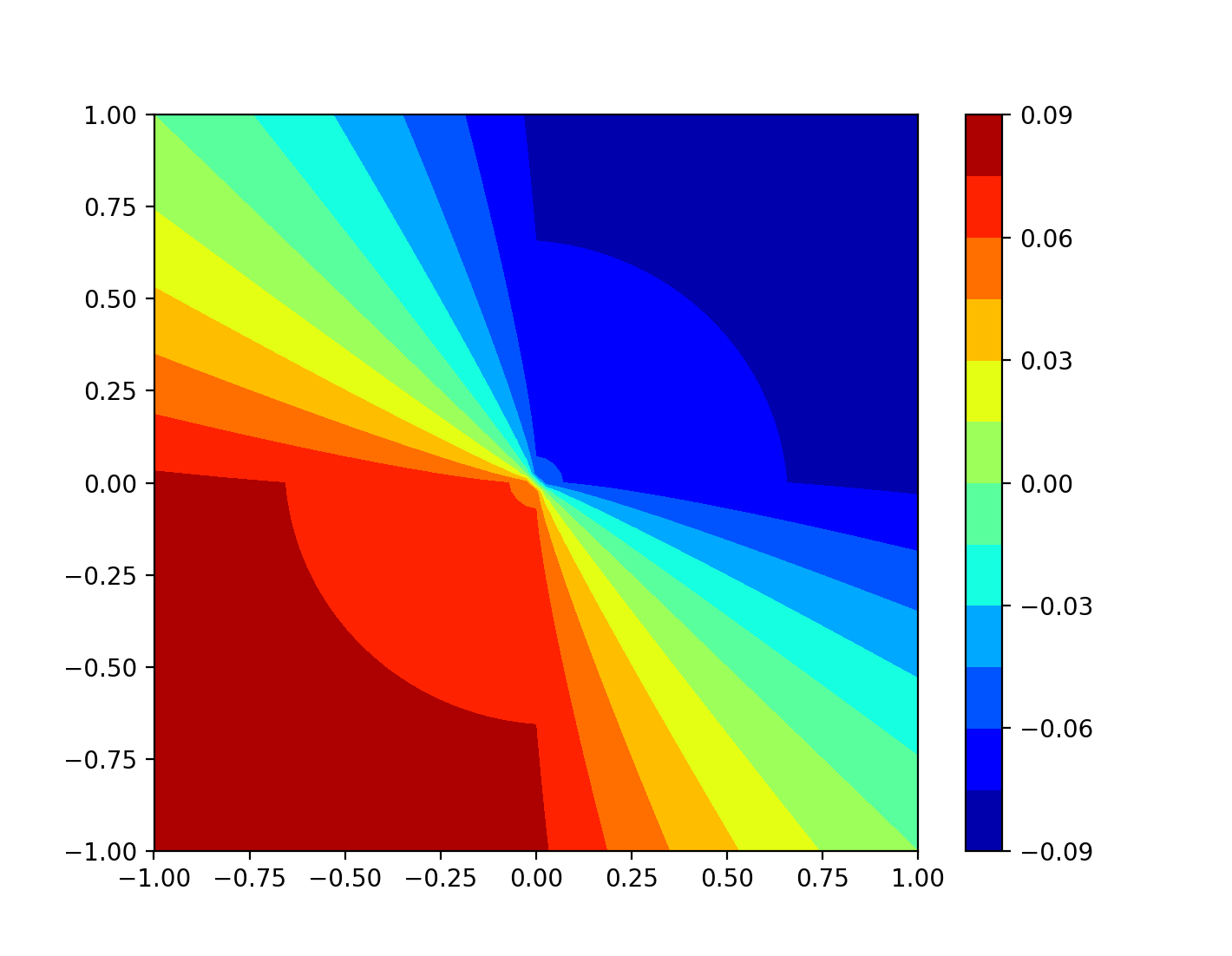
问题. 证明存在一个正数 \(\gamma>0\) 使得\[ \min_{s \in \mathcal{U}} |f(s)|\geq \gamma>0,\]其中 \(\mathcal{U}=\left\{ s \in \mathbb{C}:\ \Re (s)>0, |s|\leq 1 \right\}\), 复变函数定义如下\[ f(s)=s+\sqrt{s^2+1-|s|^2}.\]

证明. 由 \(1-|s|\geq 0\) 可知\[ -\pi/2 <= \arg(s) <= \pi/2,\\ -\pi <= \arg(s^2) <= \pi,\\ -\pi <= \arg(s^2+1-|s|^2) <= \pi,\\ -\pi/2 <= \arg(\sqrt{s^2+1-|s|^2}) <= \pi/2.\]

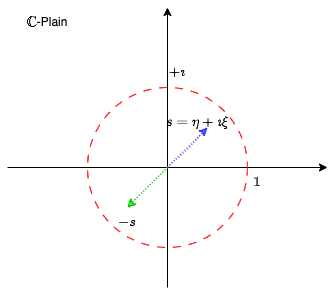
• 情形 1. \(\Im (s)\neq 0\). \(f(s)=0\) 表明\[ -s = \sqrt{s^2+1-|s|^2}.\]上面的等式不可能成立. 事实上, 当 \(\Im (s)>0\) 时, \(\Im (-s)<0\). 然而, \(\Im (\sqrt{s^2+1-|s|^2})>0\). 矛盾.
• 情形 2. \(\Im (s)=0\). 在此情况下 \(f(s)=\Re (s)+1\geq 1\).

综上可知, 函数 \(f(s)\) 在区域 \(\bar{\mathcal{U}}\) 上不可能存在零点, 又因为函数的连续性, 所以存在正数 \(\gamma>0\) 使得 \(|f(s)|\geq \gamma>0\). \(\heartsuit\)