几类常用的插值方法简介

插值

我们知道, \(n+1\) 个实数可以唯一确定一个 \(n\) 次多项式\[ p_n(x)=a_nx^n+a_{n-1}x^{n-1}+\dots+a_1x+a_0.\]在数值分析中, 多项式在函数逼近领域非常重要并且使用非常频繁, 原因有多种:

• 代数多项式本身及其导数构造简单.
• 具有一致逼近性质 (Weierstrass 定理).

定理 (Weierstrass). 假设函数 \(f\in C([a,b])\), 那么对任意正数 \(\epsilon>0\) 都存在一个多项式 \(p(x)\) 使下式成立\[ \max_{a\leq x\leq b} |f(x)-p(x)|< \epsilon. \tag{1}\]

给定 \(n+1\) 个离散的插值点数据\[ (x_0,y_0), (x_1,y_1), \ldots, (x_n,y_n).\]

Lagrange 插值

\[ P_n(x)=\sum_{k=0}^n y_k L_k(x), \quad L_k(x) = \prod_{i=0,i\neq k}^{n}\frac{x-x_i}{x_k-x_i}.\]这样得到多项式的显示表达式并且精确满足插值点数据: \(y_j=P_n(x_j)\).

定理 1 (余项估计). 令 \(f(x)\in C^n[a,b]\) 并假设 \(f^{(n+1)}(x)\) 在区间 \((a,b)\) 上是有定义的.\[ R_n(x):=f(x)-p_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}\prod_{i=0}^n (x-x_i) \tag{2}\]其中, \(a<\xi(x)< b \) 与 \(x\) 相关.

证明. 首先, 明显可以看出 \(R_n(x_i)=f(x_i)-p_n(x_i)=0\), 满足等式 (2). 现假设任意给定 \(x\neq x_i\), 并定义如下函数:\[ g(t)=f(t)-p_n(t) – \left[ f(x)-p_n(x) \right] \prod_{i=0}^n \frac{t-x_i}{x-x_i},\quad t\in [a,b].\]容易验证 \(g(x)=g(x_i)=0, i=0,1,\ldots ,n\), 即存在 \(n+2\) 个不同的零点; 从而由广义的 Rolle 中值定理可知, 存在一个实数 \(\xi\in (a,b)\) 使得 \(g^{(n+1)}(\xi)=0\). 通过计算可知\[ 0=g^{(n+1)}(\xi) = f^{(n+1)}(\xi) – \left[ f(x)-p_n(x) \right] (n+1)! \prod_{i=0}^n \frac{1}{x-x_i}.\]化简后即可得到 (2). \(\heartsuit\)

误差公式 (2) 是一个非常重要的理论结果, 因为 Lagrange 插值广泛应用于数值微分和数值积分方法的推导中, 并且在相应的误差估计中发挥重要作用. 值得注意的是, (2) 与函数在某点处的 Taylor 级数展开非常相似, 不同的地方在于这里的误差是依赖于不同的插值点的. 另外, 先验误差估计 (2) 说明了对任一个光滑函数 (至少 \(n+1\) 阶导数存在), 它与插值多项式之间的误差随多项式阶数的增加而减小. 但是, Runge 现象告诉我们, 单纯地通过增加多项式的次数并不一定能达到一致收敛的目的, 尤其是当函数的解析域过小的时候. 最后, 我们想对 Runge 现象再多做一些解释, 它并不与 Weierstrass 定理相矛盾, 因为一个特殊的插值多项式不收敛并不能说明其它插值不收敛. 事实上, 如果在 Runge 现象的例子中通过 Chebyshev 节点 (原来的是等距节点) 做插值的话, 相应的插值多项式是可以达到一致收敛的.

例 1. 考虑 \(X=\left\{ 0, 0.2, 0.4, 0.6, 0.8, 1.0 \right\}\) 等 \(6\) 个不同的点, 构造 Lagrange 基函数 \(L_2(x)\). 由定义可知\[ L_2(x) = \prod_{i=0,\ i\neq 2}^{n}\frac{x-x_i}{x_k-x_i}=\begin{cases} 1 & x=x_2, \\ 0 & x= x_j,\ j \neq 2. \end{cases}\]

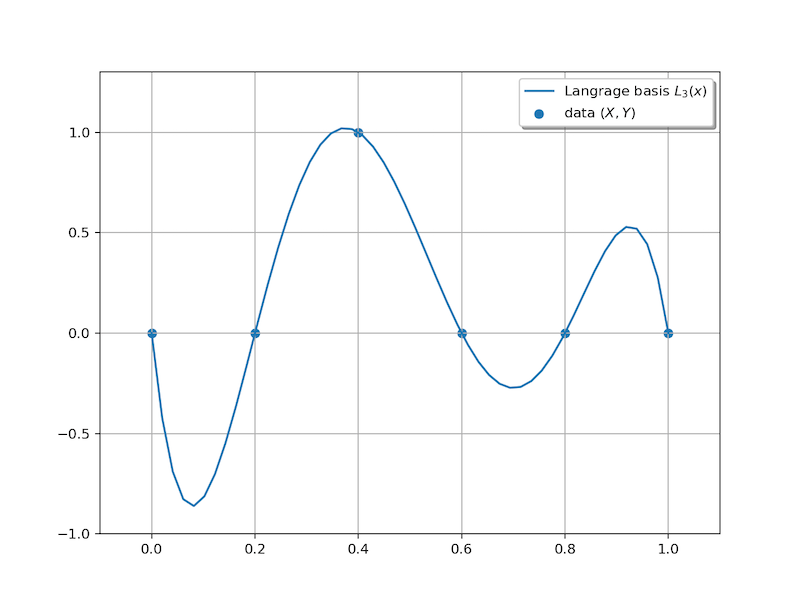
Neville 方法

这种方法不需要显示地求出插值多项式的表达式, 并且可以通过任意增加新的数据来增加插值结果的精度. 例如, 给定点 \(x\), 我们想要计算相应的插值多项式的值 \(y\).\[ \begin{array}{|cc|ccc|} x & y & \\ x_0 & y_0 & \\ x_1 & y_1 & Q_{1,1} = \frac{(x-x_0)y_1 – (x-x_1)y_0}{x_1-x_0} & \\ x_2 & y_2 & Q_{2,1} = \frac{(x-x_1)y_2 – (x-x_2)y_1}{x_2-x_1} & Q_{2,2} = \frac{(x-x_0)Q_{2,1} – (x-x_2)Q_{1,1}}{x_2-x_0}\\ x_3 & y_3 & Q_{3,1} = \frac{(x-x_2)y_3 – (x-x_3)y_2}{x_3-x_2} & Q_{3,2} = \frac{(x-x_1)Q_{3,1} – (x-x_3)Q_{2,1}}{x_3-x_1} & Q_{3,3} = \frac{(x-x_0)Q_{3,2} – (x-x_3)Q_{2,2}}{x_3-x_0} \end{array}\]其中, \(Q_{3,3}\) 就是我们需要计算的 \(y\). 如果这个精度并不能达到所需的精度, 我们可以再增加一行数据 \((x_4,y_4)\), 并计算对应的 \(Q_{4,i}, i=1,2,3,4\). 最后得到的 \(Q_{4,4}\) 就是新的 \(y\).

Neville 方法的一个理论基础如下.

定理 2. 令 \(x_i,x_j\in X:=\left\{ x_k,k=0,1,\ldots,n \right\}\) 是两个不同的插值点, 且 \(P_{-i}(x)\) 为集合 \(X\) 上除 \(x_i\) 之外的 \(n-1\) 次插值多项式. 那么 \(X\) 上的 \(n\) 次 Lagrange 插值多项式可以表示为\[ p_{n}(x) = \frac{(x-x_j)P_{-j}(x)-(x-x_i)P_{-i}(x)}{x_i-x_j}. \tag{3}\]证明. 我们要证明 \(p_{n}(x_k)=y_k,k=0,1,\ldots ,n\). 利用 \(P_{-j}(x_i)=y_i\) 可知\[ p_{n}(x_i) = \frac{(x_i-x_j)P_{-j}(x_i)-(x_i-x_i)P_{-i}(x_i)}{x_i-x_j} =y_i.\]类似地, 可以推出 \(p_{n}(x_j)=y_j\). 最后, 对任意 \(x_k,k\neq i, k\neq j\),\[ p_{n}(x_k) = \frac{(x_k-x_j)y_k-(x_k-x_i)y_k}{x_i-x_j}=y_k.\]

Newton 插值

令 \(x_0,x_1,…,x_n\) 为 \(n+1\) 个不重合的点, 那么就有如下线性无关的 Newton 多项式\[ 1, x-x_0, (x-x_0)(x-x_1),…, (x-x_0)(x-x_1)\cdots(x-x_{n-1}).\]给定函数值 \(f(x_i),i=0,1,…,n\) 存在唯一的多项式满足 \(p_n(x_i)=f(x_i)\):\[ p_n(x) = a_0+a_1(x-x_0)+\ldots +a_n (x-x_0)(x-x_1)\cdots(x-x_{n-1}). \tag{4}\]如果分别令 \(x=x_0, …, x_n\), 我们可以求得系数 \(a_i\)\[\begin{align*} a_0 & = f[x_0] = f(x_0) \\ a_1 & = f[x_0, x_1] = \frac{f(x_1)-f(x_0)}{x_1-x_0} \\ a_2 & = f[x_0, x_1,x_2]= \frac{1}{x_2-x_0}\left( \frac{f(x_2)-f(x_1)}{x_2-x_1} – \frac{f(x_1)-f(x_0)}{x_1-x_0} \right) \\ \cdots \\ a_n & = f[x_0, x_1, \cdots, x_k ] \\\end{align*}\]其中的差商定义如下\[ f[x_0, x_1,\cdots, x_k ] = \frac{f[x_1,\cdots, x_k]-f[x_0,\cdots, x_{k-1}]}{x_k-x_0}. \tag{5a}\]利用归纳法可以证明下面的差商的另一种形式\[ f[x_0, x_1,\cdots, x_n ] = \sum_{k=0}^n \frac{f(x_k)}{(x_k-x_0)\cdots(x_k-x_{k-1})(x_k-x_{k+1})\cdots (x_k-x_{n})}. \tag{5b}\]\[ \begin{array}{|cc|ccc|} x & y & \\ x_0 & y_0 & \\ x_1 & y_1 & f[x_0,x_1] = \frac{f[x_1]-f[x_0]}{x_1-x_0} & \\ x_2 & y_2 & f[x_1,x_2] = \frac{f[x_2]-f[x_1]}{x_2-x_1} & f[x_0,x_1,x_2] = \frac{f[x_1,x_2]-f[x_0,x_1]}{x_2-x_0}\\ x_3 & y_3 & f[x_2,x_3] = \frac{f[x_3]-f[x_2]}{x_3-x_2} & f[x_1,x_2,x_3] = \frac{f[x_2,x_3]-f[x_1,x_2]}{x_3-x_1} & f[x_0,x_1,x_2,x_3] = \frac{f[x_1,x_2,x_3]-f[x_0,x_1,x_2]}{x_3-x_0} \end{array}\]

如果我们增加一个插值点 \((x, f(x))\), 利用相同的方法, 新的插值多项式满足\[ f(x) = p_{n+1}(x) = p_n(x) + f[x, x_0, x_1,\cdots, x_n ] (x-x_0)(x-x_1)\cdots(x-x_{n}),\]等价地, 下面的误差方程成立\[ f(x)-p_n(x) = f[x, x_0, x_1,\cdots, x_n ] (x-x_0)(x-x_1)\cdots(x-x_{n}),\quad \forall x\in [a,b]. \tag{6a}\]如果假设函数 \(f\) 足够光滑, 我们可以得到一个更加具体的逼近结果. 首先, 不难证明如下结论.

定理 3. 令 \(f\in C^{n}[a,b]\), \(x_0,x_1,\dots,x_n\) 是相互不同的点, 那么存在一个常数 \(\xi\in (a,b)\) 满足如下等式\[ f[x, x_0, x_1,\cdots, x_n ] = \frac{f^{(n)}(\xi)}{n!}.\]
证明过程主要利用函数 \(g(x):=f(x)-p_{n}(x)\) 存在 \(n+1\) 个零点, 不再赘述. 通过利用上面的引理, 误差方程 (6) 可以写成如下我们更加熟悉的形式:\[ f(x)-p_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!} (x-x_0)(x-x_1)\cdots(x-x_{n}),\quad \forall x\in [a,b], \tag{6b}\]其中, \(a<\xi< b \) 依赖于 \(x\). 显然, (6b) 就是定理 1中的误差公式.

前向插值

当数据点满足 \(x_i=x_0+ih\) 且 \(x=x_0+sh\) 时, Newton 插值满足\[\begin{align*} p_n(x) &= f[x_0]+f[x_0,x_1](x-x_0)+\ldots +f[x_0,\ldots ,x_n](x-x_0)(x-x_1)\cdots(x-x_{n-1})\\ &= f[x_0]+ \sum_{k=1}^n h^k s(s-1)\ldots (s-k+1) f[x_0,\ldots ,x_k]\\ &= f[x_0]+ \sum_{k=1}^n \begin{pmatrix} s\\ k \end{pmatrix}k!h^k f[x_0,\ldots ,x_k],\end{align*} \tag{7a}\]其中, \(\begin{pmatrix} s\\ k \end{pmatrix} = \frac{s(s-1)\ldots (s-k+1)}{k!}\).
通过引入前向差分算子 \(\Delta\) 并利用 \(x_j-x_i=(j-i)h\), 可以得到\[\begin{align*} f[x_0,x_1] &= \frac{f(x_1)-f(x_0)}{x_1-x_0} = \frac{\Delta f(x_0)}{h},\\ f[x_0,x_1,x_2] &= \frac{1}{2h}\frac{\Delta f(x_1)-\Delta f(x_0)}{h}=\frac{1}{2h^2}\Delta^2 f(x_0),\\ &\ldots \\ f[x_0,x_1,\ldots,x_k] &= \frac{1}{k!h^k}\Delta^k f(x_0).\end{align*}\]将其代入牛顿插值公式可得\[ p_n(x)=f[x_0]+ \sum_{k=1}^n \begin{pmatrix} s\\ k \end{pmatrix} \Delta^k f(x_0). \tag{7b}\]

后向插值

当插值点是逆向排列的时候, \(x_n, x_{n-1},\ldots,x_0\), 定义 \(x:=x_n+sh\), 那么 \(x_i=x_n+(i-n)h\) 并且相应的插值多项式为\[\begin{align*} p_n(x) &= f[x_n]+f[x_n,x_{n-1}](x-x_n)+\ldots +f[x_n,\ldots ,x_0](x-x_n)(x-x_{n-1})\cdots(x-x_1)\\ &= f[x_n]+ \sum_{k=1}^n h^k s(s+1)\ldots (s+k-1) f[x_0,\ldots ,x_n]\\ &= f[x_n]+ \sum_{k=1}^n (-1)^k\begin{pmatrix} -s\\ k \end{pmatrix}k!h^k f[x_0,\ldots ,x_n],\end{align*} \tag{8a}\]

定义 1. 后向差分算子 \(\nabla \) 如下: 对于序列 \(\left\{ y_n \right\}_{n=0}^\infty\),\[ \nabla y_n = y_n-y_{n-1},\quad n\geq 1,\]高阶差分算子定义如下:\[ \nabla ^k y_n = \nabla (\nabla ^{k-1}p_n),\quad k\geq 2.\]从而\[\begin{align*} f[x_n,x_{n-1}] &= \frac{f(x_{n-1})-f(x_{n})}{x_{n-1}-x_{n}} = \frac{\nabla f(x_n)}{h},\\ f[x_n,x_{n-1},x_{n-2}] &= \frac{1}{-2h}\frac{\nabla f(x_{n-1})-\nabla f(x_n)}{h}=\frac{1}{2h^2}\nabla^2 f(x_n),\\ &\ldots \\ f[x_0,x_1,\ldots,x_k] &= \frac{1}{k!h^k}\nabla^k f(x_n).\end{align*}\]将其代入牛顿插值公式 (9) 可得\[ p_n(x)=f[x_0]+ \sum_{k=1}^n (-1)^k\begin{pmatrix} -s\\ k \end{pmatrix} \nabla^k f(x_n). \tag{8b}\]

Hermite 插值

定义. 考虑区间 \([a,b]\) 上 \(n+1\) 个不同的点 \(x_0,x_1,\ldots,x_n\). 令 \(f\in C^1[a,b]\). Hermite 逼近多项式是满足如下条件的最低阶的多项式 \(p(x)\)\[ H(x_i)=f(x_i),\quad H^\prime(x_i)=f^\prime(x_i),\quad i=0,1,\ldots,n.\]

下面, 我们考虑利用 Newton 插值方法来构造 Hermite 多项式.\[ H_{2n+1}(x)=f[z_0]+\sum_{k=1}^{2n+1} f[z_0,…,z_k](x-z_0)(x-z_1)\ldots(x-z_{k-1}),\]其中, (相同点处的一阶差分由导数来代替, 其它与 Newton 插值完全相同)\[ \begin{array}{|cc|c|c|} z & f(z) & & \\ z_0=x_0 & f[z_0]=f(x_0) & \\ z_1=x_0 & f[z_1]=f(x_0) & f[z_0,z_1] = f^\prime(x_0) & \\ z_2=x_1 & f[z_2]=f(x_1) & f[z_1,z_2] = \frac{f[z_2]-f[z_1]}{z_2-z_1} & f[z_0,z_1,z_2] = \frac{f[z_1,z_2]-f[z_0,z_1]}{z_2-z_0}\\ z_3=x_1 & f[z_3]=f(x_1) & f[x_2,x_3] = f^\prime(x_1) & f[z_1,z_2,z_3] = \frac{f[z_2,z_3]-f[z_1,z_2]}{z_3-z_1} \\ z_4 = x_2 & f[z_4]=f(x_2) & f[z_3,z_4] = \frac{f[z_4]-f[z_3]}{z_4-z_3} & f[z_2,z_3,z_4] = \frac{f[z_3,z_4]-f[z_2,z_3]}{z_4-z_2}\\ z_5 = x_2 & f[z_5]=f(x_2) & f[x_2,x_3] = f^\prime(x_2) & f[z_3,z_4,z_5] = \frac{f[z_4,z_5]-f[z_3,z_4]}{z_5-z_3} \end{array}\]

三次样条插值

定义. 给定区间 \([a,b]\) 上的连续函数 \(f\) 和节点 \(a=x_0< x_1 <\ldots < x_n=b\), 那么三次样条插值 \(S(x)\) 多项式满足如下条件:

1. \(S(x)\) 在每一个区间 \([x_j,x_{j+1}],j=0,\ldots ,n-1\) 上是一个三次多项式, 记作 \(S_j(x)\);
2. \(S_j(x_j)=f(x_j)\) 且 \(S_j(x_{j+1})=f(x_{j+1}), j=0,\ldots ,n-1\); 可以看出在内部节点处满足\[ S_j(x_{j+1}) =S_{j+1}(x_{j+1});\]
3. 在内部节点处还满足 (\(j=0,1,\ldots,n-2\)):\[\begin{align*} S_j^\prime(x_{j+1}) &=S_{j+1}^\prime(x_{j+1}),\\ S_j^{\prime\prime}(x_{j+1}) &=S_{j+1}^{\prime\prime}(x_{j+1});\\\end{align*}\]
4. 边界节点满足如下条件之一: (i) \(S^{\prime\prime}(x_0) =S^{\prime\prime}(x_{n})=0\); (ii) \(S^{\prime}(x_0)=f^\prime(x_0)\) 且 \( S^{\prime}(x_n)=f^{\prime}(x_{n})=0\);

因为 \(S(x)\) 是分片三次多项式, 所以总共有 \(4n\) 个未知数, 因此我们必须有相同数量的方程才可以唯一确定 \(S(x)\). 由定义可知, 前三个条件包括的方程个数为\[ 2n (连续性) + 2(n-1) (可微性) + 2(边界条件)=4n.\tag{9}\]

自然样条的构造

令 \(h_j=x_{j+1}-x_j\). 定义样条函数如下\[ S_j(x)=a_j+b_j(x-x_j)+c_j(x-x_j)^2+d_j(x-x_j)^3,\quad j=0,1,\ldots,n-1.\]由连续性条件, \(f(x_j)=S_j(x_j)=a_j\) 且 \(a_{j+1}\) 满足\[ a_{j+1}=S_{j+1}(x_{j+1})=S_j(x_{j+1})=a_j+b_jh_j+c_jh_j^2+d_jh_j^3. \tag{10b}\]如果我们定义 \(a_n=f(x_n)\), 上面的方程对 \(j=0,1,\ldots,n-1\) 都成立. 由可微性条件可知,\[ b_{j+1}=S_{j+1}^\prime(x_{j+1})=S_{j}^\prime(x_{j+1})=b_j+2c_jh_j+3d_jh_j^2, \tag{10c}\]和\[ 2c_{j+1} = S_{j+1}^{\prime\prime}(x_{j+1})=S_{j}^{\prime\prime}(x_{j+1})=2c_j+6h_jd_j. \tag{10d}\]其中, \(j=0,1,\ldots, n-2.\) 如果我们定义 \(b_n=S^\prime(x_n)\) 和 \(c_n=S^{\prime\prime}(x_n)/2\), 方程 (10c,d) 对 \(n-1\) 同样成立.
下面, 我们考虑如何利用前面得到的方程来确定参数. 首先, 由方程 (10d) 可知 \(d_j=\frac{c_{j+1}-c_j}{3h_j}\). 代入 (10b)(10c) 可得两个新的方程\[\begin{align*} a_{j+1}&=a_j+b_jh_j+(2c_j+c_{j+1})\frac{h_j^2}{3},\\ b_{j+1}&=b_j+(c_j+c_{j+1})h_j.\end{align*}\tag{11}\]通过第一个方程 \(b_j\) 可以表示为\[ b_j = \frac{a_{j+1}-a_j}{h_j}-\frac{h_j^2}{3}(2c_j+c_{j+1}), \quad j=0,1,\ldots,n-1.\]将其代入到 (11) 中的第二个方程可得\[ \begin{bmatrix} h_{j-1} & 2(h_{j-1}+h_j) & h_j \end{bmatrix} \begin{bmatrix} c_{j-1}\\ c_j\\ c_{j+1} \end{bmatrix} = \frac{3}{h_j}(a_{j+1}-a_j)-\frac{3}{h_{j-1}}(a_j-a_{j-1}), \tag{12a}\]其中 \(j=1,2,\ldots,n-1\), 右边已知. 因此, 总共有 \(n-1\) 个方程和 \(n+1\) 个未知数. 所以, 我们还需要两个条件来唯一确定未知数 \(c_j\). 通过利用自然边界条件 \(S^{\prime\prime}(x_0) =S^{\prime\prime}(x_{n})=0\), 可得\[ c_0=0,\quad c_{n}=0.\tag{12b}\]方程 (12a,b) 构成一个矩阵方程, 其系数矩阵是三对角并且严格对角占优的, 所以存在唯一解. 因此, 我们可以唯一确定\(c_j,j=0,1,\ldots,n\); 然后可以确定 \(d_j,b_j\) 并最终确定整个三次样条多项式 \(S(x)\).

参考

[1] Burden, R. L., & Faires, J. D. (2010). Numerical Analysis. In Cengage Learning (9th ed.).
[2] 插值方法的基本概述和讨论.