一维椭圆边值问题的有限差分方法

2022年1月18日2022年1月18日 numanal 0 个评论有限差分, 椭圆边值问题, 离散Laplace算子

有限差分的基本思想

假设 \(\Omega\subset \mathbb{R}^n\) 为一个有界开集, 我们考虑如下的一般形式的边值问题\[\begin{align} \mathcal{L}u & = f \quad \text{在 } \Omega \text{ 上},\\ \mathcal{B}u & = g \quad \text{在 } \Gamma \text{ 上}.\end{align}\tag{1}\]其中 \(\mathcal{L}\) 是线性微分算子, \(\mathcal{B}\) 是一个指定边界条件的线性算子. 例如对于具有 Dirichlet 边界条件的 Laplace 方程\[ -\Delta u = f,\quad u=g,\]对应的两个算子分别为 \(\mathcal{L}:=-\Delta,\ \mathcal{B}:=\mathrm{id}\). 当然, 对于一个一般的二阶椭圆方程, 微分算子将相对复杂一些:\[ \mathcal{L}u:=-\sum_{i,j=1}^n \frac{\partial }{\partial x_j} \left( a_{ij}(x)\frac{\partial u}{\partial x_i} \right)+\sum_{i=1}^n b_i(x) \frac{\partial u}{\partial x_i} +c(x) u.\]

通常, 对于椭圆边值问题 (1), 有限差分方法 (Finite Difference Method) 的离散大致分为两个步骤:

选取有限个点 (网格点) 来近似区域 \(\Omega\), 这些点处的未知向量 \(U(x)\) 将成为函数 \(u(x)\) 在网格点上的近似值. 令 \(\bar{\Omega}_h := \Omega_h\cup \Gamma_h\) 为区域 \(\Omega\) 的一个网格划分, 其中 \(\Omega_h, \Gamma_h\) 分别是内部网格点和边界点的集合. 网格点之间的距离我们用 \(h\) 来表示, 通常称为网格大小.
利用差商算子 (Divided differences) 代替微分算子. 在这一步中, 我们事实上是在寻找逼近 (1) 的差分格式:
\[\begin{align} \mathcal{L}_hU(x) & = f(x) \quad x\in \Omega_h,\\ \mathcal{B}_hU(x) & = g(x) \quad x\in \Gamma_h.\end{align}\tag{2}\]如果离散问题 (2) 存在唯一解, 事实上是一个非奇异的线性系统或张量方程, 那么定义在网格点上的离散解 \(\left\{ U(x):x\in \bar{\Omega}_h \right\}\) 其实就是真解 \(\left\{ u(x):x\in \bar{\Omega}_h \right\}\) 的近似.

由上面的步骤可以看出, 有限差分方法的应用需要考虑如下问题: 1. 网格划分的实现; 2.差商算子的构造; 3. 误差与网格大小 \(h\) 的关系, 或者说当 \(h\to 0\) 时误差以什么样的速度趋于零. 我们将以椭圆方程为例来依次回答上述问题, 其中用到的材料大部分来自 [1].

一维空间中的基本符号定义

网格

考虑区间 \((0,1)\) 上的一致网格 (步长为 \(h\)):\[ \bar{\Omega}_h:=\Omega_h\cup \Gamma_h:=\left\{ x_i=ih:\ i=1,\ldots, N-1 \right\}\cup \left\{ x_0=0,x_N=1 \right\}.\]其中, \(N>2\) 表示网格点个数的整数. 下面, 每个网格点 \(x_i\) 对应一个未知量 \(V_i:=V(x_i)\), 它们构成的线性空间记为 \(S_h\), 事实上, 我们有 \(S_h \equiv \mathbb{R}^{N+1}\); 类似地, 边值为零的子空间记为 \(S_h^0=\left\{ V\in S_h:\ V_0=V_N=0 \right\}\equiv \mathbb{R}^{N-1}\).

有了线性空间, 我们还需要定义相应的范数, 这个范数会成为衡量离散解与真解之间误差的一个标准. 令 \(S_h^0\) 上的内积和范数定义为\[ (V,W)_h := \sum_{x\in \Omega_h} h V_i W_i,\quad \|V\|_h=(V,V)_h^{1/2}.\]类似地, 我们定义包含端点的内积和范数\[ [V,W]_h := \sum_{x\in \bar{\Omega}_h} h V_i W_i,\quad \|V\|_h=[V,V]_h^{1/2}.\]

离散 Laplace 算子

我们引入常用的差商算子. 首先, 对于一阶导数我们有前向、后向和中心差商算子\[ D_x^+V := \frac{V(x+h)-V(x)}{h},\quad D_x^-V := \frac{V(x)-V(x-h)}{h},\quad D_x^0V:=\frac{1}{2} \left( D_x^+V+D_x^-V \right).\]给定集合 \(S_h^0\), 离散的 Laplace 算子 \(\Lambda:S_h^0\to S_h^0\) 定义如下\[ \Lambda V:=\begin{cases} -D_x^+D_x^- V & x\in \Omega_h,\\ 0& x\in \Gamma_h. \end{cases}\]

引理 1 (对称正定). 算子 \(\Lambda:S_h^0\to S_h^0\) 对称正定, 并且满足\[ (\Lambda V,W)_h=(-D_x^+D_x^- V, V)_h = \sum_{i=1}^N h |D_x^-V_i|^2 = \sum_{i=0}^{N-1} h |D_x^+V_i|^2. \tag{3}\]

证明. 事实上, 对任意向量 \(V,W\in S_h^0\), 令 \(U_i = D_x^-V_i, i=1,\ldots,N\)\[\begin{align*} (\Lambda V,W)_h &= -\sum_{i=1}^{N-1} h\frac{U_{i+1}-U_i}{h} W_i \\ &= -h \frac{U_{N}}{h}W_{N-1}+\sum_{i=2}^{N-1} h\frac{W_{i}-W_{i-1}}{h} U_i + h\frac{U_1}{h}W_1\\ &= h U_N\frac{W_N-W_{N-1}}{h}+\sum_{i=1}^{N-1} hU_i\frac{W_{i}-W_{i-1}}{h} \\ &= h D_x^-V_N D_x^-W_N+ (D_x^-V, D_x^-W)_h.\end{align*}\]另一方面, 利用 \(D_x^-V_i=D_x^+V_{i-1},i=1,\ldots,N\) 可得\[\begin{align*} (\Lambda V,W)_h &= -h \frac{U_{N}}{h}W_{N-1}+\sum_{i=1}^{N-2} h\frac{W_{i+1}-W_{i}}{h} U_{i+1} + h\frac{U_1}{h}W_1\\ &= h D_x^+V_{N-1}D_x^+W_{N-1}+\sum_{i=1}^{N-2} hD_x^+V_iD_x^+W_i + hD_x^+V_0D_x^+W_0 \\ &= (D_x^+V, D_x^+W)_h +hD_x^+V_0D_x^+W_0.\end{align*}\]上面两个等式中的结果是对称的, 所以我们可以回溯推导过程, 得到如下对称性质:\[ \begin{align*} (\Lambda V,W)_h&=(V,\Lambda W)_h \\ &= (D_x^-V, D_x^-W)_h +h D_x^-V_N D_x^-W_N\\ &= hD_x^+V_0D_x^+W_0+(D_x^+V, D_x^+W)_h. \end{align*} \tag{4}\]为得到 \(\Lambda\) 的正定性质, 只需在上面的等式中令 \(W=V\), 从而得到\[ (\Lambda V,V)_h = \|D_x^-V\|_h^2 +h| D_x^-V_N|^2 =h|D_x^+V_0|^2+\|D_x^+V\|_h^2.\tag{5}\]利用 (5) 可知, 对任意 \(V\in S_h^0\), \((\Lambda V,V)_h=0\) 当且仅当 \(V=0\). 因此如下严格正定性成立\[ (\Lambda V,V)_h>0,\quad \forall 0\neq V\in S_h^0. \tag{6}\]\(\heartsuit\)

范数

由于 \(\Lambda\) 是有限维空间 \(S_h^0\equiv \mathbb{R}^{N-1}\) 上的对称正定算子, 它一定有 \(N-1\) 个正的特征值 \(\lambda_k\) 和相应的特征向量 \(V^k\) 满足特征方程\[ \Lambda V^k = \lambda_k V^k, \quad k=1,\ldots ,N-1.\]其中, \(V^k\) 构成线性空间 \(S_h^0\) 的一组标准正交基, 即 \((V^k,V^l)_h=\delta_{kl}\). 关于严格的证明请参考 [3, Sec 2.4.2] 或者附录. 由正交基的性质可以得到如下结果:

线性展开 \(V=\sum_{i=1}^{N-1}c_k V^k\), 其中 \(c_k=(V,V^k)_h\);
离散的 Parseval 等式 \(\|V\|_h^2 = \sum_{i=1}^{N-1} c_k^2\).
\((\Lambda V,V)_h= \sum_{i=1}^{N-1} \lambda_k c_k^2 \);
\(\|\Lambda V\|_h^2=(\Lambda V, \Lambda V)_h= \sum_{i=1}^{N-1} \lambda_k^2 c_k^2\).

由 2)3) 可知 (离散 Friedrichs 不等式)\[ \sum_{i=1}^N h |D_x^-V_i|^2 = \sum_{i=0}^{N-1} h |D_x^+V_i|^2=(\Lambda V,V)_h \geq \lambda_1 \|V\|_h^2;\]由 3)4) 可知 (\(\lambda_1=\min_k \lambda_k>8\), 见附录)\[ \|\Lambda V\|_h^2 \geq \min_k \lambda_k (\Lambda V,V)_h \geq \lambda_1^2 \|V\|_h^2.\]如果我们定义如下范数:\[\begin{align*} |V|_{1,h}^2 &:= \sum_{i=1}^N h |D_x^-V_i|^2 = \sum_{i=0}^{N-1} h |D_x^+V_i|^2, \\ |V|_{2,h} &:= \|\Lambda V\|_h= \|D_x^+D_x^- V\|_h , \\ \|V\|_{k,h}^2 &:= \|V\|_{k-1,h} + |V|_{k,h}, \quad k=1,2.\end{align*}\]可以得到如下离散 Friedrichs 不等式\[ \|V\|_{1,h}^2 \leq \left( 1+\frac{1}{\lambda_1} \right) |V|_{1,h}^2, \tag{7}\]其中 \(\lambda_1=\min_k \lambda_k>0\) 为 \(\Lambda\) 的最小特征值, 并且由附录可知, \(\lambda_1\) 的下界关于步长是稳定的 (不随之变小而变小).

一维模型问题

考虑如下的两点边值问题\[ -u^{\prime\prime}(x)+c(x)u(x)=f, \ x\in (0,1); \quad u(0)=(1)=0, \tag{8}\]其中 \(0\leq c \in L^\infty(0,1)\), \(f\in H^{-1}(0,1)\). 我们引入一维问题的初衷在于系统介绍有限差分方法的基本框架.

有限差分格式

通过利用二阶差商公式我们可以将方程 (3) 写成如下离散形式\[\begin{align*} &-D_x^+D_x^-u(x_i)+c(x_i)u(x_i)\approx f(x_i),\quad i=1,2,\ldots,N-1,\\ &u(x_0)=0,\quad u(x_N)=0.\end{align*} \tag{9a}\]如果令 \(U_i=u(x_i)\), 上述问题等价为: 寻找 \(U\in S_h^0\) 满足方程\[ KU=F, \tag{9b}\]\[ K=\begin{bmatrix} \frac{2}{h^2}+c(x_1) & -\frac{1}{h^2} & & & 0\\ -\frac{1}{h^2} & \frac{2}{h^2}+c(x_2) &-\frac{1}{h^2} & & \\ & \ddots & \ddots & \ddots & & \\ & &-\frac{1}{h^2} & \frac{2}{h^2}+c(x_{N-2}) &-\frac{1}{h^2} \\ & & &-\frac{1}{h^2} & \frac{2}{h^2}+c(x_{N-1}) \end{bmatrix}\]\[ U=(U_1, U_2, \ldots, U_{N-1}),\quad F=(f(x_1), f(x_2), \ldots, f(x_{N-1})).\]

稳定性分析

定理 1 (存在唯一性). 如果 \(c,f\) 是定义在 \((0,1)\) 上的连续函数并且 \(c\geq 0\), 那么有限差分方法 (9) 有且只有唯一解 \(U\in S_h^0\); 并且满足如下的稳定性质\[ \|U\|_{1,h} \leq \left( 1+\frac{1}{\lambda_1} \right) \|f\|_{h}, \tag{10}\]其中, \(\|f\|_{h}^2=\sum_{i=1}^{N-1}h|f(x_i)|^2\) 且 \(\lambda_1\) 与步长 \(h\) 无关.

证明. 对于唯一性, 只需要说明当函数 \(f= 0\) 时线性系统 (9) 只有零解. 回忆条件 \(c\geq 0\), 将方程 (9) 关于 \(U\) 做内积可得\[\begin{align*} 0=(-D_x^+D_x^-U,U)_h + (cU,U)_h \geq \sum_{i=1}^N h |D_x^-U_i|^2,\end{align*}\]即 \(D_x^-U_i=0, i=1,2,\ldots,N\). 由 \(D_x^-U_i=\frac{U_i-U_{i-1}}{h}\) 和边值条件 \(U_0=U_N=0\) 可得 \(U=0\). 或者可以直接利用离散 Laplace 算子的正定性 (引理 1) 也可得到如下唯一性\[ 0=(\Lambda U,U)_h+ (cU,U)_h \geq (\Lambda U,U)_h \geq 0\quad \Leftrightarrow \quad U=0.\] 下面证明稳定性估计 (10). 利用离散 Friedrichs 不等式 (7) 可得\[\begin{align*} \|U\|_{1,h}^2 &\leq \left( 1+\frac{1}{\lambda_1} \right) |U|_{1,h}^2 \\ &=\left( 1+\frac{1}{\lambda_1} \right) (-D_x^+D_x^-U,U)_h,\\ &\leq \left( 1+\frac{1}{\lambda_1} \right) (-D_x^+D_x^-U+cU,U)_h,\\ &= \left( 1+\frac{1}{\lambda_1} \right) (f,U)_h,\\ &\leq \left( 1+\frac{1}{\lambda_1} \right) \|f\|_{h} \|U\|_{1,h},\end{align*}\]从而得到 \(\|U\|_{1,h}\leq \left( 1+\frac{1}{\lambda_1} \right) \|f\|_{h}\). \(\heartsuit\)

下面我们来看一下如何得到有限差分方法的收敛性.

定理 2 (收敛性). 令 \(c,f\) 是定义在 \((0,1)\) 上的连续函数并且 \(c\geq 0\); 并且假设 \(u\in C^4[0,1]\); 那么有限差分方法满足如下收敛性估计\[ \|u-U\|_{1,h} \leq \left( 1+\frac{1}{\lambda_1} \right) \frac{\|u\|_{C^4[0,1]}}{12}h^2.\tag{11}\]

证明. 首先, 定义误差\[ E_i = u(x_i)-U_i, \quad i=0,1,\ldots ,N.\]将解析解满足的方程 \(-u^{\prime\prime}+cu=f\) 与差分格式 (9) 做减法可得\[\begin{align*} 0&=\left( -u^{\prime\prime}(x_i)+cu(x_i) \right)-\left( -D_x^+D_x^-U_i+cU_i \right)\\ &= -D_x^+D_x^-E_i + c E_i + R_i,\end{align*}\]其中 \(R_i:=-u^{\prime\prime}(x_i)+D_x^+D_x^-u(x_i)\) 通常称为截断误差或相容性误差. 由定理 1 中稳定性的分析过程可知, 误差 \(E\) 满足如下估计\[ \|E\|_{1,h} \leq \left( 1+\frac{1}{\lambda_1} \right) \|R\|_{h}. \tag{12a}\]所以, 我们后面需要考虑对截断误差的估计. 由二阶导数的差分逼近性质可知 [2, Section 4.1]\[ R_i=-u^{\prime\prime}(x_i)+\frac{U_{i+1}-2U_i+U_{i-1}}{h^2} = \frac{h^2}{12}u^{(4)}(\xi), \quad \xi \in (x_{i}-h,x_i+h),\]当然我们必须假设 \(u\in C^4[0,1]\). 因此, 容易得到如下误差估计\[ \|R\|_{h}=\left( \sum_{i=1}^{N-1} hR_i^2 \right)^{1/2} \leq \frac{h^2}{12} \|u\|_{C^4[0,1]}. \tag{12b}\]综合 (12a)(12b) 两个不等式即完成证明. \(\heartsuit\)

数值算例

例 1. 考虑如下二阶椭圆边值问题:\[ -u^{\prime\prime}+2u=f, \quad x\in (0,\pi),\]我们令解析解为 \(u(x)=\sin(x)\). 附录中给出了 Python 实现, 其计算的误差结果如下:

N       error
5       1.3713e-02
10      3.4341e-03
20      8.5889e-04
40      2.1474e-05
80      5.3688e-05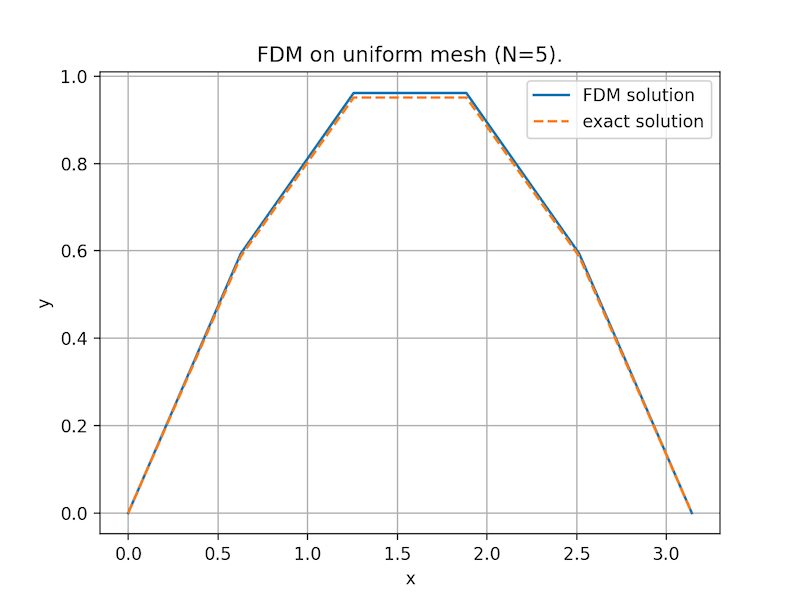

参考

[1] Jovanović, B. S., & Süli, E. (2014). Analysis of Finite Difference Schemes. In Finite Difference Schemes and Partial Differential Equations.
[2] Burden, R. L., & Faires, J. D. (2010). Numerical Analysis. In Cengage Learning (9th ed.).
[3] Samarskii, Alexander A. The Theory of Difference Schemes. Vol. 240. CRC Press, 2001.
[4] 一维波方程的有限差分方法.

附录:

离散 Laplace 算子的特征值

本节内容参考 [3, Sec 2.4.2]. 在讨论离散算子的特征值问题之前, 我们先来考虑连续的特征值问题:\[ -u^{\prime\prime}(x)=\lambda u(x), \quad 0< x < L, \quad u(0)=u(L)=0.\tag{13}\]满足上述方程的非平凡解 \((\lambda,u)\) 称为 (13) 的特征值和特征函数, 并且满足

\(\lambda_k=\frac{k^2\pi^2}{L^2},\ u_k(x)=\sqrt{\frac{2}{L}}\sin \frac{k\pi x}{L},\ k=1,2,\ldots\)
所有特征函数构成一组规范正交系:
\[ \int_{0}^1u_k(x)u_m(x)dx=\delta_{km}.\]

方程 (13) 对应的有限差分格式为\[\begin{align*} &-D_x^+D_x^-u(x_i)=\lambda u(x_i),\quad i=1,2,\ldots,N-1,\\ &u(x_0)=0,\quad u(x_N)=0.\end{align*}\]即寻找 \(\lambda\) 和非零向量 \(U\in S_h^0\) 满足方程\[ KU=DU,\tag{14}\]其中 \(U=(U_1, U_2, \ldots, U_{N-1})\),\[ K=\begin{bmatrix} \frac{2}{h^2} & -\frac{1}{h^2} & & & 0\\ -\frac{1}{h^2} & \frac{2}{h^2} &-\frac{1}{h^2} & & \\ & \ddots & \ddots & \ddots & & \\ & &-\frac{1}{h^2} & \frac{2}{h^2} &-\frac{1}{h^2} \\ & & &-\frac{1}{h^2} & \frac{2}{h^2} \end{bmatrix}, \quad D = \lambda \begin{bmatrix} 1 & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \\ \end{bmatrix}.\]

我们希望找到类似连续特征值问题的解, 即寻找具有如下形式的特征函数\[ U_i = \sin \alpha x_i, \quad i=1,2,\ldots, N-1,\]其中 \(\alpha\) 是待定参数. 将上式代入等式 (14) 并利用三角和差化积公式可得\[\begin{align*} 0&=-\sin \alpha x_{i-1} + (2-\lambda h^2) \sin \alpha x_i – \sin \alpha x_{i+1} \\ &= (2-\lambda h^2) \sin \alpha x_i – 2 \sin \alpha x_i \cos \alpha h.\end{align*}\]因为我们要寻找的解 \(U\) 不恒为零, 所以上面的等式表明\[ 0=(2-\lambda h^2)-2 \cos \alpha h\quad \Rightarrow \quad \lambda = \frac{2-2 \cos \alpha h}{h^2} = \frac{4}{h^2}\sin ^2 \frac{\alpha h}{2}\]下面我们来确定 \(\alpha\) 的值. 我们可以利用的条件是: 选取 \(\alpha\) 使得边值为零\[ U_0 = \sin \alpha 0=0,\quad U_N =\sin \alpha L = 0.\]第一个条件自动满足, 使第二个条件成立的值有 \(\alpha=\alpha_k=\frac{k\pi}{L},k=1,2,\ldots,N-1\). 因此, 我们就找到了离散 Laplace 算子在区间 \((0,L)\) 上的特征值和特征向量, 即 \(\Lambda U^k = \lambda_k U^k\), 其中\[ \lambda_k=\frac{4}{h^2}\sin ^2 \frac{k\pi h}{2L},\quad U^k_i = \sin \frac{k\pi x_i}{L},\quad i=1,2,\ldots,N-1.\]

我们总结如下性质:

特征值从小到大排列如下:\[ 0 < \lambda_1 = \frac{4}{h^2}\sin ^2 \frac{\pi h}{2L} \leq \cdots < \lambda_{N-1} = \frac{4}{h^2}\sin ^2 \frac{(N-1)\pi h}{2L}.\]如果 \(h\to 0\), 利用极限 \(\lim_{x\to 0}\frac{\sin x}{x}=1\) 可知\[ \lambda_k=\frac{4}{h^2}\sin ^2 \frac{k\pi h}{2L} =\frac{\pi^2}{L^2}\left( \frac{2L}{k\pi h} \right)^2\sin ^2 \frac{k\pi h}{2L} \to \frac{k^2\pi^2}{L^2}. \tag{15a}\]我们只关心最小的特征值随步长大小的变化情况. 当 \(L=1\) 时, 步长 \(h\) 足够小的话就有 \[ \lambda_1\to \pi^2>8. \tag{15b}\]实际上, 容易验证, 只要当 \(h<0.5\), 就有上式成立.
特征向量 \(U^k\) 相互正交, 事实上当 \(k\neq m\) 时 \[ 0= (\Lambda U^k, U^m)_h-(U^k,\Lambda U^m)_h = (\lambda_k-\lambda_m)(U^k,U^m)_h.\]因为 \(\lambda_k\neq \lambda_m\), 所以必有正交关系成立.
\(\|U^k\|_h=\sqrt[]{L/2}\). 证明如下.\[ \|U^k\|_h^2=\sum_{j=1}^{N-1} h \sin^2 \frac{k\pi x_j}{L} =\sum_{j=1}^{N-1} \frac{h}{2} \left( 1-\cos \frac{2k\pi x_j}{L} \right).\]利用 \(x_j=jh\) 可知下面的等式成立\[ \begin{align*} \sum_{j=1}^{N-1} \cos \frac{2k\pi x_j}{L} &=\Re\sum_{j=1}^{N-1} e^{i\frac{2k\pi x_j}{L}} =\Re\sum_{j=1}^{N-1} \left[ e^{i\frac{2k\pi h}{L}} \right]^j \\ &=\Re e^{i\frac{2k\pi h}{L}} \frac{1-e^{i\frac{2k\pi h(N-1)}{L}}}{1-e^{i\frac{2k\pi h}{L}}}=-1. \end{align*}\]代入原式可得\[ \|U^k\|_h^2=(N-1)h/2+h/2=Nh/2=L/2.\]

数值实验的 Python 实现

# FDM on uniform mesh for 1d elliptic problem:
#       -u''+c*u = f on (0,pi)
# with u=sin(x).
# 
# --- by numanal.com, 2022/1/17
# 
import numpy as np
from scipy.sparse import diags
from scipy.sparse.linalg import spsolve
import matplotlib.pyplot as plt

class FDM1D(object):
    def __init__(self, x_span, N, pde_c, pde_f, bdy_values, pde_u):
        self.x_span = x_span
        self.N = N
        self.u_fdm = pde_u

        self.pde_c = pde_c
        self.pde_f = pde_f
        self.pde_bdy_values = bdy_values
        self.pde_u = pde_u
        
    def run(self):
        # solve
        self.u_fdm = np.zeros(N+1)
        self.u_fdm[0] = self.pde_bdy_values[0]
        self.u_fdm[-1] = self.pde_bdy_values[1]
        h = (self.x_span[1]-self.x_span[0])/N
        x = np.linspace(self.x_span[0], self.x_span[1],N+1,endpoint=True)

        D = np.ones(N-1)*2 + h**2*self.pde_c(x[1:-1])
        trivec = [ D, -np.ones(N-2), -np.ones(N-2) ]
        K = diags(trivec, [0,-1,1])

        F= h**2 * self.pde_f(x[1:-1])
        F[0] += self.pde_bdy_values[0]
        F[-1] += self.pde_bdy_values[1]
        self.u_fdm[1:-1] = spsolve(K,F)

        # l2 norm: (sum h|e_i|^2)^{1/2}
        print(np.linalg.norm( self.u_fdm-self.pde_u(x) )*h**(1/2))

        # plot
        fig = plt.figure()
        ax = fig.add_subplot(1, 1, 1)
        ax.plot(x, self.u_fdm, '-', label='FDM solution')
        ax.plot(x, self.pde_u(x), '--', label='exact solution')
        plt.xlabel('x')
        plt.ylabel('y')
        plt.title('FDM on uniform mesh (N=5).')
        plt.legend()
        plt.grid(True)
        plt.show()


def pde_u(x):
    return np.sin(x)

def pde_c(x):
    return np.ones(x.shape[0])*2

def pde_f(x):
    return np.sin(x)+pde_c(x)*pde_u(x)


if __name__=='__main__':
    
    x_span = np.array([0., np.pi])
    bdy_values = pde_u(x_span)
    N = 80

    # solve and print sol
    solver = FDM1D(x_span=x_span, N=N, pde_c=pde_c, pde_f=pde_f, bdy_values=bdy_values, pde_u=pde_u)
    
    solver.run()

分享到: