DistMesh – 一个简单的 MATLAB 网格生成工具

2021年9月27日2022年3月28日 numanal 0 个评论 distmesh, 网格生成

关于 DistMesh

DistMesh 是一个简单的 MATLAB 和 GNU Octave 代码，用于自动生成非结构化 2D 三角形和 3D 四面体网格。
该库可以从图形用户界面 (GUI) 中与 FEATool Multiphysics Octave 和 MATLAB PDE and FEM Toolbox 一起使用。
DistMesh 版本的 Julia 实现也可在 DistMesh-Julia 存储库以及 QuadMesh（基于距离函数的非结构化四边形网格生成）中找到。

描述

DistMesh 算法是由麻省理工学院数学系的 Per-Olof Persson 和 Gilbert Strang 发明的。有关原始 DistMesh 方法和 MATLAB 网格生成代码的更详细说明，请参见 SIAM 评论论文和以下链接的其他参考资料。

DistMesh 算法的简单性是由于使用带符号距离函数（水平集）来指定和描述要网格化的域、几何形状和区域。距离函数指定空间中任意点到域边界的最短距离，其中函数的符号在区域外为正，在内为负，边界上为零。此定义用于识别点是位于几何图形内部还是外部。此外，距离函数的梯度指向边界的方向，允许外部的点有效地移回域。

一个简单的例子是二维单位圆，其距离函数为 d(r) = r-1，其中 r = sqrt(x^2+y^2) 是距原点的距离。对于更复杂的几何，距离函数可以通过网格上的值之间的插值来计算，这是水平集方法的常见表示。

对于网格生成程序，DistMesh 使用 MATLAB 和 Octave 中的 Delaunay 三角剖分程序，并尝试通过基于力的平滑程序优化节点位置。 Delaunay 定期更新拓扑。边界点只允许通过使用距离函数的投影与边界相切移动。这种迭代过程通常会产生非常均匀且形状良好的高质量网格。

用法

要使用此网格生成代码，只需下载独立的 distmesh 源代码并在 MATLAB 或 Octave 中运行它。函数语法如下

[ P, T, STAT ] = DISTMESH( FD, FH, H0, BBOX, P_FIX, E_FIX, IT_MAX, FID, FIT)

其中 FD 是几何描述的函数句柄，应将评估坐标和点作为输入。例如 fd = @(p) sqrt(sum(p.^2,2)) - 1; 指定单位圆的距离函数（支持函数句柄、字符串函数名和匿名函数）。与 FD 类似，FH 是一个描述所需相对网格尺寸分布的函数。例如 fh = @(p)ones(size(p,1),1); 指定均匀分布，其中 FH 在所有点的计算结果为 1。 H0 是指定初始边缘长度的数字标量，BBOX 是域的 2 x 2（或 3D 中的 2 x 3）边界框（包含 FD 的零轮廓/水平集）。 P_FIX 可选地指定在生成的网格中应始终存在（固定）的点数。 E_FIX 可以是要约束的边顶点索引集，也可以是具有要调用的函数句柄的元胞数组。 IT_MAX 设置允许的最大网格生成迭代次数（默认为 1000）。最后，FID 指定用于输出的文件标识（默认 1 = 终端输出），FIT 是一个可选的 % 函数，用于调用每次迭代以检查是否提前终止。

DistMesh MATLAB 函数返回 P 中的网格点顶点、T 中的三角化单纯形以及可选的统计结构 STAT，包括计时和收敛信息。

输入参数:

       FD:        Distance function d(x,y,(z))
       FH:        Scaled edge length function h(x,y,(z))
       H0:        Initial edge length
       BBOX:      Bounding box [xmin,ymin,(zmin); xmax,ymax,(zmax)]
       P_FIX:     Fixed node positions (N_P_FIX x 2/3)
       E_FIX:     Constrained edges (N_E_FIX x 2)
       IT_MAX:    Maximum number of iterations
       FID:       Output file id number (default 1 = terminal)

输出参数:

       P:         Grid vertex/node coordinates (N_P x 2/3)
       T:         Triangle indices (N_T x 3)
       STAT:      Mesh generation statistics (struct)

例子

Example 1: Uniform mesh on unit circle

fd = @(p) sqrt(sum(p.^2,2)) - 1;
fh = @(p) ones(size(p,1),1);
[p,t] = distmesh( fd, fh, 0.2, [-1,-1;1,1] );
patch( 'vertices', p, 'faces', t, 'facecolor', [.9, .9, .9] )

Example 2: Uniform mesh on ellipse

fd = @(p) p(:,1).^2/2^2 + p(:,2).^2/1^2 - 1;
fh = @(p) ones(size(p,1),1);
[p,t] = distmesh( fd, fh, 0.2, [-2,-1;2,1] );
patch( 'vertices', p, 'faces', t, 'facecolor', [.9, .9, .9] )

Example 3: Uniform mesh on unit square

fd = @(p) -min(min(min(1+p(:,2),1-p(:,2)),1+p(:,1)),1-p(:,1));
fh = @(p) ones(size(p,1),1);
[p,t] = distmesh( fd, fh, 0.2, [-1,-1;1,1], [-1,-1;-1,1;1,-1;1,1] );
patch( 'vertices', p, 'faces', t, 'facecolor', [.9, .9, .9] )

Example 4: Uniform mesh on complex polygon

pv = [-0.4 -0.5;0.4 -0.2;0.4 -0.7;1.5 -0.4;0.9 0.1;
        1.6 0.8;0.5 0.5;0.2 1;0.1 0.4;-0.7 0.7;-0.4 -0.5];
fd = { 'l_dpolygon', [], pv };
fh = @(p) ones(size(p,1),1);
[p,t] = distmesh( fd, fh, 0.1, [-1,-1; 2,1], pv );
patch( 'vertices', p, 'faces', t, 'facecolor', [.9, .9, .9] )

Example 5: Rectangle with circular hole, refined at circle boundary

drectangle = @(p,x1,x2,y1,y2) -min(min(min(-y1+p(:,2),y2-p(:,2)),-x1+p(:,1)),x2-p(:,1));
fd = @(p) max( drectangle(p,-1,1,-1,1), -(sqrt(sum(p.^2,2))-0.5) );
fh = @(p) 0.05 + 0.3*(sqrt(sum(p.^2,2))-0.5);
[p,t] = distmesh( fd, fh, 0.05, [-1,-1;1,1], [-1,-1;-1,1;1,-1;1,1] );
patch( 'vertices', p, 'faces', t, 'facecolor', [.9, .9, .9] )

Example 6: Square, with size function point and line sources

dcircle = @(p,xc,yc,r) sqrt((p(:,1)-xc).^2+(p(:,2)-yc).^2)-r;
fd = @(p) -min(min(min(p(:,2),1-p(:,2)),p(:,1)),1-p(:,1));
dpolygon = @(p,v) feval('l_dpolygon',p,v);
fh = @(p) min(min(0.01+0.3*abs(dcircle(p,0,0,0)), ...
                    0.025+0.3*abs(dpolygon(p,[0.3,0.7;0.7,0.5;0.3,0.7]))),0.15);
[p,t] = distmesh( fd, fh, 0.01, [0,0;1,1], [0,0;1,0;0,1;1,1] );
patch( 'vertices', p, 'faces', t, 'facecolor', [.9, .9, .9] )

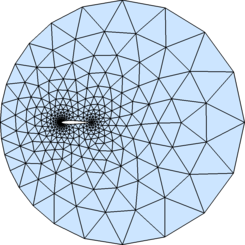
Example 7: NACA0012 airfoil

hlead = 0.01; htrail = 0.04; hmax = 2; circx = 2; circr = 4;
a = 0.12/0.2*[0.2969,-0.126,-0.3516,0.2843,-0.1036];
fd = @(p) max( dcircle(p,circx,0,circr), ...
                -((abs(p(:,2))-polyval([a(5:-1:2),0],p(:,1))).^2-a(1)^2*p(:,1)) );
fh = @(p) min(min(hlead+0.3*dcircle(p,0,0,0),htrail+0.3*dcircle(p,1,0,0)),hmax);

fixx = 1 - htrail*cumsum(1.3.^(0:4)');
fixy = a(1)*sqrt(fixx) + polyval([a(5:-1:2),0],fixx);
pfix = [[circx+[-1,1,0,0]*circr; 0,0,circr*[-1,1]]'; 0,0; 1,0; fixx,fixy; fixx,-fixy];
bbox = [circx-circr,-circr; circx+circr,circr];
h0   = min([hlead,htrail,hmax]);
[p,t] = distmesh( fd, fh, h0, bbox, pfix );
patch( 'vertices', p, 'faces', t, 'facecolor', [.9, .9, .9] )

Example 8: Uniform mesh on unit sphere

fd = @(p) sqrt(sum(p.^2,2)) - 1;
fh = @(p) ones(size(p,1),1);
[p,t] = distmesh( fd, fh, 0.2, [-1,-1,-1;1,1,1] );
f = [t(:,[1:3]); t(:,[1,2,4]); t(:,[2,3,4]); t(:,[3,1,4])];
patch( 'vertices', p, 'faces', f, 'facecolor', [.9, .9, .9] )

Example 9: Uniform mesh on unit cube

fd = @(p) -min(min(min(min(min(p(:,3),1-p(:,3) ),p(:,2)),1-p(:,2)),p(:,1)),1-p(:,1));
fh = @(p) ones(size(p,1),1);
pfix = [-1,-1,-1;-1,1,-1;1,-1,-1;1,1,-1; -1,-1,1;-1,1,1;1,-1,1;1,1,1];
[p,t] = distmesh( fd, fh, 0.2, [-1,-1,-1;1,1,1], pfix );
f = [t(:,[1:3]); t(:,[1,2,4]); t(:,[2,3,4]); t(:,[3,1,4])];
patch( 'vertices', p, 'faces', f, 'facecolor', [.9, .9, .9] ), view(3)

Example 10: Uniform mesh on cylinder

fd = @(p) -min(min(p(:,3),4-p(:,3)),1-sqrt(sum(p(:,1:2).^2,2)));
fh = @(p) ones(size(p,1),1);
pfix = [-1,-1,-1;-1,1,-1;1,-1,-1;1,1,-1; -1,-1,1;-1,1,1;1,-1,1;1,1,1];
[p,t] = distmesh( fd, fh, 0.5, [-1,-1,0;1,1,4], [] );
f = [t(:,[1:3]); t(:,[1,2,4]); t(:,[2,3,4]); t(:,[3,1,4])];
patch( 'vertices', p, 'faces', f, 'facecolor', [.9, .9, .9] ), view(3)