声波传输的数学模型

模型构建

我们考虑理想流体中的小振幅声波的数学模型. 小振幅声波的基本条件:

• 压强变化远小于静态声压, 即 \(\Delta P\ll P_0\);
• 质点速度远小于声速, 即 \(\mathbf{v}\ll c\);
• 质点位移远小于声波波长, 即 \(\mathbf{u}\ll \lambda\);
• 媒质密度变化远小于静态密度, 即 \(\Delta \rho \ll \rho_0\);

为了推导出波方程, 我们需要利用相关的质量守恒、动量守恒和能量守恒关系.

连续性方程 (conservation of mass)

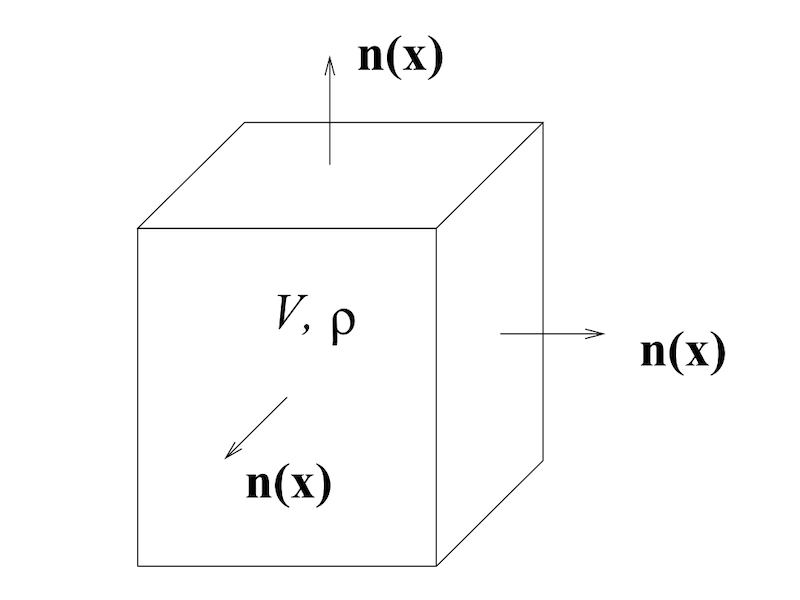
考虑流体的流动模型, 其压力 \(P(x,t)\), 密度 \(\rho(x,t)\), 速度 \(\mathbf{v}(x,t)\). 假设 \(V\) 为一个空间体元, 其边界为 \(\partial V\), 外法向量为 \(\mathbf{n}\). 那么, 单位时间内的质量守恒关系可以表示如下\[ -\frac{\partial }{\partial t} \int_{V}\rho dV = \int_{\partial V} \rho (\mathbf{v}\cdot \mathbf{n}) dS,\]即体元 \(V\) 中单位时间内的质量变化等于流体通过边界流出 (或流入) 的质量. 通过 Gauss 定理可以将上式中的面积分转变为体积分:\[ -\frac{\partial }{\partial t} \int_{V}\rho dV = \int_{V} \nabla\cdot (\rho \mathbf{v}) dV.\]从而得到连续性方程:\[ \frac{\partial \rho}{\partial t} + \nabla\cdot (\rho \mathbf{v})=0. \tag{1}\]

运动方程 (conservation of momentum)

考虑体元上的牛顿第二定律 \(\mathbf{F}=m \mathbf{a}\):\[ -\int_{\partial V}P \mathbf{n}dS = \int_{V}\rho \frac{d\mathbf{v}}{dt} dV\]再次利用 Gauss 定理将面积分转变成体积分可得\[ -\int_{V}\nabla P dS = \int_{V}\rho \frac{d\mathbf{v}}{dt} dV.\]由于声波是微小振动, 所以全微分可以由偏微分来近似 (线性化) \(\frac{d\mathbf{v}}{dt}\approx \frac{\partial \mathbf{v}}{\partial t}\). 从而可以得到如下的运动方程 (Euler 方程)\[ \rho \frac{\partial \mathbf{v}}{\partial t} =- \nabla P. \tag{2}\]

物态方程 (conservation of energy)

理想流体中声波的传播过程可以看作是一个绝热的过程, 不会发生热交换, 从而可以认为压强 \(P\) 只是密度 \(\rho\) 的函数, 并且满足条件\[ dP = \frac{d P}{d \rho} d \rho= c^2 d \rho,\]其中, \(c\) 代表波速, 只与媒质有关. 从而可得如下物态方程:\[ P= c^2 \rho. \tag{3}\]

波方程

由小振幅假设可知, 方程 (1)(2) 可以写成\[ \frac{\partial \rho}{\partial t} + \rho_0\nabla\cdot \mathbf{v}=0, \quad \rho_0 \frac{\partial \mathbf{v}}{\partial t} =- \nabla P.\]利用 (3) 可得如下一阶抛物方程\[\begin{align} \frac{\partial P}{\partial t} + c^2\rho_0\nabla\cdot \mathbf{v}&=0, \\ \frac{\partial \mathbf{v}}{\partial t} + \rho_0^{-1}\nabla P &=0.\end{align} \tag{4}\]其对应的二阶方程为\[ \frac{\partial ^2 P}{\partial t^2} – c^2 \rho_0 \nabla\cdot \left( \rho_0^{-1}\nabla P \right) = 0. \tag{5}\]利用 Fourier 变换或者令 \(P(x,t)=p(x)e^{-i\omega t}\), 我们可以得到时谐波方程, 即 Helmholtz 方程:\[ -\Delta p – k^2 p = 0,\quad k=\frac{\omega}{c}.\]

抽象数学模型

大部分波动方程, 声波或者电磁波, 都可以写成一阶和二阶两种数学形式, 正如 (4)(5) 两种形式. 一般来说, 考虑一阶方程\[\begin{align*} \frac{\partial u}{\partial t} – \mathcal{B} v &=0,\\ \frac{\partial v}{\partial t} + \mathcal{B}^* u &=0,\end{align*} \tag{6}\]其中, \(u:\Omega\to \mathbb{R}^p\) 和 \(v:\Omega\to \mathbb{R}^q\) 是定义在区域 \(\Omega\subset \mathbb{R}^n\) 上的未知量, \(\mathcal{B}, \mathcal{B}^*\) 是关于某个加权的内积空间 \(H\) 共轭的线性算子.

通过消去其中一个变量可以得到二阶方程\[ \frac{\partial^2u}{\partial t^2} + \mathcal{A}u=0, \tag{7}\]其中, \(\mathcal{A}=\mathcal{B}\mathcal{B}^*\).

1. 对于线性波方程 (4)(5), 我们可以写成具有 (6)(7) 形式的抽象算子方程: \[ \begin{cases} u=P\in \mathbb{R},\ v=\mathbf{v}\in \mathbb{R}^3,\\ \mathcal{B}=c^2 \rho_0 \nabla\cdot ,\ \mathcal{B}^*=-\rho^{-1}\nabla ,\\ \mathcal{A}=- c^2 \rho_0 \nabla\cdot \left( \rho_0^{-1}\nabla \right). \end{cases}\](其中, \(\mathbf{v}\) 替换为 \(-\mathbf{v}\)).
2. 对于 Maxwell 方程, 可以写成\[ \begin{cases} u=\mathbf{E}\in \mathbb{R}^3,\ v=\mathbf{H}\in \mathbb{R}^3,\\ \mathcal{B}=\varepsilon^{-1} \nabla\times ,\ \mathcal{B}^*=\mu^{-1} \nabla\times ,\\ \mathcal{A}=\varepsilon^{-1} \nabla\times \left( \mu^{-1} \nabla\times \right). \end{cases}\]

在数值求解方面, 我们可以分别针对以上两种数学模型进行离散, 最典型的方法为有限差分和有限元.

参考

[1] Introduction to Acoustics.
[2] Ihlenburg, F. (1998). Finite Element Analysis of Acoustic Scattering. Springer-Verlag.
[3] 一维波方程的有限差分方法.