Runge 现象的数学解释

Runge 现象

考虑如下的 Runge 函数\[ f(x)= \frac{1}{1+25x^2}.\]Runge 发现如果利用区间 [-1,1] 上的等距节点\[ x_i= -1 + \frac{2i}{n},\quad i=0,1,2,…,n\]构造插值多项式 \(P_n(x)\), 那么它会在趋于区间端点时出现大幅震荡. 理论上可以证明插值误差会随多项式阶数的增加趋于无穷大:\[ \lim_{n\to\infty} \left( \max_{-1\leq x\leq 1}|f(x)-P_n(x)| \right)=\infty.\]这说明了, 采用等距节点构造高阶插值多项式的做法有时并不可取. 下面的动图生动地展示了所谓的 Runge 现象 – 插值多项式在区间的两个端点附近会产生震荡现象, 并且多项式次数越高振荡越明显. (Python 代码实现见附录)

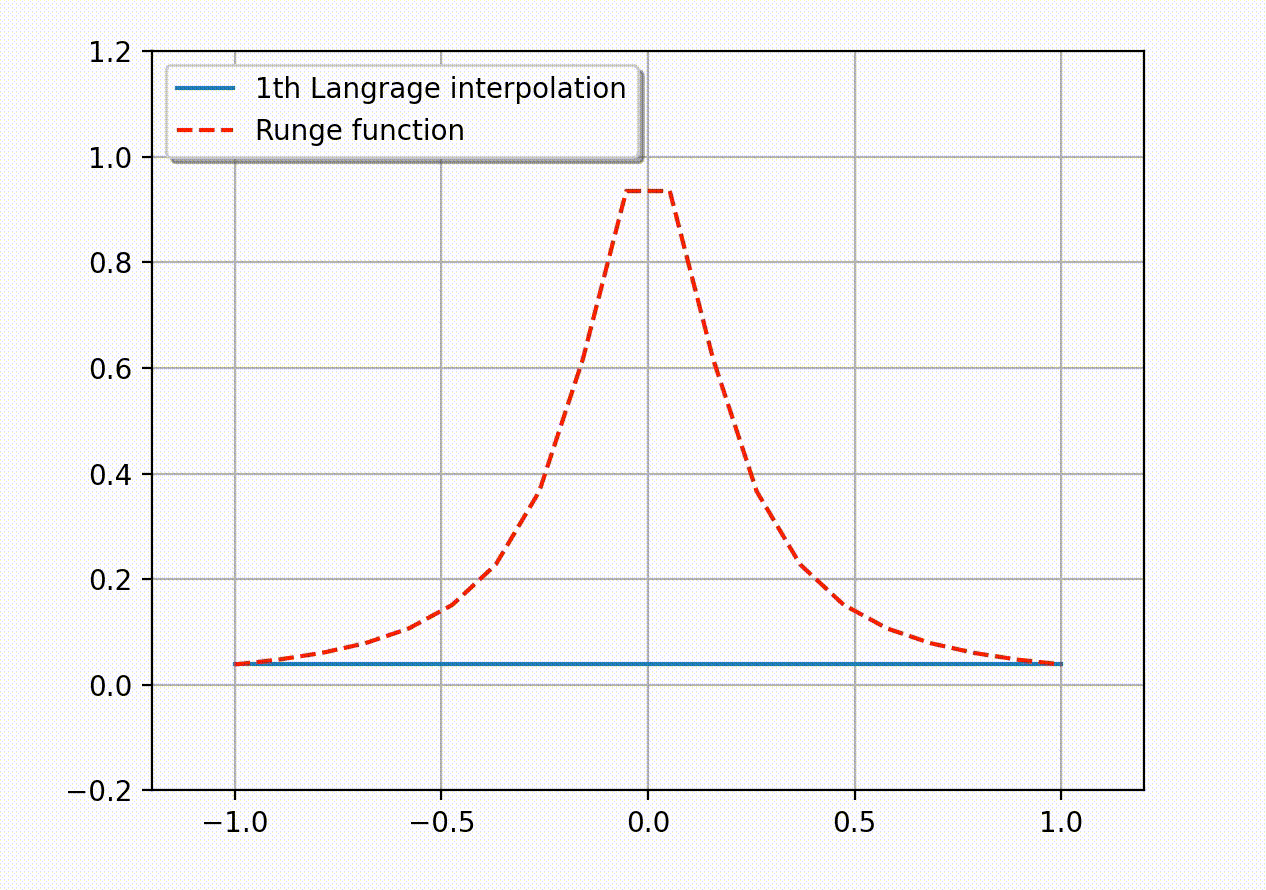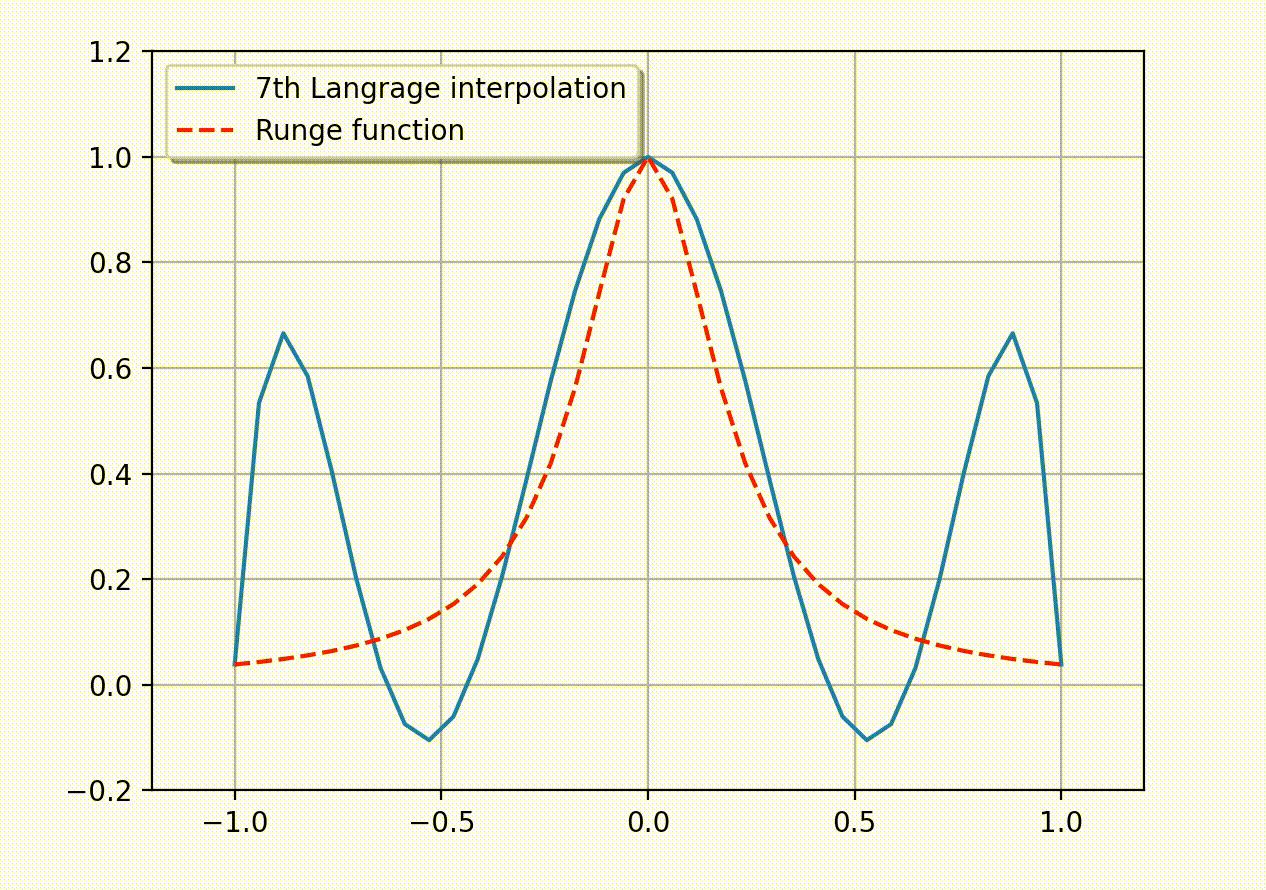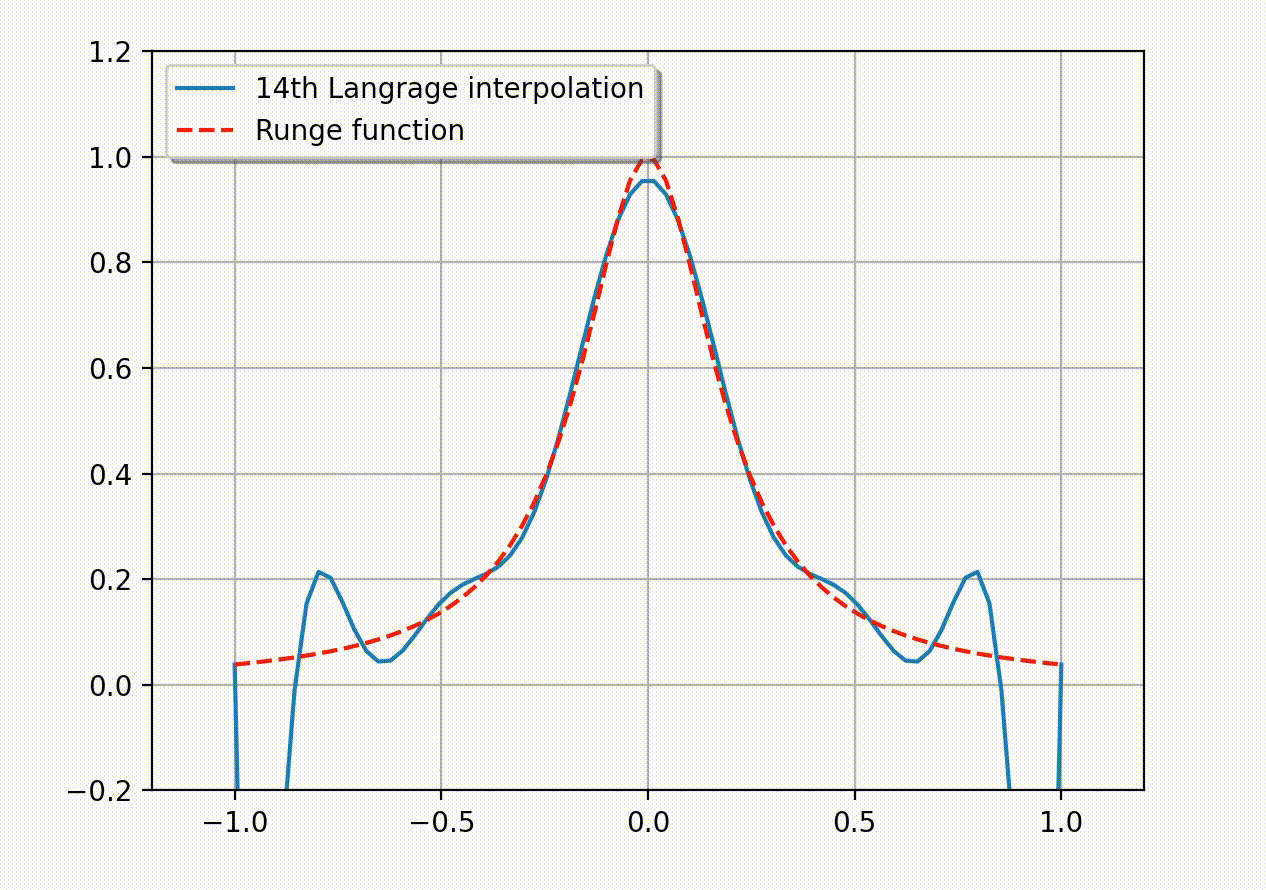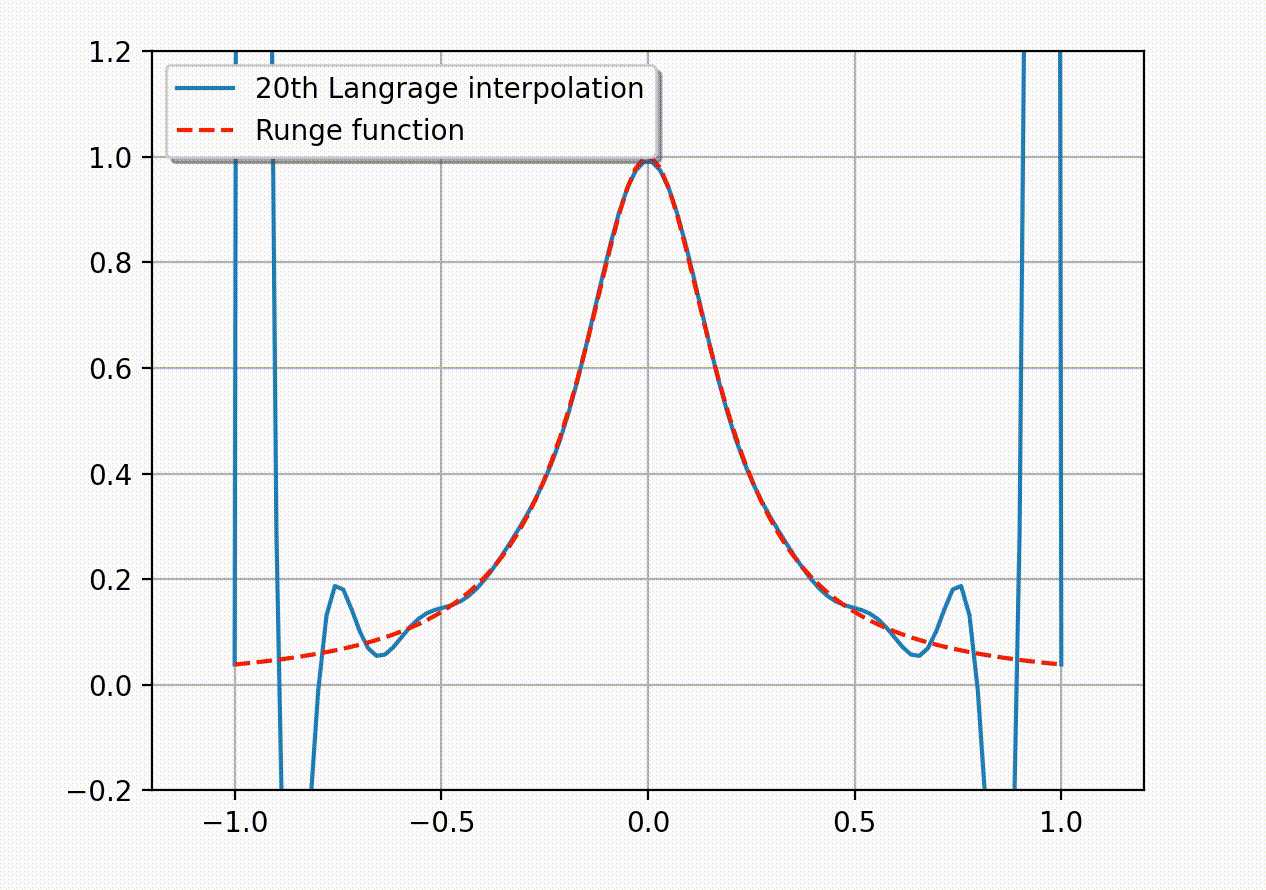
在下面的章节中, 我们将从理论上提示上述发散现象产生的原因. 在此之前, 我们有必要说明一下证明需要的数学基础:

• 关于极限的定义和基本内容
• 复变函数论中的单极点, 留数和留数定理
• 牛顿插值 (利用差商构造的插值多项式)
• Chebyshev 多项式

余项理论

定理 1 (余项估计) 令 \(f(x)\in C^n[a,b]\) 并假设 \(f^{n+1}(x)\) 在区间 \((a,b)\) 上是有定义的.\[ R_n(x):=f(x)-p_n(x) = \frac{1}{(n+1)!}\prod_{i=0}^n (x-x_i) f^{n+1}(\xi) \tag{1}\]其中, \(a<\xi< b \).

上述定理很容易在数值分析或逼近理论的教材中找到, 它提示了插值误差与被近似函数的高阶导数的关系, 是一个非常重要的结果. 但是, 一般来说, 计算一个函数的高阶导数并不容易并且找到它的极值更加困难; 另外, 这个结果很难被用来解释 Runge 现象. 所以, 我们要做的就是将这个结果推广到复平面上, 利用复变函数论中的结果来解释.

首先, 令 \(f(z)\) 为单连通区域 \(R\) 上的一个解析函数, 令 \(C\) 为区域 \(R\) 内一个简单的且可求长的闭曲线且包含互不相同的点 \(z_0,z_1,…,z_n\) 在其内部. 考虑积分\[ I = \frac{1}{2\pi i} \int_{C} \frac{f(z)}{(z-z_0)\cdots(z-z_n)} dz. \tag{2}\]这个积分中的被积函数包含多个单极点 \(z_0, z_1,…,z_n\). 因此, 由留数定理可知\[ I = \sum_{k=0}^n \frac{f(z_k)}{(z_k-z_0)\cdots(z_k-z_{k-1})(z_k-z_{k+1})\cdots (z_k-z_{n})}. \tag{3}\]

留数定理. 如果 \(z_0\) 是函数 \(g(z)\) 的单极点, 那么 Res\([g(z),z_0]=(z-z_0)g(z)_{|z=z_0}\). 举例来说, 令 \(g(z) = 1/[z(z^2+1)]\), 则 \(0\) 是一个单极点, 从而 Res(\(g,0\)) \(=(z-0)g(z)_{|z=0}=1\).

利用牛顿插值公式 (B.3) (见附录) 和 (3), 可以知道\[ I = f[z_0, z_1,\cdots, z_n ]. \tag{4}\]利用相同的理论可知\[ f[z, z_0, z_1,\cdots, z_n ] = \frac{1}{2\pi i} \int_{C} \frac{f(t)}{(t-z)(t-z_0)\cdots(t-z_n)} dt.\]因此, 通过定义 \(w_n(z) :=(t-z)(t-z_0)\cdots(t-z_n) \) 并利用牛顿插值公式可知\[\begin{align*} f(z)-p_n(z) &= f[z, z_0, z_1,\cdots, z_n ] w_n(z)\\ &=\frac{1}{2\pi i} \int_{C} \frac{w_n(z)f(t)}{w_n(t)(t-z)} dt\end{align*} \tag{5}\]

注 1. 余项公式 (5) 可以推广到多个闭曲线的情形 (即为了去掉极点): 令 \(C=\bigcup_{k=0}^M C_k\), 其中 \(C_0\) 包含所有其它的曲线, 假设 \(f\) 在 \(C_0\setminus (\bigcup_{k=1}^M C_k)\) 包含的区域上是解析的.

注 2. 若 \(f\) 在 \(z_0\) 处解析, 那么\[ \lim_{z_i\to z_0, i=1,…,n} f[z_0, z_1,\cdots, z_n ] =\frac{1}{n!}f^{n}(z_0).\]事实上, 这个结果是显然的, 因为如果利用积分 \(I\) 的定义就有\[ \frac{1}{2\pi i}\int_{C}\frac{f(z)}{(z-z_0)^{n+1}}dz = \frac{1}{n!}f^{n}(z_0).\]

复平面上的余项定理

如果插值结点全部包含在复平面上的一个有界区域内并且被插值函数在充分大的区域上是解析的, 那么我们就可以得到子区域上的一致收敛性结果. 这个结果表达了复平面上的误差与线积分的关系, 在误差分析中具有很实际的作用.

定理 2. (收敛定理) 令 \(R, S\), 和 \(T\) 有界的单连通区域, \(R\subset S\subset T\), 它们的边界分别为 \(C_R, C_S\) and \(C_T\). \(C_T\) 是一个可求长的闭曲线, 且 \(C_S\) 和 \(C_T\) 互不相交. 另 \(\delta=\text{dist}(C_T,C_R), \Delta=\max \text{dist}(C_S,C_R)\), 并且假设 \(\Delta/\delta<1\). 令插值点 \(z_i\) 包含在 \(R\) 中, \(f(z)\) 在 \(C_T\) 内解析. 那么 \(p_n(f; z)\) 在 \(S\) 上一致收敛到 \(f\).

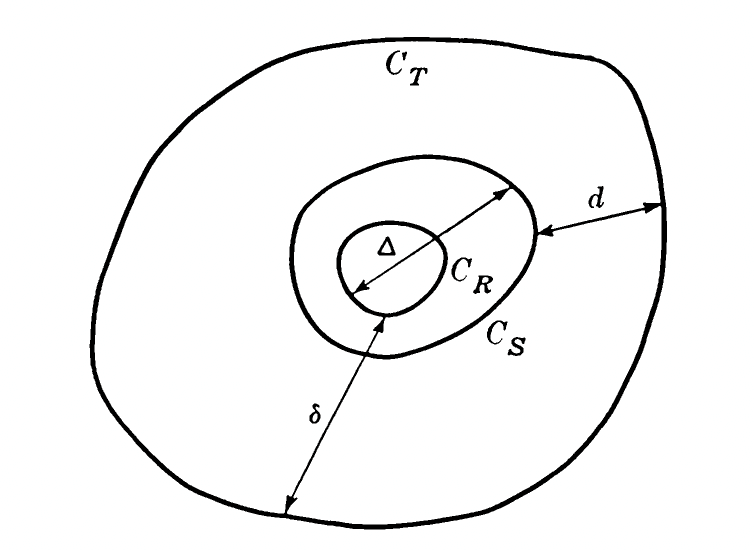
证明. 余项公式 (5) 表明\[\begin{align*} R_n(z) &= \frac{1}{2\pi i} \int_{C_T} \frac{w_n(z)f(t)}{w_n(t)(t-z)} dt\\ &\leq \frac{1}{2\pi} \int_{C_T} |\frac{|w_n(z)||f(t)|}{|w_n(t)||(t-z)|} dt\\ &\leq \frac{\Delta^{n+1}}{\delta^{n+1}} \frac{M}{d} \frac{\text{Length}(C_T)}{2\pi}\end{align*} \tag{6}\]其中 \(M=\max_{t\in C_T}|f(t)|\), \(d=\min_{t\in C_T,z\in S}\). 因此, 当 \(n\to \infty \) 时 \(R_n(z)\to 0\); 利用假设 \(\Delta/\delta<1\). \(\heartsuit\)

如果我们再次查看公式 (6) 就会注意到\[ |w_n(z)|^{1/{n+1}}\]的渐近性态包含了关于收敛的重要信息. 因此后面的分析中我们将基于如下假设: 当 \(z\) 属于复平面中的某个集合 (实际上我们将用到的是闭曲线) 上如下极限存在\[ \lim_{n \to \infty} |w_n(z)|^{1/(n+1)} = \sigma(z). \tag{7}\]请记住 \(\sigma(z)\) 这个符号, 我们将多次提到它. 上面的假设 (7) 并不是我们随意做的, 因为它在许多情况下都是成立的, 下面是两个重要的例子.

例 1. 区间 \([-1,1]\) 上等距分布的插值点 \(z_i=-1 + \frac{2i}{n}\) 满足 (7). 事实上,\[ |w_n(z)|^{1/(n+1)}=\left( \prod_{k=0}^n \left| z+1-\frac{2k}{n} \right| \right)^{1/(n+1)},\]对等式两边同时取对数可得\[ \log |w_n(z)|^{1/(n+1)} = \frac{1}{n+1} \sum_{k=0}^n \log \left| z+1-\frac{2k}{n} \right|\]由 (黎曼) 积分的定义可知 (第二个等式中使用了变量替换 \(u=-1+2t\))\[ \lim_{n \to \infty} \log |w_n(z)|^{1/(n+1)} =\int_{0}^1 \log \left| z+1-2t \right| dt =\frac{1}{2} \int_{-1}^1 \log \left| z-u \right| du \]从而, 我们就得到了 \[ \sigma(z)=\exp \left( \frac{1}{2} \int_{-1}^1 \log \left| z-u \right| du \right),\quad \forall z\in \mathbb{C}. \tag{8}\]注意, 这里 \(\sigma(z)\) 连续函数 \(|z-t|\) 的几何平均; 这个结果并不奇怪, 因为离散情形就是插值点的几何平均. \(\heartsuit\)

例 2. 令 \(z_i=\cos \left[ \left( j+\frac{1}{2} \right) \frac{\pi}{n+1} \right]\) 为 Chebyshev 节点, 即, \((n+1)\)-阶 Chebyshev 多项式的根. 那么首一多项式 \(\tilde{T}_{n+1}=w_n(t)\). 令 \(z=\rho e^{i \theta}\) 为半径为 \(\rho>1\) 的圆上的点, \(w=\frac{1}{2}(z+z^{-1})\) 就是椭圆 \(\mathcal{E}_\rho\)上的点 (它的定义参考附录 B). 从而, 下面的结果成立\[ T_n(w) = \frac{1}{2} \left( \rho^ne^{in\theta}+\rho^{-n}e^{-in\theta} \right)\]这个结果可以用归纳法证明, 这里就略了. 上面的结果表明 (利用复数的模)\[ |T_n(w)| = \frac{1}{2} \left( \rho^{2n}+2 \cos (2n\theta)+\rho^{-2n} \right)^{1/2}.\]由 Chebyshev 多项式和其首一多项式的关系 \(\tilde{T}_n = \frac{1}{2^{n-1}}T_n\), 可知对任意 \(z\in \mathcal{E}_\rho\)\[ \sigma(z)=\lim_{n \to \infty} |\tilde{T}_{n+1}(z)|^{1/n} = \lim_{n \to \infty} \frac{1}{2^{(n-1)/n}}|T_{n+1}(z)|^{1/n} =\rho/2.\tag{9}\]\(\heartsuit\)

Runge 现象的数学解释

本节中我们假设插值点为等距节点, 并且 \(\sigma(z)\) 为上一节中例 1 中的定义. 对任意 \(\rho>0\), 考虑如下一族曲线\[ C_\rho = \left\{ z\in \mathbb{C}| \sigma(z)=\rho \right\}.\]由例 1 可以得到一个显然的结果: 对 \([-1,1]\) 上的等距插值节点, 对任意 \(z\in C_\rho\)\[ |w_n(z)|^{1/(n+1)}= \left| \prod_{i=0}^n (z-z_k) \right|^{1/(n+1)} \to \sigma(z)=\rho\quad \text{as }n\to \infty .\]所以, 当 \(t\in C(\rho)\) 和 \(z\in C(\rho’),\rho'<\rho\) 时\[ \lim_{n \to \infty} \left| \frac{w_n(z)}{w_n(t)} \right| =\lim_{n \to \infty} \left( \frac{\rho’}{\rho} \right)^{n+1}=0.\]

解析的情况

当插值区间足够小时, 如 \([-.3, .3]\), 我们只需要选取一个最小的回路 \(C_\rho\) 来包含所有的插值点, 并且函数 \(f\) 在 \(C_\rho\) 围成的复平面区域内是解析的, 我们就可以得到一个复平面内的一致收敛结果. 也就是说, 如果现在我们重新回到余项公式 (5) 就容易得到如下收敛结果.

定理 3 (一致收敛) 令插值节点 \(\{z_j\}\) (Runge 现象中为等距节点) 包含在回路曲线 \(C_\rho\) 内并且假设 \(f\) 在 \(C_\rho\) 围成的区域上是解析的. 那么 \(p_n\to f\) 在 \(C_{\rho’}, \rho'<\rho\) 上是一致收敛的.
证明. 令 \(z\) 在 \(C_{\rho’}\) 内, 那么余项 (5) 表明\[ |f(z)-p_n(z)|\leq C \max_{t\in C_\rho} \left| \frac{w_n(z)}{w_n(t)} \right|\to 0.\]注意, 我们在估计中利用了函数 \(f\) 的解析性质.

包含极点的情况

如果插值区间过大, 等距插值就要求我们选取足够大的 \(C_\rho\) 来包含所有的节点, 但是同时也可能包含了函数 \(f\) 的极点 (即不是解析的). 例如 Runge 现象中的插值区间为 \([-1,1]\), 如果我们用回路 \(C_\rho\) 包含区间 \([-1,1]\), 那么它也包含了极点 \(\pm i/5\), 即 \(f\) 在 \(C_\rho\) 内不是解析的.

对于这种情况, 我们假设 \(f\) 有一个单极点 \(z^* \in C_\rho\). 那么余项公式 (5) 中的积分回路 \(C\) 应该由两部分构成: \(C_\rho\) 和一个很小的包含 \(z^*\) 的回路 (圆) \(C^*\). 因此, 如下的余项成立\[\begin{align*} f(z)-p_n(z) &= \frac{1}{2\pi i} \int_{C} \frac{w_n(z)f(t)}{w_n(t)(t-z)} dt \\ &= \frac{1}{2\pi i} \int_{C_\rho} \frac{w_n(z)f(t)}{w_n(t)(t-z)} dt + \frac{1}{2\pi i} \int_{C^*} \frac{w_n(z)f(t)}{w_n(t)(t-z)} dt\end{align*}\]其中, 第一个积分可以用上一节的方法证明当 \(n\to \infty\) 时是趋于零的. 但是问题就出在第二个积分. 因为 \(z\) 包含在 \(C_\rho\) 中, 存在 \(\rho'<\rho\) 使得 \(z\in C_{\rho’}\); 同时因为 \(z^{*}\) 在回路 \(C_\rho\) 包含的区域内, 存在某个 \(\rho^{*}<\rho\) 使得 \(z^{*}\in C_{\rho^{*}}\), 其中 \(\rho^{*}<\rho’\). 当 \(z\) 充分趋于区间端点时, 就会出现 \(\rho’ > \rho^*\) 并且 \(C^*\subset C_{\rho’}\). 下面的图给出了一个直观的理解 (左为解析, 右为非解析). 那么, 由前面的分析, 第二个积分可以写为

\[ \frac{1}{2\pi i} \int_{C^{*}} \frac{w_n(z)f(t)}{w_n(t)(t-z)} dt = \left| \frac{w_n(z)}{w_n(z^{*})} \right|\cdot \left[ \frac{(t-z^{*})f(t)}{|t-z|} \right]_{|t=z^{*}} \to C \left( \frac{\rho’}{\rho^*} \right)^n = \infty.\]综合两个积分的渐近性质, 我们得到当 \(z\) 足够接近区间端点时 \(f(z)-p_n(z)\to \infty \).

值得注意的是, 利用同样的方法, 可以证明当 \(z\) 在实轴上远离区间端点时, 我们依旧可以得到收敛的结果. 最终, 我们得到了 Runge 现象中发散的一个充分证明.

最后的讨论

目前为止, 好像所有的问题都解决了. 但是, 还有一个问题大家可能会好奇:

对于 Runge 函数 \(f(x)=1/(1+25x^2)\) 来说在多大的区间上做等距节点插值是收敛的呢?

一个充分条件是, 如果一个区间使得最小的回路 \(C_\rho\) 包含它但是不包含 \(f\) 的极点 \(\pm i/5\), 那么在这个区间上插值是一致收敛的. 利用 (8), 一个简单的计算 (可以利用符号计算) 表明\[ \sigma(\pm i/5) = 0.493758133478637\]如果代入 \(x_c=0.72667686048\) 可得 \(\sigma(x_c)=0.493758133479698\), 即 \(x_c\) 和 \(\pm i/5\) 几乎在同一条回路 \(C_{0.493758133478637}\) 上. 所以, 如果我们选取的区间包含在 \([-x_c,x_c]\) 内, 就存在一个回路 \(C_{\rho}\) 包含所有的插值点但不包含函数的极点, 由定理 3 可知插值多项式一致收敛, 从而避免 Runge 现象. 相反地, 如是区间过大, 如 \([-1,1]\) 就会出现 Runge 现象.

Chebyshev 节点插值

减小插值区间是一个避免 Runge 现象的方法, 但是实际情况是我们不能随意改变问题本身, 而是需要改变方法. 所以, 一个方法是采用 Chebyshev 节点进行插值. 以 Runge 函数主例, 我们依旧在区间 \([-1,1]\) 上进行插值, 不同的是采用 Chebyshev 节点.

可以证明在这种情况下, 完全不存在 Runge 现象. 理论证明非常简单, 这时利用例 2 的结果, \(\sigma(z)=\rho/2,\ \forall z\in \mathcal{E}_\rho\), 其中回路 \(\mathcal{E}_\rho\) 是一个以 \(\pm 1\) 为焦点的椭圆 (见附录), 并且可以任意“扁”, 即长轴相对固定, 短轴任意短. 从而, 我们可以选取充分扁 (\(\rho>0\) 充分小) 的 \(C_\rho\) 使得 \(f\) 是解析的, 然后利用定理 2 就能说明一致收敛了. 下图分别展示了 10, 20 阶插值多项式的函数图像, 并没有出现 Runge 现象.

附录

A. Python 程序

Runge 现象的代码实现

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import lagrange

def runge(x):
    return 1/(1+25*x*x)

a,b = -1, 1 # interval
n = 20      # polynomial degree
# generate interpolation data
x = np.linspace(a,b,n, endpoint=True)
y = runge(x)

# data only for plot
t = np.linspace(a,b,5*n, endpoint=True)
runget = runge(t)

Pn = lagrange(x,y)
Pnt = Pn(t)

plt.grid(True)
plt.plot(t, Pnt,'-', label=str(n)+"th Langrage interpolation")
plt.plot(t, runget,'--r', label="Runge function")
plt.legend(loc="upper left", shadow=True)
plt.axis([-1.2, 1.2, -.2,1.2])
plt.show()

\(\sigma(z)\) 的计算

from sympy import symbols, log, Abs, exp
u = symbols('u', real=True)
z = symbols('z')
# z = 1j/5          # sigma(z)=0.493758133478637
z = 0.72667686048   # sigma(z)=0.493758133479698
exp( integrate(log(Abs(z-u)), (u,-1,1)) /2)

B. Newton 插值

令 \(z_0,z_1,…,z_n\) 为 \(n+1\) 个不重合的点, 那么就有如下线性无关的 Newton 多项式\[ 1, z-z_0, (z-z_0)(z-z_1),…, (z-z_0)(z-z_1)\cdots(z-z_{n-1}).\]给定函数值 \(f(z_i),i=0,1,…,n\) 存在唯一的多项式 \(p_n(z_i)=f(z_i)\):\[ p_n(z) = a_0+a_1(z-z_0)+\ldots +a_n (z-z_0)(z-z_1)\cdots(z-z_{n-1}). \tag{B.1}\]如果分别令 \(z=z_0, …, z_n\), 我们可以求得系数 \(a_i\)\[\begin{align*} a_0 & = f[z_0] = f(z_0) \\ a_1 & = f[z_0, z_1] = \frac{f(z_1)-f(z_0)}{z_1-z_0} \\ a_2 & = f[z_0, z_1,z_2]= \frac{1}{z_2-z_0}\left( \frac{f(z_2)-f(z_1)}{z_2-z_1} – \frac{f(z_1)-f(z_0)}{z_1-z_0} \right) \\ \cdots \\ a_n & = f[z_0, z_1, \cdots, z_k ] \\\end{align*}\]其中的差商定义如下\[ f[z_0, z_1,\cdots, z_k ] = \frac{f[z_1,\cdots, z_k]-f[z_0,\cdots, z_{k-1}]}{z_k-z_0}.\]利用归纳法可以证明下面的差商的另一种形式\[ f[z_0, z_1,\cdots, z_n ] = \sum_{k=0}^n \frac{f(z_k)}{(z_k-z_0)\cdots(z_k-z_{k-1})(z_k-z_{k+1})\cdots (z_k-z_{n})} \tag{B.2}\]如果我们增加一个插值点 \(z, f(z)\), 利用相同的方法, 新的插值多项式满足\[ f(z) = p_{n+1}(z) = p_n(z) + f[z, z_0, z_1,\cdots, z_n ] (z-z_0)(z-z_1)\cdots(z-z_{n}),\]等价地, 下面的等式成立\[ f(z)-p_n(z) = f[z, z_0, z_1,\cdots, z_n ] (z-z_0)(z-z_1)\cdots(z-z_{n}),\quad \forall z\in [a,b]. \tag{B.3}\]

C. 一个共形 (conformal) 映射

下面的式子定义了复平面上的一个映射 \(z:\to w\) (参考 [2])\[ w=\frac{1}{2}(z+z^{-1}).\tag{C.1}\]令 \(w=u+iv\) 和 \(z=\rho e^{i \theta}\). 单位圆的外部, \(|z|>1\), 就被映射到 \(w\)-平面 (区间 \([-1,1]\)). 复平面上的一个点 \(\rho\cos\theta, \rho \sin \theta)\) 的像为\[ (\frac{1}{2}(\rho+\rho^{-1})\cos \theta, \frac{1}{2}(\rho-\rho^{-1})\sin \theta)\]任意圆 \(|z|=\rho>1\) 就映射为如下的椭圆\[ u = \frac{1}{2}(\rho+\rho^{-1})\cos \theta, \quad v= \frac{1}{2}(\rho-\rho^{-1})\sin \theta, \quad 0\leq \theta\leq 2\pi. \tag{C.2}\]

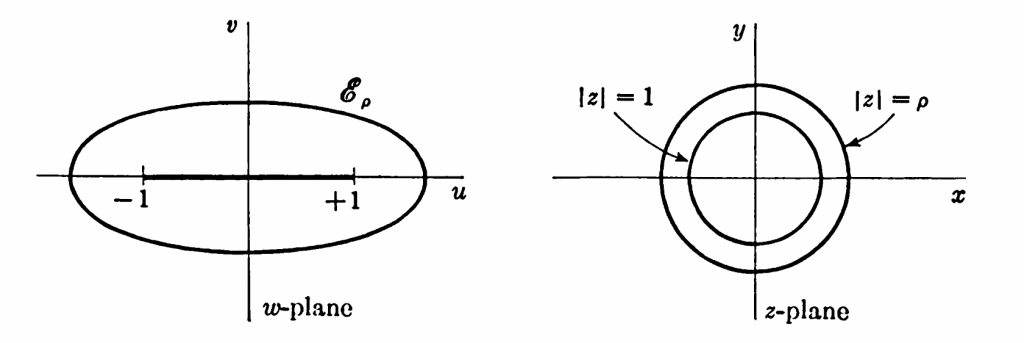
我们定义 \(\mathcal{E}_\rho\) 为以 \(\rho\) 为半径的圆的像. \(\mathcal{E}_\rho\) 的两个半轴分别是\[ a=\frac{1}{2}(\rho+\rho^{-1}),\quad b= \frac{1}{2}(\rho-\rho^{-1}),\tag{C.3}\]并且 \(a+b=\rho.\), 焦点为 \(\pm 1\).

参考

[1] J. Epperson (1987). On the Runge example. The American Mathematical Monthly. 94(4), 329-341.
[2] Phillip J. Davis (1975). Interpolation and Approximation. Dover, New York.
[3] 数值分析中的数学家 – 龙格(C. Runge)