极坐标下平面图形的面积
极坐标曲线
直角坐标系下, 平面图形中的点 \(P(x,y)\) 由两个数值确定. 对应地, 这个点在极坐标系下可以由两个数值确定 \((\rho,\theta)\), 其中 \(\rho\) 表示该点到原点 \(O\) 的距离, \(\theta\) 代表线段 \(OP\) 与 \(x\) 轴之间的夹角. 两者之间有如下的对应关系\[ \begin{cases} \rho=\sqrt{x^2+y^2},\\ \theta = \begin{cases} \arctan \frac{y}{x}\,(x >0 )\\ \left( \arctan \frac{y}{x} \right) + \pi\,(x < 0,y>0 )\\ \left( \arctan \frac{y}{x} \right) – \pi\,(x < 0,y<0 )\\ \end{cases}. \end{cases}\quad \text{and}\quad \begin{cases} x=\rho \cos \theta,\\ y=\rho \sin \theta. \end{cases}\]这样定义的变换使得 \(\theta \in [-\pi,\pi]\). 当然也可以取值 \(\theta \in [0,2 \pi]\), 这样的话, 关于 \(\theta\) 的方程需要适当变化.
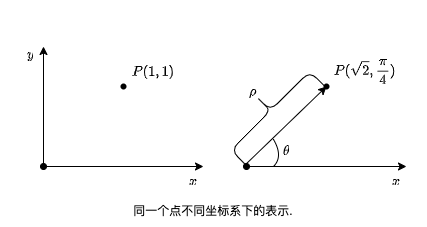
比较典型的极坐标曲线如下:
- 双纽线: \(\rho^2=a^2 \cos 2 \theta\,(a>0)\), 其中, \(\theta \in \left[ -\frac{\pi}{4},\frac{\pi}{4} \right]\cup \left[ \frac{3 \pi}{4},\frac{5 \pi}{4} \right].\)
- 螺旋线: \(\rho=a \theta\,(a>0)\), 其中, \(\theta \in \left[ 0,+\infty \right].\)
- 心形线: \(\rho=a (1+\cos \theta)\,(a>0)\), 其中, \(\theta \in [ 0,2 \pi].\)
双纽线围成的面积
由几何对称性可知, 只需计算双纽线在第一象限围成的面积. 由微元法可知, 面积微元为\[ dA = \frac{1}{2} \rho^2 \,\mathrm{d}\theta,\]这里 \(\frac{1}{2} \rho^2 \,\mathrm{d}\theta\) 是以 \(\rho\) 为半径以 \(d \theta\) 为圆心角的扇形的面积. 因此, 总的面积为\[ A = 4 \cdot \frac{1}{2} \int_{0}^{\pi/4} \rho^2 \,\mathrm{d}\theta = 4 \cdot \frac{1}{2} \int_{0}^{\pi/4} a^2 \cos 2 \theta \,\mathrm{d}\theta =a^2 \sin 2 \theta \bigg|_0^{\pi/4}=a^2.\]
现在我们简单了解一下第二个方法: 转换成直角坐标计算面积. 双纽线在直角坐标下的参数方程为\[ \begin{cases} x &= \rho \cos \theta=a \sqrt{\cos 2 \theta} \cos \theta,\\ y &= \rho \sin \theta=a \sqrt{\cos 2 \theta} \sin \theta. \end{cases}\]由微元法可知, 面积微元为\[ dA = y \,\mathrm{d}x ,\]因此, 总的面积为\[ \begin{align*} A &= 4 \int_{0}^{a} y \,\mathrm{d}x \\ &= 4 \int_{\pi/4}^{0} a \sqrt{\cos 2 \theta} \sin \theta \,\mathrm{d}(a \sqrt{\cos 2 \theta} \cos \theta) \\ &= 4 a^2 \int_{\pi/4}^{0} \sqrt{\cos 2 \theta} \sin \theta \left( \frac{1}{2}\frac{-2 \sin 2 \theta}{\sqrt{\cos 2 \theta}}\cos \theta+ \sqrt{\cos 2 \theta}(-\sin \theta)\right)\,\mathrm{d} \theta \\ &= 4 a^2 \int_{0}^{\pi/4} \sqrt{\cos 2 \theta} \sin \theta \left( \frac{ \sin 2 \theta}{\sqrt{\cos 2 \theta}}\cos \theta+ \sqrt{\cos 2 \theta}\sin \theta \right)\,\mathrm{d} \theta \\ &= 4 a^2 \int_{0}^{\pi/4} \left( \frac{1}{2}\sin ^2 2\theta + \cos 2 \theta \sin^2 \theta \right)\,\mathrm{d} \theta \\ &= 4 a^2 \int_{0}^{\pi/4} \left( \frac{1}{2}(1-\cos ^2 2\theta) + \frac{1}{2}\cos 2 \theta \cdot (1-\cos 2 \theta) \right)\,\mathrm{d} \theta \\ &= 4 a^2 \int_{0}^{\pi/4} \left( \frac{1}{2} + \frac{1}{2}\cos 2 \theta – \cos^2 2 \theta \right)\,\mathrm{d} \theta \\ &= 4 a^2 \int_{0}^{\pi/4} \left( \frac{1}{2} + \frac{1}{2}\cos 2 \theta – \frac{1}{2}(1+\cos 4 \theta) \right)\,\mathrm{d} \theta \\ &= 4 a^2 \int_{0}^{\pi/4} \left( \frac{1}{2}\cos 2 \theta – \frac{1}{2}\cos 4 \theta \right)\,\mathrm{d} \theta \\ &= 4 a^2 \left( \frac{1}{4}\sin 2 \theta – \frac{1}{8}\sin 4 \theta \right) \bigg|_{0}^{\pi/4} = a^2. \end{align*}\]