数值分析中的数学家 – 拉格朗日 (Joseph-Louis Lagrange)

简介

约瑟夫·路易斯·拉格朗日 (Joseph-Louis Lagrange)
出生: 1736 年 1 月 25 日, 意大利都灵
去世: 1813 年 4 月 10 日, 法国巴黎

拉格朗日在数学与物理领域做出了重要贡献. 做为世界上最伟大的数学家之一, 他的著作《分析力学》 (Mécanique Analytique), 通过以一种无需借助图表即可通过代数操作的形式表达运动定律, 将力学从几何学中解放出来. 拉格朗日还因发明了变分法（calculus of variations）而受到赞誉, 变分法的应用成就了一些他最重要的数学发现.

数值分析中的 Lagrange

Lagrange 插值

虽然该方法是以 Lagrange 的名字命名的, 他于 1795 年发表了该方法, 但它是由爱德华·华林 (Edward Waring) 在 1779 年首次发现的, 同时也是 1783 年莱昂哈德·欧拉 (Euler) 发表的一个公式的简单推论. Lagrange 的工作对后来的数学家产生了非常重要的影响.

给定 \(n+1\) 个离散的插值点数据\[ (x_0,y_0), (x_1,y_1), \ldots, (x_n,y_n),\]定义 Lagrange 多项式如下\[ P_n(x)=\sum_{k=0}^n y_k L_k(x), \quad L_k(x) = \prod_{i=0,i\neq k}^{n}\frac{x-x_i}{x_k-x_i},\]其中 \(L_k(x)=\begin{cases} 1 & x=x_k \\ 0 & x=x_j, j\neq k\end{cases}\) 通常称为基多项式. 可以看出, Lagrange多项式精确满足插值点数据: \(y_j=P_n(x_j)\).

高阶 Lagrange 插值多项式通常具有龙格 (Runge) 现象, 这种现象带来的高震荡问题会极大影响插值精度. 另外, 当改变某个插值点 \(x_j\) 时需要重新计算整个多项式, 所以使用牛顿插值更加方便.

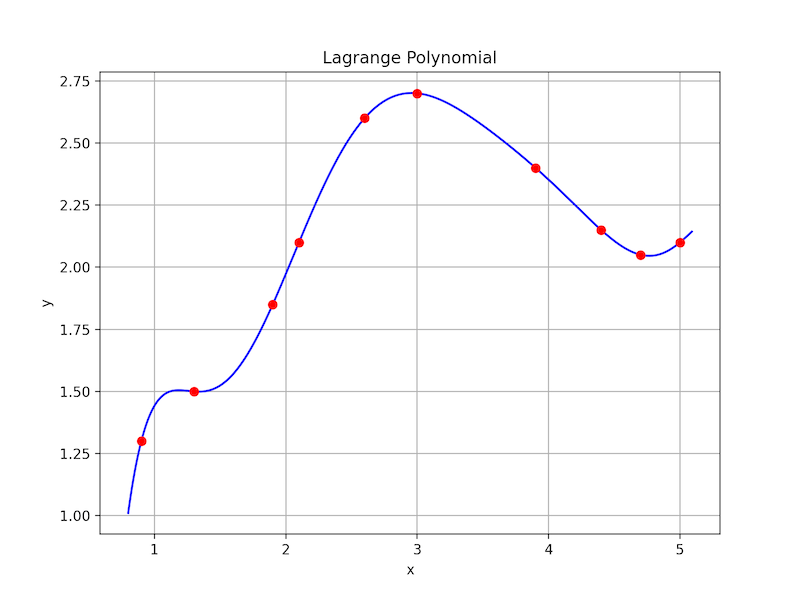
例 1. Python 中使用 Lagrange 多项式.

from scipy.interpolate import lagrange
import numpy as np
from matplotlib import pyplot as plt

x= [0.9, 1.3, 1.9, 2.1, 2.6, 3.0, 3.9, 4.4, 4.7, 5.0]
y = [1.3, 1.5, 1.85, 2.1, 2.6, 2.7, 2.4, 2.15, 2.05, 2.1]
L = lagrange(x, y)

fig = plt.figure(figsize = (8,6))
x_new = np.arange(0.8, 5.1, .01)
plt.plot(x_new, L(x_new), 'b', x, y, 'ro')
plt.title('Lagrange Polynomial')
plt.grid()
plt.xlabel('x')
plt.ylabel('y')
plt.show()

其它

Lagrange 也研究了部分正交多项式集, 但是 Chebyshev 是第一个发现其重要性的人, 并用于最小二乘逼近和概率论的研究中.

传记

早年

拉格朗日是法国和意大利的后裔, 在都灵出生5天后受洗为朱塞佩·洛德维科·拉格朗日亚(Giuseppe Lodovico Lagrangia, 1944年Sarton). 他是朱塞佩·弗朗西斯科·洛德维科·拉格朗日(Giuseppe Francesco Lodovico Lagrange)和玛丽亚·特蕾莎·格罗斯(Maria Theresa Gros) 的 11 个孩子之一 (其中只有两个活到成年). 拉格朗日负责管理撒丁岛王国的军事金库, 玛丽亚·特蕾莎·格罗斯是一位富有的医生的独生女. 拉格朗日的父亲有良好的社会地位和财富, 但在他的儿子长大之前, 他已经在投机中失去了大部分财产, 年轻的拉格朗日不得不依靠自己的能力来获得他的地位.

他在都灵学院 (College of Turin) 接受教育, 在那里他第一次接触到以哲学为主题的数学研究. 最初, 他对这门学科没什么兴趣, 但第二年又必须回到同一个班级 (复读), 并花费更多精力来应对这门学科. 埃德蒙·哈雷 (Edmund Halley) 倾向于利用代数而非几何做为分析的工具, 他的一篇论文极大地激发了拉格朗日对数学的兴趣. 在拉格朗日十七岁的时候, 他全身心地投入到数学研究中, 很快就精通这个领域. 十九岁时, 他被任命为皇家艺术学院（Royal School of Artillary）的数学讲师.

信件

拉格朗日在这里工作的第一个成果是他在 1854 年左右写给著名数学家莱昂哈德·欧拉 (Leonhard Euler), 其中他解决了半个多世纪以来一直是数学家讨论的主题的等周长问题. 促使拉格朗日写这封信的是欧拉在其回忆录中的一篇声明, 将问题的解决留给了“形而上学家”. 拉格朗日读了这篇论文, 欧拉的不同寻常的评论唤醒了他的兴趣.

等周长问题, 简单地以二维形式表示, 是找到闭合曲线的形状, 例如一个绳环, 使得在固定周长的情况下围成的面积最大. 为了解决这个问题, 拉格朗日采用了后来被欧拉命名的变分法的新领域, 尽管它被零星地应用于特定问题, 但拉格朗日却发展出了它最大的通用性.

欧拉认识到年轻的拉格朗日信中采用的方法的便利性, 以及它比他自己使用的方法的优越性. 他以特有的礼貌保留了一篇他以前写过的论文, 其中涵盖了一些相同的内容, 以便这位年轻的意大利人可能有时间完成他的工作, 并声称毫无争议地发明了新微积分. 这篇论文立刻将拉格朗日置于当时数学家的前列.

Miscellanea Taurinensia

1758 年, 在他的学生的帮助下, 拉格朗日成立了一个学会, 该学会随后被合并为都灵学院, 他的大部分早期著作都可以在它的五卷交易中找到, 通常被称为《Miscellanea Taurinensia》, 其中许多是精心制作的论文. 第一卷包含一篇关于声音传播理论的论文; 其中指出了艾萨克·牛顿 (Isaac Newton) 犯的一个错误, 获得了运动的一般方程, 并得到了直线运动的解. 本卷还包含了弦横向振动问题的完整解决方法; 在论文中, 他指出 Brook Taylor、 Jean le Rond d’Alembert 和 Euler 先前给出的解缺乏普遍性, 并得出结论: 曲线在任何时间 \(t\) 由方程给出 \(y=a\sin(mx)\cdot \sin(nt)\). 文章最后对回声、节拍和复合声音进行了巧妙的讨论. 本卷中的其他文章是关于循环序列、概率和变分法的.

第二卷包含一篇长篇论文, 其中体现了第一卷中关于变分法的理论和符号的几篇论文的结果; 他通过推导最小作用原理和解决动力学中的各种问题来说明它的用途.

第三卷包括通过变分法解决几个动力学问题; 一些关于积分的论文; 皮埃尔·德·费马 (Pierre de Fermat) 问题的解决方案, 找到一个数 \(x\) 使 \(x^2n + 1\) 成为一个平方数, 其中 \(n\) 是一个给定的整数但不是平方数; 以及在相互引力作用下运动的三个物体的一般运动方程.

健康受损

1761 年, 拉格朗日成为世界上在世的最重要的数学家, 没有之一. 但前九年的不断劳作严重影响了他的健康, 医生拒绝为他的理智或生命负责, 除非他能够休息并且锻炼. 虽然他的健康暂时恢复了, 但他的神经系统一直没有完全恢复元气, 此后他不断遭受严重的忧郁症的侵扰.

中年

他的下一部作品是 1764 年关于月球天平动的, 其中解释了为什么同一面总是转向地球, 他借助虚功原理解决了这个问题. 他的解决方案特别有趣, 因为它包含了广义运动方程概念的萌芽, 这些方程是他在 1780 年首次正式证明的.

宫廷

不久后他启程前往伦敦, 但是途中病倒在了巴黎. 在那里, 他受到了极大的荣誉, 会见了当时著名的数学家, 如达朗贝尔 (d’Alembert) 和克莱罗(Alexis Clairaut); 遗憾的是, 他离开了这座城市的辉煌社会, 回到了都灵的乡土生活. 然而, 他在皮埃蒙特省 (Piedmont) 的逗留时间很短. 1766 年欧拉离开柏林, 腓特烈大帝 (Frederick the Great) 写信给拉格朗日, 表达了“欧洲最伟大的国王”希望“欧洲最伟大的数学家”常驻他的宫廷的愿望. 同年, 他因对木星卫星运动的研究而获奖.

拉格朗日接受了腓特烈大帝的提议, 并在接下来的 20 年里在普鲁士 (Prussia), 在那里他不仅撰写了在柏林和都灵稿件中发表的长篇系列论文, 还撰写了他的不朽著作《分析力学》(Mécanique Analytique). 他在柏林的生活始于婚姻. 由于他发现他的大多数同事都结婚了, 并且他们的妻子向他们保证这是幸福的唯一途径, 他结婚了. 然而, 尽管他对她妻子–一个亲戚–非常关注, 但她因体质虚弱很快就去世了, 还有一个儿子也死了.

拉格朗日是国王的宠儿, 他经常与他谈论完美规律的生活的好处. 从那时起, 拉格朗日像研究力学一样研究他的思想和身体, 并通过试验找到了他能够在不崩溃的情况下完成的确切工作量. 每天晚上, 他都给自己明确地定下第二天的任务, 在完成某一学科的任何一个分支时, 他都会写一个简短的分析, 看看证明中的要点或与主题相关的哪些点可以改进. 他总是在开始撰写论文之前就考虑好论文的主题, 并且通常直接写下来, 没有一次擦除或更正.

分析力学 (Mécanique Analytique)

他在柏林的最重要的论文构成了他的伟大专著《分析力学》. 其中, 他提出了虚功原理, 并根据这一基本原理, 借助变分法推导出整个力学, 包括固体和流体.

拉格朗日追随了达朗贝尔的工作, 他是第一个通过虚速度原理将运动问题简化为静力学问题的人. 根据这个原理, 运动中的系统基本上会受到力的影响, 将其变成静态系统, 然后确定力和实际运动.

Mécanique Analytique 的目的展示整个学科隐含在一个单一的原理中, 并给出可以从中获得任何特定结果的通用公式. 他得到的广义坐标法也许是他分析中最出色的结果. 他不像达朗贝尔和欧拉那样, 遵循物质系统各部分的运动, 而是证明, 如果我们通过足够多的变量来确定系统的状态, 这些变量的数量与系统拥有的自由度的数量相同, 然后系统的动能和势能可以用这些变量表示, 并由此导出运动方程.

在此处给出的其他次要定理中，可能会提到这样一个命题，即在给定约束下由给定脉冲赋予材料系统的动能是最大值，并且是最小作用原理。 所有的分析都如此优雅, 以至于威廉·罗文·汉密尔顿 (William Rowan Hamilton) 说这部作品只能被描述为一首科学诗. 有趣的是，拉格朗日说力学实际上是纯数学的一个分支, 类似于四维几何, 即时间和空间点的三个坐标. 据说他为自己从工作开始到结束没有一张图表而自豪. 起初找不到出版这本书的印刷商, 但阿贝·玛丽 (Abbe Marie) 最终找到了一个书商来承销印刷, 前提是如果这本书卖不出去作者承担一半的损失. 在 1788 年印刷之前, 阿德里安·玛丽·勒让德 (Adrien-Marie Legendre) 监督了对作品的修正.

晚年

腓特烈大帝于 1787 年去世, 拉格朗日发现柏林的气候很不适宜, 欣然接受了路易十六提出的移居巴黎邀请. 他也收到了来自西班牙 (Spain) 和那不勒斯 (Naples) 的类似邀请. 在法国, 他受到了各种各样的礼遇, 卢浮宫为他准备了特殊的公寓, 他还成为了科学院的院士, 这个科学院后来成为国家研究所的一部分. 刚开始在巴黎居住时, 他就患上了忧郁症, 甚至他那本已写了四分之一个世纪的《Mécanique》的印刷版, 也已搁在他的书桌上两年多都没有打开过. 对法国大革命 (French Revolution) 结果的好奇首先把他从倦怠中唤醒，随着革命的发展, 这种好奇很快变成了警报.

大约在同一时期, 1792年, 他生活中莫名其妙的悲伤和他的胆怯感动了一个年轻女孩的同情心, 她坚持要嫁给他并证明了她是一个忠诚的妻子, 他对她产生了强烈的感情. 尽管 1793 年 10 月命令所有外国人离开法国的法令明确免除了他的名字, 但当他被任命为度量衡改革委员会 (The Commission for the Reform of Weights and Measures) 主席时, 他正准备逃跑. 委员会的最终决定在很大程度上归功于他, 1799 年委员会接受了十进制细分 (the decimal subdivision), 这主要是由于他的影响. 1795年, 拉格朗日成为经度局 (the Bureau des Longitudes) 的创始成员之一.

虽然拉格朗日已经下定决心趁机逃离法国, 但他从来没有遇到任何危险. 不同的革命政府 (以及后来的拿破仑 (Napoleon) ) 赋予他荣誉和赞赏. 一个惊人的证据证明了他受到的尊重, 在 1796 年, 法国驻意大利的代表奉命全副武装地会见拉格朗日的父亲, 并就他儿子取得的成就表示共和国的祝贺: “他的天才为全人类赢得了荣誉, 生下这样的孩子是皮埃蒙特的特殊荣耀.”

需要补充一点的是, 拿破仑上台后热心倡导在法国进行科学研究, 并且给予慷慨捐助. 拉格朗日设法避免对法国革命派别和拿破仑政府的愤怒, 因为在他之前工作期间始终远离政治, 并且在表达政治信仰时对自己有一定程度的克制. 即便如此, 在安东尼·拉瓦锡 (Antoine Lavoisier,) 被处决后他还是计划离开巴黎前往柏林, 但巴黎的事态发展令他留在了那里.

师范学院 (École Normale)

1795 年，拉格朗日被任命为新成立的高等师范学院 (École Normale Supérieure) 的数学主席, 这是一家仅存在四个月的教师培训机构. 他在这里的讲座都是很基础的, 没有什么特别重要的内容, 但这些讲座被出版了, 因为教授们必须 “向人民代表和彼此保证, 既不阅读, 也不背诵.” 这些讲座被要求用速记记录下来, 以便代表们能够看到教授们是如何表现自己的.

巴黎综合理工学院 (École Polytechnique)

1797 年，巴黎综合理工学院 (École Polytechnique) 成立, 拉格朗日成为教授. 他的讲座被有幸参加的数学家描述为在形式和内容上几乎完美无缺. 从最简单的内容开始, 他带领他的听众, 甚至他们自己也不知道, 他们自己正在开拓主题的范围. 最重要的是, 他让学生认识到以对称符号表示一般方法的优势.

他关于微积分的讲座构成了《分析理论》(Théorie des fonctions analytiques) 的基础, 该著作于 1797 年出版. 这项工作是他在 1772 年寄给柏林报纸的一篇论文中的一个想法的延伸, 用一组基于代数函数级数发展的定理来代替微分学. 在 1758 年发表于伦敦的 《残差分析》中, 约翰·兰登 (John Landen) 曾使用过类似的方法. 拉格朗日相信他可以因此摆脱那些与使用无限大和无限小量有关的困难, 而这些无穷大量和小量正是哲学家们在微分学通常处理中所反对的. 这本书分为三个部分：其中第一部分是关于函数的一般理论，并给出了泰勒定理 (Taylor’s theorem) 的代数证明, 然而其正确性是值得商榷的; 第二个涉及几何应用; 第三个是应用力学. 同一方向的另一篇论文是发表于 1804 年的 (Leçons sur le calcul des fonctions). 这些工作也许可以看作是奥古斯丁·路易斯·柯西 (Augustin Louis Cauchy)、卡尔·古斯塔夫·雅各比 (Carl Gustav Jakob Jacobi) 和卡尔·魏尔斯特拉斯 (Karl Weierstrass) 科学研究的起点.

无穷小 (Infinitesimals)

后来，拉格朗日重新使用了无穷小, 而不是把微积分建立在对代数形式的研究上; 在《分析力学》第二版的序言中, 他论证了使用无穷小是正当的, 并且总结说:

当我们掌握了无穷小方法的真谛, 并利用主要的几何方法和最终比率或者利用导函数的解析方法验证了它的结果的正确性后, 我们就可以用无穷小量作为一种确定的、有价值的工具来缩短和简化我们的证明.

行星运动

行星运动理论已经成为拉格朗日柏林论文中一些最引人注目的主题之一. 在 1806 年, 西蒙·泊松（Simeon Poisson）重新开启了这个主题, 他在法兰西学院阅读的一篇论文中表明, 拉格朗日的公式导致运动轨道稳定性存在一定的限制. 拉格朗日参与并重新讨论了整个主题, 在 1808 年给学院的一封信中解释了如何通过任意常数的变化来确定任意相互作用的物体系统的一些重要特征.

最后的岁月

1808 年, 拿破仑任命拉格朗日为荣誉军团 (Legion of Honor) 的大军官勋位和帝国伯爵 (A comte of the empire). 1810 年, 他开始对《分析力学》进行彻底的修订. 但在他去世前只完成了大约三分之二的内容. 1813 年, 他在巴黎去世前一周被授予法国留尼汪帝国大十字勋章 (the Grand Croix of the Ordre Impérial de la Réunion)

同年三月, 开始经受痉挛和昏厥的折磨. 4 月, 他与最亲密的同事进行了最后一次会面并透露他并没有将即将到来的死亡视为一件不愉快的事情. 仅仅两天后, 他就安详地离开了人世. 同年, 他被安葬在巴黎的万神殿 (Panthéon). 他坟墓上的法文铭文写道:

约瑟夫·路易斯·拉格朗日. 参议员. 帝国伯爵.
荣誉军团大军官勋位.
留尼汪帝国大十字勋章.
法兰西学会和经度局成员.
1736 年 1 月 25 日生于都灵. 1813 年 4 月 10 日卒于巴黎.
JOSEPH LOUIS LAGRANGE. Senator. Count of the Empire.
Grand Officer of the Legion of Honour.
Grand Cross of the Imperial Order of Réunion.
Member of the Institute and the Bureau of Longitude.
Born in Turin on 25 January 1736. Died in Paris on 10 April 1813.

论著

在腓特烈大帝宫廷 22 年间, 拉格朗日不仅写出了精彩的 《分析力学》, 还为都灵学院、柏林皇家学院和法兰西学院贡献了两百篇论文. 其中一些是真正的论文, 无一例外都是非常优秀的. 除了生病的那段时间, 他平均每月大约写一篇论文. 所有的成果中, 以下内容最为重要.

首先, 《分析力学》第四和第五卷的贡献 (1766-1773); 其中最重要的是 1771 年的那篇文章, 他在其中讨论了如何将众多的天文观测结合起来以得出最可能的结果. 后来，他向都灵学院提交前两卷 (1784-1785); 在第一卷中, 他发表了一篇关于运动中流体施加的压力的论文, 在第二卷中发表了一篇关于使用无穷级数解决微积分问题的文章.

大部分寄往巴黎论文都是关于天文学问题的, 其中应该特别提到他在 1766 年关于木星系统的论文, 他在 1772 年关于三体相互引力影响下的问题的论文; 他的 1773 年关于月球轨道的论文和 1778 年关于彗星轨道的论文. 这些论文都是针对法兰西学院提出的主题撰写的, 并且在每种情况下都将奖项授予了他.

1772 年至 1788 年间, 拉格朗日重新制定了经典/牛顿力学, 以简化公式并方便计算. 这些力学称为拉格朗日力学.

然而，他在此期间的大部分论文都贡献给了柏林皇家学院. 其中一些论文研究代数问题. 特别是:
1. 1770 年和 1771 年, 他关于求解任意阶代数方程的一般过程的论文; 这种方法对四阶以上的方程无效, 因为它涉及到比所提出的方程更高维的方程的解, 但它给出了已知的所有解作为对单一原理的修改.
2. 任意阶二项式方程的完全解; 这包含在最后提到的论文中.

他早期的几篇论文也涉及数论问题. 其中包括：

• 他证明了每个不是平方的正整数都可以表示为两个、三个或四个整数平方之和的定理, 1770.
• 他证明了威尔逊定理 (Wilson’s theorem), 即如果 \(n\) 是素数, 当且仅当 \((n-1)!+1\) 可以整除 \(n\) (1771 年).
• 他在 1773 年、1775 年和 1777 年的论文中论证了费马的几个以前没有得到证明的结果.
• 他是第一个证明佩尔方程 (Pell’s equation) 总有解的人.
• 最后，他提出了确定形如 \(x^{2}+ay^{2}\) 的数的因子的方法.

还有许多关于解析几何各个方向的文章. 从 1772 年到 1785 年, 他发表了一系列论文, 创造了偏微分方程科学, 该科学处理了必须考虑函数相对于两个或多个自变量的变化率的情况. 这些结果的很大一部分收集在 1794 年出版的第二版欧拉积分学中.

最后，有许多关于天文学的论文, 其中最重要的是：

• 试图解决导致拉格朗日点发现的三体问题 (1772 年).
• 关于椭球的吸引力 (1773 年): 这是建立在麦克劳林 (Maclaurin) 的工作之上的.
• 关于月球的长期方程 (1773 年), 因最早引入势能概念而引人注目. 物体在任何一点的势能是物体每个元素的质量之和除以它到该点的距离. 拉格朗日表明, 如果知道物体在外部点的势力, 则可以立即找到任何方向的吸引力. 1777 年寄往柏林的一篇论文详细阐述了势能理论.- 关于行星轨道节点的运动 (1774 年).
• 关于行星轨道的稳定性 (1776 年).- 在 1778 年和 1783 年的两篇论文中, 完全确定了通过三次观测确定彗星轨道的方法.
• 他在 1781-1784 年间对行星元素变化的确定: 得到的上限与后来勒维耶 (Le Verrier) 获得的结果非常吻合, 拉格朗日在当时所拥有的关于行星质量的知识允许的范围内继续进行.
• 三篇关于插值法的论文 (1783、1792 和 1793 年): 其中涉及的有限差分部分, 现代与过去拉格朗日离开的时代基本相同.

影响

拉格朗日将永远在最伟大的数学家中广为人知, 主要是因为他对力学科学的分析表达, 在他关于这一主题的主要著作发表后, 他不再受尴尬的几何分析的束缚. 力学中的一切都可以简化为对定义特定问题的变量的操纵.

他的分析方法具有更广泛适用性的一般原理, 替代了牛顿的方法. 18 世纪的科学家们很快意识到, 他们需要比牛顿方法提供的更强大的工具来解决力学问题, 这些工具是由 d’Alembert 提供的, 特别是拉格朗日在他的《分析力学》. 他的工作后来被其他研究人员扩展, 尤其是英国数学家威廉·罗文·汉密尔顿 (William Rowan Hamilton).

拉格朗日对变分法的发明和使用本身就成为了一个领域, 并成为了追随他的物理学家和数学家的有力工具.

参考

[1] Joseph-Louis Lagrange. New World Encyclopedia.

– Asimov, Isaac. Asimov’s Biographical Encyclopedia of Science and Technology, 2nd ed. New York: Doubleday, 1982. ISBN 0385177712
– Gillispie, Charles Coulston. Dictionary of Scientific Biography. New York: Scribner, 1975. ISBN 0684101211
– Grant, Robert. History of Physical Astronomy: From the Earliest Ages to the Middle of the Nineteenth Century. Forgotten Books, 2017. ISBN 1330281381
– Porter, Roy, and Marilyn Ogilvie (eds.). The Biographical Dictionary of Scientists, 3rd ed. New York: Oxford University Press, 2000. ISBN 0195216636
– Sarton, George. Lagrange’s Personality. Proceedings of the American Philosophical Society 88 (1944): 457.
– Thomson, Thomas (ed.). Annals of Philosophy, Or, Magazine of Chemistry, Mineralogy, Mechanics, Natural History, Agriculture and the Arts Volume 2. Nabu Press, 2010. ISBN 1147031339
– Thomson, Thomas (ed.). Annals of Philosophy, Or, Magazine of Chemistry, Mineralogy, Mechanics, Natural History, Agriculture and the Arts Volume 4. Forgotten Books, 2019. ISBN 0331344963
– Young, Thomas. Miscellaneous Works of the Late Thomas Young. HardPress Publishing, 2013. ISBN 1313016543

– ohn J. O’Connor and Edmund F. Robertson. Joseph-Louis Lagrange at the MacTutor archive
– Joseph Louis Lagrange (1736 – 1813) From A Short Account of the History of Mathematics (4th edition, 1908) by W.W. Rouse Ball.
– The Lagrange Points – WMAP Observatory (NASA)
– Joseph-Louis Lagrange Famous Scientists
– Biography of Joseph Louis Lagrange, Mathematician By Deb Russell, ThoughtCo.