一阶 Maxwell 方程的间断 (DG) 有限元方法

2022年7月22日2022年7月22日 numanal 0 个评论 DG, Maxwell方程, 间断有限元

Maxwell 方程

我们知道, 间断有限元方法 (discontinuous Galerkin, DG) 在求解 Maxwell 方程时相比与有限差分时域 (FDTD) 方法具有相当大的优势. 例如, 间断有限元方法可以使用不同形状的协调或非协调网格; 使用多种基函数; 较少的网格单元信息耦合带来更高的并行效率. 尽管如此, 我们依然需要注意经典的 FDTD 方法目前为止依然非常活跃, 最主要的原因之一便是它在程序实现方面非常简单. 在这篇文章中, 我们简要介绍一下 DG 求解一阶时间依赖的 Maxwell 方程的数值格式, 它可以很容易地推广到三维的情形.

假设 \(\Omega\in \mathbb{R}^d,d=2,3\) 是一个单连通的 Lipschitz 区域. 考虑横波 (TM) Maxwell 方程\[\begin{align*} \frac{\partial E}{\partial t} &= \nabla\times \mathbf{H}, \\ \frac{\partial \mathbf{H}}{\partial t} &= -\overrightarrow{\nabla}\times E,\end{align*} \tag{1a,b}\]初始条件为\[ E(0) = E_0(x,y),\quad \mathbf{H}(0)=\mathbf{H}_0(x,y). \tag{2}\]其中, 我们利用了二维空间中的微分算子: 向量和标量函数的旋度算子 (curl operator)\[ \nabla\times \mathbf{H} := \frac{\partial H_2}{\partial x_1} – \frac{\partial H_1}{\partial x_2}, \quad \overrightarrow{\nabla}\times E := \begin{bmatrix} \frac{\partial E}{\partial x_2}\\ -\frac{\partial E}{\partial x_1} \end{bmatrix}.\]为了表述一个完整的问题, 我们还需要赋予如下任意一个边界条件: 在 \(\partial \Omega\) 上\[ \mathbf{n}\times \mathbf{H}=g,\\ \mathbf{n}\times E = \mathbf{g}, \tag{3a,b}\]其中 \(\mathbf{n}\times \mathbf{H} := n_1H_2-n_2H_1\) 且 \(- E\times \mathbf{n} = \mathbf{n}\times E := \begin{bmatrix} n_2 \\-n_1 \end{bmatrix}E\).

半离散格式

假设 \(\mathcal{T}_h\) 是区域 \(\Omega\) 的一族网格, 通常为非重合的三角形或四边形网格. 令 \(\mathcal{F}_h\) 为所有单元面(边)的集合, \(\mathcal{F}_h^I\) 和 \(\mathcal{F}_h^B\) 分别表示内部和边界面的集合. 给定 \(F \in \mathcal{F}_h\), 其上的单位向量为 \(\mathbf{n}=[n_1,n_2]^T\), 由 \(K^-\) 指向 \(K^+\). 函数 \(v\) 的跳跃和平均定义如下\[ [\![v]\!] = v^- -v^+,\quad \left\{\! \left\{ v \right\}\! \right\}= \frac{1}{2} ( v^-+v^+).\]定义 \(N\)-阶间断有限元空间为\[ V_h:= \left\{ v\in \mathbb{P}_N(K),\ K\in \mathcal{T}_h \right\}.\]

给定边条件 (3a), Maxwell 方程 (1) 的间断有限元 (DG) 格式定义如下 [1,2]: 寻找 \(E_h\in V_h, \mathbf{H}_h\in [V_h]^2\) 满足\[ \begin{equation} \begin{split} &\int_{\Omega} \left(\frac{\partial E_h}{\partial t} -\nabla\times \mathbf{H}_h \right) V dx +\int_{\mathcal{F}_h} [\![ \mathbf{n}\times \mathbf{H}_h]\!] \left\{\! \left\{ V \right\}\! \right\} + \int_{\mathcal{F}_h^I} \frac{\alpha}{2} [\![E_h]\!] [\![V]\!] =\int_{\mathcal{F}_h^B} g V , \\ &\int_{\Omega} \left( \frac{\partial \mathbf{H}_h}{\partial t} +\nabla\times E_h \right)\cdot \mathbf{W} dx -\int_{\mathcal{F}_h^I} [\![\mathbf{n}\times E_h]\!] \cdot \left\{\! \left\{ \mathbf{W} \right\}\! \right\} +\int_{\mathcal{F}_h} \frac{\alpha}{2} [\![\mathbf{H}_h]\!]_T \cdot [\![\mathbf{W}]\!]_T =\int_{\mathcal{F}_h^B} \frac{\alpha}{2} g (\mathbf{n}\times\mathbf{W}), \end{split}\end{equation} \tag{4}\]对任意 \(V\in V_h\) 和 \(\mathbf{W}\in [V_h]^2\) 都成立. 假定 \(\alpha=1\). 其中, 我们需要注意的是离散解 \(\mathbf{H}_h\) 的切向分量定义为\[ (\mathbf{H}_h)_T := (\mathbf{n}\times \mathbf{H}_h)\times \mathbf{n} = \begin{bmatrix} – n_{2} \left(- H_{1} n_{2} + H_{2} n_{1}\right)\\n_{1} \left(- H_{1} n_{2} + H_{2} n_{1}\right) \end{bmatrix} .\]

注. 在间断有限元方法 (4) 中, 我们是以弱形式赋予边界条件 (3a) 的. 这种方法给编程实现带来极大的便利, 因为我们可以使用单项式基函数而不是 Lagrange 基函数.

全离散格式

令 \(e_h\) 为数值解 \(E_h\) 的系数向量, 那么全离散的 DG 格式定义如下:\[ \begin{align} M_e \frac{e_h^{n+1}-e_h^n}{\Delta t} &= (N_h – S_h) \mathbf{h}_h^{n+1/2} – P_e e_h^{n}+ G_e \\ M_h \frac{\mathbf{h}_h^{n+3/2}-\mathbf{h}_h^{n+1/2}}{\Delta t} &= (- N_e + S_e) e_h^{n+1} – P_h \mathbf{h}_h^{n} + G_h. \end{align} \tag{5a,b}\]其中, 令 \(\phi_j, \psi_j\) 分别为空间 \(V_h\) and \([V_h]^2\) 的基函数, 那么 (5a) 中涉及到的系数矩阵为\[ (M_e)_{ij} = \int_{\Omega} \phi_j \phi_i,\quad (N_h)_{ij} = \int_{\mathcal{F}_h} [\![\mathbf{n}\times \psi_j]\!] \left\{\! \left\{ \phi_i \right\}\! \right\},\\ (S_h)_{ij} =\int_{\mathcal{F}_h} [\![\mathbf{n}\times \psi_j]\!] \left\{\! \left\{ \phi_i \right\}\! \right\},\quad (P_e)_{ij}=\int_{\mathcal{F}_h^I} \frac{\alpha}{2} [\![\phi_j]\!] [\![\phi_i]\!], \quad (G_e)_i = \int_{\mathcal{F}_h^B} g \phi_i.\]

数值算例

例 1. 考虑单位区域 \([-1,0]\times [0,1]\) 上的 Maxwell 方程, 其它解析解设为如下的平面波\[ \begin{align*} H_1 &= a_1 \sin (\omega t+\alpha_1 x_1 + \alpha_2 x_2),\\ H_2 &= a_2 \sin (\omega t+\alpha_1 x_1 + \alpha_2 x_2),\\ E &= a_3 \sin (\omega t+\alpha_1 x_1 + \alpha_2 x_2). \end{align*}\]由方程 (1) 可知\[ a_1 \omega = – a_3 \alpha_2,\quad a_2 \omega = a_3 \alpha_1,\quad a_3 \omega = a_2 \alpha_1 – a_1 \alpha_2.\]容易证明如下的频散关系 \(\omega^2=\alpha_1^2+\alpha_2^2\). 因此, 我们可以考虑如下简单的情形: \(\omega=15, \alpha_1=\alpha_2=-\omega \cos \frac{\pi}{4}=-\frac{\omega}{\sqrt{2}} \), \(a_3=1\). 直接计算可知 \(a_1=\cos \frac{\pi}{4},\ a_2=-\cos \frac{\pi}{4}\). 这种情况下, 平面波是一个偏向 \(45^\circ \) 角的右行波, 即 \(\theta=\frac{\pi}{4}\).

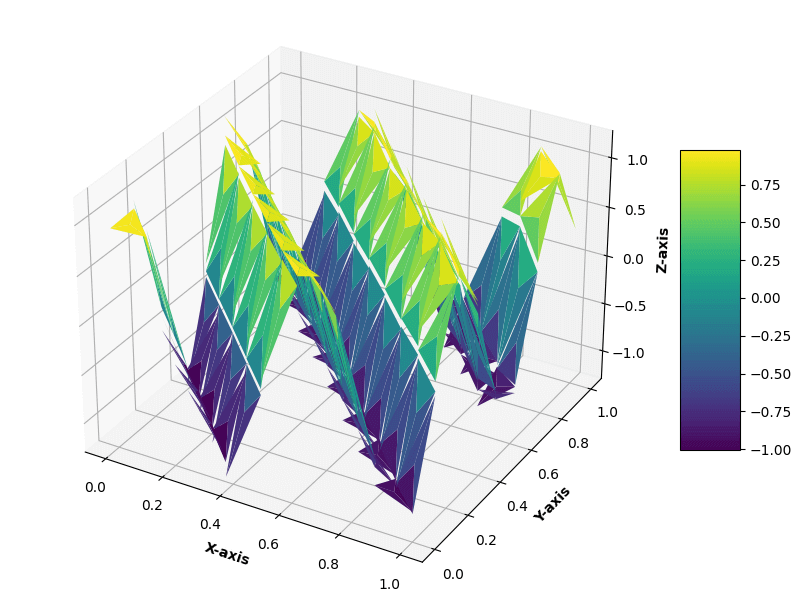
在数值计算中, 我们使用一致加细的三角形网格, 如图 1 为初始网格. 对于时间离散, 令时间步长 \(\Delta t=1/4000\). 在图 2 中, 我们画出了数值解 \(E_h\) 在时间 \(t=1\) 的图像. 同时, 我们也列出了误差 \(L^2\) 范数下的误差 \(E-E_h\):

t=1, L2 error
Mesh Level 1: 0.060609
Mesh Level 2: 0.010941
Mesh Level 3: 0.002167
Mesh Level 4: 0.000498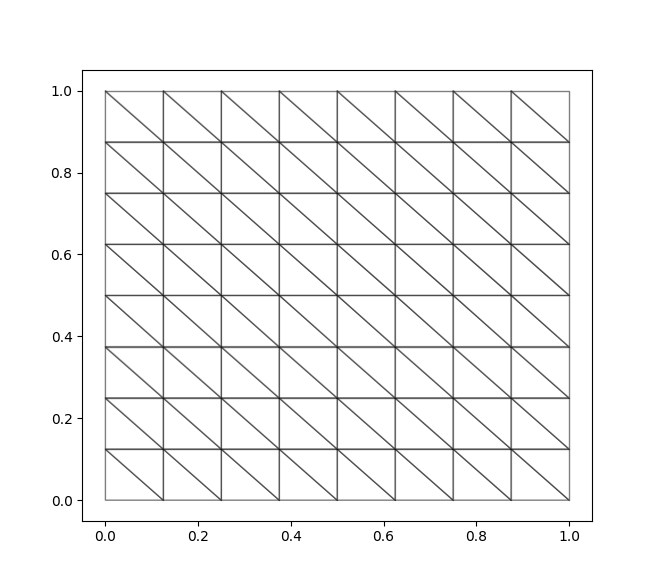

参考

[1] Hesthaven, J. S. and Warburton, T. (2008). Nodal Discontinuous Galerkin Methods (Vol. 54). Springer New York.
[2] Dosopoulos, S., Lee, J. F. (2010). Interior penalty discontinuous Galerkin finite element method for the time-dependent first order maxwell’s equations. IEEE Transactions on Antennas and Propagation, 58(12), 4085–4090.
[3] K. YEE, Numerical solutions of initial boundary value problems involving Maxwell’s equations in isotropic media, IEEE Trans. on Antennas and Propagation AP-16, pp. 302-307, 1966.

分享到: