Python 科学计算: SymPy
Python 因为开源免费, 语法简洁和第三方库众多等优点成为近年来的最流行的编程语言之一. 本文的主要目标是给出一些常用的符号计算示例和代码, 内容涉及数学分析的各个主题, 用来快速入门 Python 最常用的符号计算库 — Sympy.
基本用法
问题 Sympy 的最基本操作: 变量代换 (subs), 显式计算 (evalf) 和字符串转变为 Sympy 表达式 (sympify).
from sympy import symbols, sympify
from sympy import exp, sin
x, y, z = symbols('x y z')
expr = x + exp(x+y) + sin(z)
expr.subs(x,x*y)
expr.subs([(x,0),(y,1)])
(exp(1)).evalf()
expr_from_str = sympify("x**2+log(x)")
问题 多项式或者有理函数展开, 因式分解, 合并同类项, 简化等. 如:
- 将 \((x+2)^2+(x-3)^2\) 展开;
- 将 \(x^3-x^2+x-1\) 因式分解;
- 合并同类项: \(xy + x – 3 + 2x^2 – zx^2 + x^3\);
- 化简: \(\frac{x^3+x^2-x-1}{x^2+2x+1}\).
解 分别需要用到函数 expand, factor, collect, simplify. 代码如下.
from sympy import symbols
from sympy import expand, factor, collect, simplify
x,y,z = symbols('x y z')
expand( (x+2)**2+(x-3)**2 )
factor( x**3-x**2+x-1 )
collect( x*y+x-3+2*x**2-z*x**2+x**3, x )
simplify( (x**3+x**2-x-1)/(x**2+2*x+1) )
微积分
微分
问题 给定函数 \(u(x,y)=(x^2+y^2)^{a/2},a\neq 0\), 求 \(\nabla u\), \(-\Delta u\).
from sympy.abc import x,y,a from sympy import diff u = (x*x+y*y)**(.5*a) simplify( diff(u,x,1) ) simplify( diff(u,y,1) ) simplify( -diff(u,x,2)-diff(u,y,2) )
积分
问题 计算如下定积分和不定积分:
- \(\int x^2 dx \);
- \(\int_{0}^{\infty}e^{-x}dx\);
- \(\int_{0}^{\infty}e^{-x}dx\);
- \(\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-x^2-y^2}dxdy\);
from sympy import integrate, symbols
from sympy import exp, oo
x = symbols('x')
y = symbols('y')
integrate(x**2)
integrate(exp(-x), (x, 0, oo) )
integrate(exp(-x**2-y**2), (x, -oo, oo), (y, -oo, oo))
问题 考虑如下函数的 Fourier 变换\[ f(x) = \begin{cases} 1, & -1< x <1,\\ 0, & \text{otherwise}, \end{cases} \quad g(x)=\begin{cases} \cos (2x), & -\frac{\pi}{4}< x < \frac{\pi}{4},\\ 0, & \text{otherwise}. \end{cases}\]
解 利用 Fourier 变换的定义\[ \hat{f}(\omega)=\int_{-\infty}^{\infty }f(x) e^{-i x \omega} dx.\]可知, 对应的 Fourier 变换可以写成如下定积分的形式\[ \begin{align*} \hat{f}(\omega) &=\int_{-1}^{1 }e^{-i x \omega} dx =\begin{cases} \frac{\pi}{4} & \text{for}\: \omega = \pm 2, \\- \frac{4 \cos{\left(\frac{\pi \omega}{4} \right)}}{\omega^{2} – 4} & \text{otherwise}, \end{cases} \\ \hat{g}(\omega) &=\int_{-\pi/4}^{\pi/4 }\cos (2x) e^{-i x \omega} dx =\begin{cases} \frac{2 \sin{\left(\omega \right)}}{\omega} & \text{for}\: \omega \neq 0, \\2 & \text{otherwise}. \end{cases} \end{align*}\]
# fourier transform
from sympy import integrate, cos, exp, pi,I
from sympy import symbols, simplify,latex
x, omega = symbols("x omega", real=True)
# F=integrate(cos(2*x)*exp(-I*x*omega),(x, -pi/4, pi/4))
F=integrate(exp(-I*x*omega),(x, -1, 1))
simplify(F)
极限
问题 计算如下极限:
- \(\lim_{x\to 0}\frac{\sin(x)}{x}\);
- \(\lim_{x\to 0}(1+x)^{\frac{1}{x}}\);
- \(\lim_{x\to 0} \frac{a^x+a^{-x}-2}{x^2}(a>2) \);
- \(\lim_{x\to \pi} \frac{1+\cos(x)}{\tan^2(x)} \);
Python 代码如下, 其中主要的求极限函数为 limit(f, z, z0, dir='+').
# limit from sympy.abc import x, a from sympy import limit, sin limit(sin(x)/x, x, 0) limit((1+x)**(1/x), x, 0) limit((a**x+a**(-x)-2)/(x*x), x, 0) limit((1+cos(x))/(tan(x)**2), x, pi)
级数展开
问题 计算如下函数在 \(x=0\) 处的级数展开:
- \(e^x\);
- \(\log(1+x)\);
- \(\sin(x) \);
- \(\frac{1}{1+x} \);
Python 代码如下, 其中用到的级数函数为 series(expr, x, x0, n).
# f(x).series(x, x0, n) from sympy.abc import x from sympy import exp, log, sin from sympy import series series(exp(x), x, 0, 8) series(log(1+x), x, 0, 8) sin(x).series(x, 0, 8) (1/(1+x)).series(x, 0, 8)
方程求解
代数方程
问题 求方程 \( x^2-x+1=0\) 和 \(x^2-x+1=0\) 的实根.
解 代数方程的求解函数主要是 solveset, 其语法为 solveset(equation, variable=None, domain=S.Complexes). 第一个方程的根可以直接计算如下 $$ \left\{\frac{1}{2} – \frac{\sqrt{5}}{2}, \frac{1}{2} + \frac{\sqrt{5}}{2}\right\}= \left\{-0.618033988749895, 1.61803398874989\right\}. $$ 第二个方程的实根为 $$ x=\frac{1}{3 \sqrt[3]{\frac{\sqrt{69}}{18} + \frac{1}{2}}} + \sqrt[3]{\frac{\sqrt{69}}{18} + \frac{1}{2}}=1.32471795724475, $$ 可以用数值方法, 如二分法, 最速下降法或者牛顿法来近似求解. sympy 的求解代码如下.
# solver from sympy.abc import x from sympy import sin from sympy import solveset solveset(x**2 - x - 1, x) solveset(x**3 - x - 1, x).evalf()
问题 求如下线性或非线性系统.
- \( x+y+z-1=0, x+y+2z-3=0 \);
- \( x^2+x=0, x-y=0 \).
解 线性或非线性系统的求解函数分别为 linsolve 和 nonlinsolve.
# solver
from sympy.abc import x,y,z
from sympy import Matrix
from sympy import linsolve, nonlinsolve
linsolve([x + y + z - 1, x + y + 2*z - 3 ], (x, y, z))
linsolve(Matrix([[1, 1, 1, 1], [1, 1, 2, 3]]), (x, y, z))
nonlinsolve([x**2+x, x-y], (x,y))
常微分方程
问题 设常数 \(a\geq 0\), 如下常微分方程 $$ f^{\prime\prime}(x)+x^{-1}f^{\prime}(x) -a^2 x^{-2} f(x)=0 $$
解 通解为 当 \(a=0\) 时, \(f(x)=c_1+c_2\log(x)\); 当 \(a>0\) 时, \(f(x)=c_1 x^a+c_2 x^{-a}\).
from sympy import Function, dsolve, Eq, symbols
from sympy.abc import x, a
# a = 0
v = symbols('v', cls=Function)
diff_eq = Eq( v(x).diff(x,x)+v(x).diff(x)/x-a**2*v(x)/x/x, 0)
dsolve(diff_eq, v(x))
代数运算
矩阵是 Sympy 中重要的数据结构, 具备完善的线性代数的运算能力, 同时矩阵类中的元素也可以像 numpy 中的矩阵一样进行索引以及支持标准的矩阵运算, 如 +, -, *, **. 需要注意的是, Numpy 中的算术运算 (乘法 * 和幂运算 `**`) 是矩阵逐元素运算, 但是 Sympy 中的运算是标准的矩阵运算. 可以用类似如下语句载入 from sympy import eye 相关函数, 常用的函数如下
| 通用函数 | |
| eye | eye(n): 生成 n 阶单位矩阵 |
| zeros | zeros(n,m): 生成 n*m 阶零矩阵 |
| ones | ones(n,m): 生成 n*m 阶全1矩阵 |
| Matrix | Matrix([ [1, 2], [2,1] ] ): 生成矩阵 \( [1 , 2; 2, 1] \) |
| diag | diag(x,y,z): 生成对角矩阵 \([x, 0,0; 0, y, 0; 0,0,y]\) |
| +,-,*,** | \( A-B, A+B, A*B, A**2 \) |
| GramSchmidt() | 将向量列表 L 进行 Gram-Schmidt 正交化 |
| 矩阵类常用方法: 代数运算 | |
| A.inv() | 矩阵求逆 |
| A.pinv() | 矩阵伪逆 (Moore-Penrose pseudoinverse) |
| A.det() | 矩阵行列式 |
| A.norm() | 矩阵范数: None 或 2, ‘fro’, inf, 1 等 |
| A.condition_number() | 矩阵条件数 |
| A.QRdecomposition() | QR 分解, 返回矩阵 Q, R 使得 A=QR |
| A.cholesky() | Cholesky 分解, 返回矩阵 L 使得 A=LL^t |
| A.LDLdecomposition() | LDL^t 分解, 返回矩阵 L, D 使得 A=LDL^t |
| A.LUdecomposition() | LU 分解, 返回矩阵 L, U, perm 使得 A=(L*U).permuteBkwd(perm) |
| A.LUsolve(b) | 求解线性系统 Ax=b |
| A.subs() | A.subs(x,4), 矩阵中的 x 代换 为 4 |
| A.dot() | A.dot(v), 矩阵向量乘积 |
| A.cross() | A.cross(v), 向量叉乘 |
| A.row_join() | A.row_join(B), 横向合并矩阵 [A, B] (A,B必须是相同行数) |
| A.col_join() | A.col_join(B), 纵向合并矩阵 [A; B] (A,B必须是相同列数) |
| A.eigenvals() | 计算特征值 |
| A.eigenvects() | 计算特征向量和特征值 |
| A.charpoly() | 计算特征多项式 det(\(\lambda I- A\)) |
| A.minor(i,j) | 计算矩阵的 (i,j) 余子式 |
| A.columnspace() | 返回矩阵的列向量空间 (一个向量列表) |
| A.rowspace() | 返回矩阵的行向量空间 (一个向量列表) |
| A.nullspace() | 返回矩阵的零空间 (一个向量列表) |
| A.diagonalize() | 对角化矩阵, 返回矩阵 P, D 使得 D=P^{-1} A P |
| A.is_diagonalizable() | 检查矩阵是否可对角化 |
| A.jordan_form() | 矩阵的 Jordan 形, 返回矩阵 $P, J$ 使得 $A=P J P^{-1}$ |
| A.is_positive_definite | 检查矩阵是否是正定的 |
| A.is_positive_semidefinite | 检查矩阵是否是半正定的 |
| A.is_indefinite | 检查矩阵是否是不定的 |
| 矩阵类常用方法: 符号运算 | |
| A.diff() | A.diff(x) 矩阵元素微分 |
| A.limit() | A.limit(x,0) 矩阵元素计算极限 |
| A.integrate() | A.integrate(x, 0, 1) 矩阵元素积分 |
| A.jacobian() | 计算向量值函数的 Jacobian 矩阵 |
| A.applyfunc(f) | A.applyfunc(f), 将函数 f 作用于矩阵中的所有元素 |
问题 如何使用 jacobian()?
from sympy import sin, cos, Matrix from sympy.abc import rho, phi X = Matrix([rho*cos(phi), rho*sin(phi), rho**2]) Y = Matrix([rho, phi]) X.jacobian(Y)
问题 给定极坐标函数 \(u(r,\theta)=r^a \sin(a\theta), a\neq 0\), 求其在笛卡尔坐标下的梯度及 Laplace 算子 \(\nabla u\), \(-\Delta u\).
解 首先, 注意到极坐标变换 $$ x(r,\theta)=r\cos(\theta),\ y(r,\theta)=r\sin(\theta), $$ 简单计算可知 \[ \nabla_{r,\theta} u= J^T \nabla_{x,y}u, \] 这里 \(J\) 为 Jacobian 矩阵 \[ J = \begin{bmatrix}\frac{dx}{dr} & \frac{dx}{d\theta}\\ \frac{dy}{dr} & \frac{dy}{d\theta} \end{bmatrix} =\begin{bmatrix}\cos(\theta) & -r\sin(\theta)\\ \sin(\theta) & r\cos(\theta) \end{bmatrix}. \] 因此, \[ \nabla_{x,y}u = J^{-T} \nabla_{r,\theta} u, \quad J^{-T} =\begin{bmatrix}\cos(\theta) & -\frac{1}{r}\sin(\theta)\\ \sin(\theta) & \frac{1}{r}\cos(\theta) \end{bmatrix}. \]
import sympy
from sympy.abc import r,t,a
from sympy import sin, cos, symbols, diff, Matrix, simplify
xrt, yrt = r*cos(t), r*sin(t)
u = r**a * sin(a*t)
grad_rt = Matrix([u.diff('r'), u.diff('t')]).applyfunc(simplify)
J_T = Matrix([[diff(xrt,'r'), diff(xrt,'t')],[diff(yrt,'r'), diff(yrt,'t')]]).T
inv_J_T = J_T.inv()
inv_J_T.applyfunc(simplify)
grad = inv_J_T * grad_rt
grad.applyfunc(simplify)
问题 在考虑一阶 Maxwell 方程的非反射边界条件时, 如果使用 Laplace-Fourier 变换, 那么经常会遇到如下线性系统\[ \begin{equation*} \partial_{x_1} \begin{bmatrix} \hat{u}_2\\ \hat{u}_3\\ \hat{u}_5\\ \hat{u}_6 \end{bmatrix} = \begin{bmatrix} & & \frac{\omega_2\omega_3}{s} & -\left( s+\frac{\omega_2^2}{s} \right) \\ & & \left( s+\frac{\omega_3^2}{s} \right) & -\frac{\omega_2\omega_3}{s} \\ -\frac{\omega_2\omega_3}{s} &\left( s+\frac{\omega_2^2}{s} \right) & & \\ -\left( s+\frac{\omega_3^2}{s} \right)& \frac{\omega_2\omega_3}{s} & & \end{bmatrix}\begin{bmatrix} \hat{u}_2\\ \hat{u}_3\\ \hat{u}_5\\ \hat{u}_6 \end{bmatrix}=:N \begin{bmatrix} \hat{u}_2\\ \hat{u}_3\\ \hat{u}_5\\ \hat{u}_6 \end{bmatrix}.\end{equation*}\]请问如何对角化矩阵 \(N\)?
解 利用函数 diagonalize(). 代码如下:
# matrix diagonalization
from sympy import symbols, zeros, Matrix, simplify
s, omega2, omega3 = symbols('s omega2 omega3')
# N
N1 = Matrix([[omega2*omega3/s, -(s+omega2**2/s)],[(s+omega3**2/s), -omega2*omega3/s]])
N = Matrix([[zeros(2,2), N1],[-N1,zeros(2,2)]])
(P,D) = N.diagonalize() # N= PDP^{-1}
可视化
Sympy 绘图模块允许您制作二维和三维图。 目前,使用 Matplotlib 作为后端呈现绘图, 主要函数有:
plot: Plots 2D line plots.plot_parametric: Plots 2D parametric plots.plot_implicit: Plots 2D implicit and region plots.plot3d: Plots 3D plots of functions in two variables.plot3d_parametric_line: Plots 3D line plots, defined by a parameter.plot3d_parametric_surface: Plots 3D parametric surface plots.
Plot
Sympy 中的 Plot 类是绘图功能的核心模块, 当利用绘图函数, 如 plot 函数, 绘图时就会返回一个 Plot 类. 下面的代码展示了绘图函数的基本用法
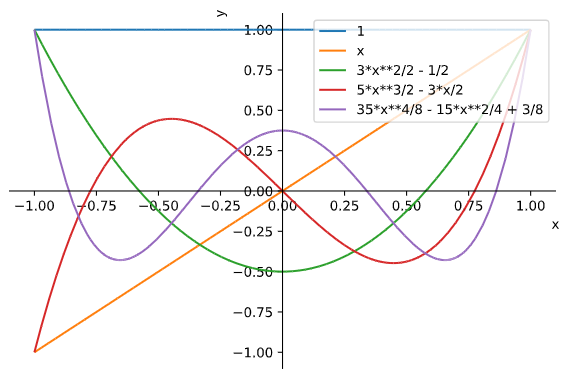
例 利用 Sympy 画出前五个 Legendre 多项式的图像.
解 Legendre 多项式的前五个成员分别如下 $$1, \ x,\ \frac{1}{2}(3x^2-1),\ \frac{1}{2}(5x^3-3x), \ \frac{1}{8}(35x^4-30x^2+3). $$
# 单变量函数绘图 (version 1)
from sympy import symbols
from sympy.plotting import plot
x = symbols('x')
p1 = plot(1, x, (3*x**2-1)/2, (5*x**3-3*x)/2, (35*x**4-30*x**2+3)/8, (x,-1,1), show=False)
p1.title = 'Legendre Polynomials'
p1[0].line_color = 'pink'
p1[1].line_color = 'salmon'
p1[2].line_color = 'tan'
p1[3].line_color = 'wheat'
p1[4].line_color = 'olive'
p1.legend = True
p1.ylabel = 'p(x)'
p1.xlabel = 'x'
p1.show()
注意, 上面代码中颜色的选择可以有多种形式, 例如可以使用 RGB 元组 line_color = (1.0, 0, 0) 或者十六进制 line_color = #0f0f0f 等等, 具体可以参考 Matplotlib: Specifying Colors. 下面的代码实现更为简洁, 直接利用 Sympy 中内置的 Legendre 多项式函数. 同时也使用了 Plot 类的 append 方法或者 extend 方法.
# 单变量函数绘图 (version 2)
from sympy import symbols, legendre
from sympy.plotting import plot
x = symbols('x')
p = plot(show=False) # make an empty Plot
for i in range(5):
p2 = plot(legendre(i,x), (x,-1,1), line_color = f'C{i}', show=False)
# p.append(p2[0]) # add data from Plot instance 'p2'
p.extend(p2) # add data from Plot instance 'p2', 效果与上面的append相同
p.legend = True
p.ylabel = 'y'
p.xlabel = 'x'
p.show()
参数函数绘图
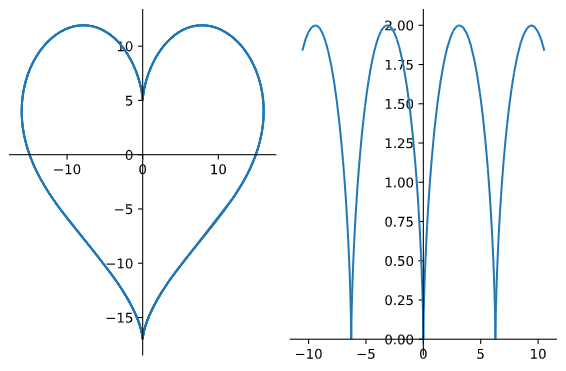
例 绘制满足如下参数方程的曲线图像:
- 心形曲线: \( x=16\sin^3(t),\ y=13\cos(t)-5\cos(2t)-2\cos(3t)-\cos(4t) \);
- 摆线: \( x=r(t-\sin(t)),\ y=r(1-\cos(t)) \);
from sympy import symbols, cos, sin
from sympy.plotting import plot_parametric
t = symbols('t')
plot_parametric((16*sin(t)**3, 13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t) ))
plot_parametric((1*(t-sin(t)), 1*(1-cos(t)) ))
隐函数绘图
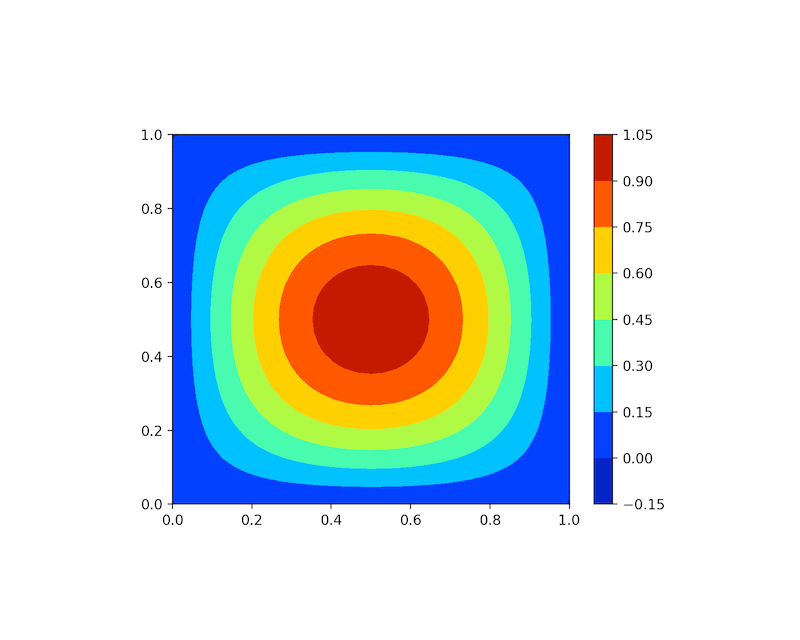
例 隐函数绘图使用函数 plot_implicit, 可以传入等式者不等式. 绘制如下等式者不等式函数的图像:
- \((x^2+y^2-1)^3-x^2y^3=0\);
- \(y>x^2\).
from sympy import plot_implicit, Eq
from sympy import symbols
x, y = symbols('x y')
# p1 = plot_implicit(Eq(x**2 + y**2, 5), (x, -3, 3), (y, -3, 3))
p1 = plot_implicit((x**2 + y**2-1)**3-x**2 * y**3, (x, -1.5, 1.5), (y, -1.5, 1.5))
三维绘图
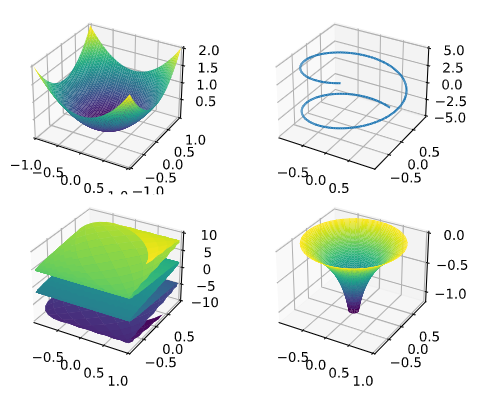
例 绘制如下函数的图像:
- \(f(x,y)=x^2+y^2\);
- \((x,y,z)=(\cos(u), \sin(u),u), \ u\in [-5,5]\);
- \((x,y,z) = (\cos(u+v), \sin(u-v), u-v,\ u\in[-5,5], v\in [-5,5] \);
- \((x,y,z) = (r\cos(t), r\sin(t), \log(\sqrt{r})),\ r\in[0.1,1], t\in [0,2\pi]\).
from sympy import symbols, pi, sin, cos, log
from sympy.plotting import plot3d, PlotGrid
from sympy.plotting import plot3d_parametric_line
from sympy.plotting import plot3d_parametric_surface
x, y=symbols('x y')
u,v = symbols('u v')
r,t = symbols('r t')
p1 = plot3d(x**2+y**2, (x, -1, 1), (y, -1, 1), show=False)
p2 = plot3d_parametric_line(cos(u), sin(u), u, (u, -5, 5), show=False)
p3 = plot3d_parametric_surface( cos(u+v), sin(u-v), u-v, (u, -5, 5), (v, -5, 5), show=False)
p4 = plot3d_parametric_surface( r*cos(t), r*sin(t), log(r**(1/2)), (r, .1, 1.), (t, 0, 2*pi), show=False)
PlotGrid(2, 2, p1, p2, p3, p4)
总结
Sympy 还具有很多其它应用, 如几何, PDE, 张量, 统计等等, 关于更多信息和更详细的使用教程请参考官方文档. 相比于 Matlab 的符号计算工具箱, Sympy 功能也是相当强大, 并且更加轻量和具有极高的可移植性, 参考Matlab vs Sympy.
附录
安装和运行环境
安装: pip3 install sympy
Python 环境: vscode + Python + Jupyter
输出方式
Python 环境中, Sympy 提供多种输出方式, 例如 ASCII, LaTeX, MathML 等. 在 vscode 中新建 *.ipynb 文件, 并输入如下代码
from sympy.abc import x
from sympy import exp, series
expr = series(exp(x), x, 0, 8) # e^x 的级数展开
expr
结果:
$$ 1 + x + \frac{x^{2}}{2} + \frac{x^{3}}{6} + \frac{x^{4}}{24} + \frac{x^{5}}{120} + \frac{x^{6}}{720} + \frac{x^{7}}{5040} + O\left(x^{8}\right)$$
如果安装了 LaTeX, Sympy 会直接利用 LaTeX 引擎渲染结果, 如上图. 如果没有, 那么会尝试利用 Matplotlib 来渲染结果. 如果这两个都没有, 则会利用精致的字符串生成结果. 例如, 从 sympy 中导入初始化输入函数 from sympy import init_printing, 并添加如下代码禁用 LaTeX init_printing(use_latex=False), 就会有如下输出

Sympy 输出 LaTeX 代码
Sympy 还可以利用 latex() 输出 LaTeX 源码, 例如, 在上面的示例代码中添加 print(latex(expr)), 会输出结果的 LaTeX 代码 (别忘记 from sympy import latex)
1 + x + \frac{x^{2}}{2} + \frac{x^{3}}{6} + \frac{x^{4}}{24} + \frac{x^{5}}{120} + \frac{x^{6}}{720} + \frac{x^{7}}{5040} + O\left(x^{8}\right)
Sympy 输出 MathML 代码
Sympy 还可以利用 print_mathml() 输出 MathML 源码, 例如, 在上面的示例代码中添加 print_mathml(expr), 即可 (别忘记 from sympy import print_mathml).
Sympy 输出 Python 代码
Sympy 还可以利用 python() 输出 Python 源码, 例如, 在上面的示例代码中添加 print(python(expr)), 即可 (别忘记 from sympy import python).
参考文献
[1] SymPy Tutorial.