Gmsh 极简入门
Gmsh is a free 3D finite element mesh generator with a built-in CAD engine and post-processor. Its design goal is to provide a fast, light and user-friendly meshing tool with parametric input and advanced visualization capabilities. Gmsh is built around four modules: geometry, mesh, solver and post-processing. The specification of any input to these modules is done either interactively using the graphical user interface, in ASCII text files using Gmsh’s own scripting language (.geo files), or using the C++, Python or C API.
Gmsh 是一个开源的具有内置 CAD 引擎和后期处理子的三维有限元网格生成器.
- 它的目的是提供一个快速的, 轻量级的, 用户友好的网格工具, 并且具有参数化输入和后期可视化能力. 目前 Gmsh 具有四个模块: 几何模块, 网格模块, 解子模块和后期处理模块, 且所有模块的使用都可以通过两种方式: 命令行和 GUI. 有限元网格生成工具有很多种, 比如 MeshGen, Hypermesh, 以及一个 MATLAB 小工具 DistMesh, 等等.
- Gmsh 提供 Linux, Mac and Windows 版本, 并且在下载的安装包的 tutorial 目录中包含一个介绍关键概念和一些实例的教程. 这个教程里的实例都有非常详细的脚本注释, 易于入门, 是学习 Gmsh 的第一步.
为什么需要网格
网格生成 (Mesh generation or grid generation) 又可以称为网格剖分, 即将一个有界的连续的几何空间划分成由有限个单纯形, 矩形, 多边形或多面体构成的离散的几何空间, 是有限元方法求解偏微分方程的第一步. 高质量的网格往往依赖于求解区域及方程特性, 同时一般能够带来更精确的有限元解.
表示网格最简单的数据结构应该就是 单元-节点 结构, 例如 \([0,1]\times[0,1]\) 上一个简单的三角形网格可以由两个变量表示 points 和 elements:
points = # 所有节点的坐标(x, y, z), 对二维空间 z=0
[[0. 0. 0. ] # vertice 0
[1. 0. 0. ] # vertex 1
[1. 1. 0. ] # vertex 2
[0. 1. 0. ] # vertex 3
[0.5 0.5 0. ]] # vertex 4
elements = # 每一个网格单元由那些节点构成, 一般节点按逆时针排序
[[0 1 4] # element 0
[3 0 4] # element 1
[1 2 4] # element 2
[2 3 4]] # element 3对于简单的求解区域, 例如 \([0,1]\times[0,1]\), 我们可以很容易划分一个三角形网格, 甚至直接写出 C 或者 Python 代码生成网格. 但是, 当求解区域是一个复杂多边形或边界是光滑曲线时, 手动生成网格就变得相当困难或者烦琐, 借助相关的网格生成软件或程序是必须的. 考虑到求解区域复杂度, 网格单元分类, 网格单元大小及形状正则性, 网格加细等等, 可以想象关于网格生成是相当有挑战性的研究方向, 有相当多的会议和研讨会将网格生成作为议题, 还有不少知名杂志持续地接收关于网格生成的研究成果, 更多介绍请参考维基百科: Mesh generation.
好消息是, 如果不是专门做网格生成的研究, 我们只需利用现成的网格生成工具, 如 Gmsh, 来生成需要的网格.
如何使用 Gmsh
如果你是第一次利用 Gmsh 生成网格, 可以参考如下几步:
- 官网下载并安装最新版 Gmsh. 无论你用 Win, MacOS 还是 Linux, Gmsh 均提供相应二进制文件;
- 正确编写 *.geo 脚本文件. tutorial 目录下有许多脚本示例, 非常适合入门; 或者以下面的脚本作为第一个例子. 新建空白文本文档 unitSquare.geo, 拷贝如下内容并保存:
// unit square // len = 1.; //Mesh size Point(1) = {0,0,0,len}; Point(2) = {1,0,0,len}; Point(3) = {1,1,0,len}; Point(4) = {0,1,0,len}; Line(1) = {1,2}; Line(2) = {2,3}; Line(3) = {3,4}; Line(4) = {4,1}; Line Loop(5) = {1,2,3,4}; Plane Surface(1) = {5}; // 生成标准三角元,最后的参数可以是Left, Right, 或者Alternate //Transfinite Surface{1}={1,2,3,4} Alternate; // 通过合并三角元生成标准矩形元 // Recombine Surface{1}; Physical Line(1) = {2,4}; Physical Surface(2) = {1}; - 在 Gmsh 中打开该文件, 界面左边找到
Modules->Mesh->2D并点击; 然后点击File-> Save mesh, 就可以在相同文件夹下生成同名网格文件 unitSquare.msh;
我们需要的网格 (points 和 elements) 就存储在文件 unitSquare.msh 中, 下一步就是提取这些数据 (后面有介绍) 并应用在有限元程序或其它程序中.
msh 文件
Gmsh 生成的 *.msh 文件中保存了全部网格信息, 也就完成了网格生成的任务. *.msh 文件的详细解释请参考官网: MSH 文件格式. 除了官网给出的教程中包含的 GEO 文件示例外, 更多的例子可以参考 Visual Description of GMSH Tutorials. 上面的 .geo 脚本生成的 MSH 文件 unitSquare.msh 如下 (Gmsh 4.4.1):
$MeshFormat
4.1 0 8
$EndMeshFormat
$Entities
4 4 1 0
1 0 0 0 0
2 1 0 0 0
3 1 1 0 0
4 0 1 0 0
1 0 0 0 1 0 0 0 2 1 -2
2 1 0 0 1 1 0 1 1 2 2 -3
3 0 1 0 1 1 0 0 2 3 -4
4 0 0 0 0 1 0 1 1 2 4 -1
1 0 0 0 1 1 0 1 2 4 1 2 3 4
$EndEntities
$Nodes
7 5 1 5
0 1 0 1
1
0 0 0
0 2 0 1
2
1 0 0
0 3 0 1
3
1 1 0
0 4 0 1
4
0 1 0
1 2 0 0
1 4 0 0
2 1 0 1
5
0.5 0.5 0
$EndNodes
$Elements
3 6 1 6
1 2 1 1
1 2 3
1 4 1 1
2 4 1
2 1 2 4
3 1 2 5
4 4 1 5
5 2 3 5
6 3 4 5
$EndElements使用 CAD 文件
Gmsh 可以直接导入 CAD 文件并生成 2D/3D 网格, 并且可以在用户界面直接修改网格参数并指定网格大小, 一个相关教程可以参考 [Gmsh CAD File Import and Mesh Generation Tutorial]. 下图是从文件 8871T32.STEP 文件导入生成的网格示意图, 文件是从 [https://www.servocity.com] 下载的, 非常感谢. 另外, Gmsh 可以从导入的 STEP 文件导出 GEO 脚本文件, 从而需要的话, 可以在 geo 文件中对模型参数进行修改.
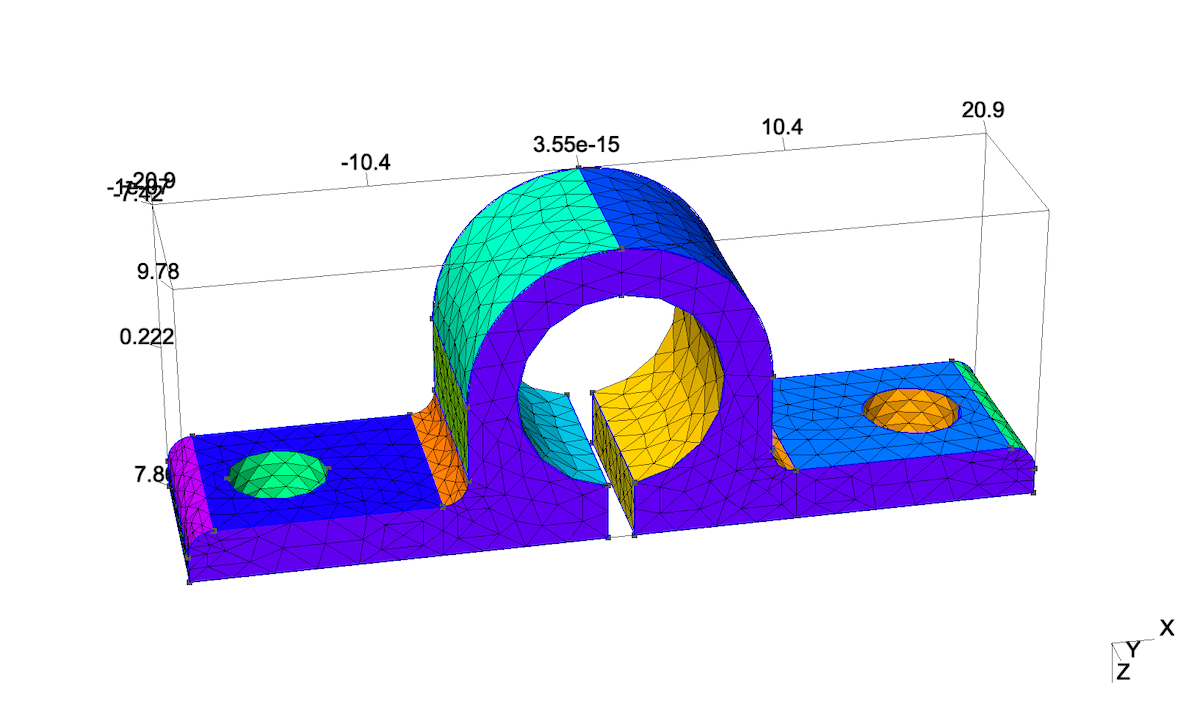
Python 中使用 Gmsh
利用 meshio
Meshio 是 Python 下的标准模块, 可以读写许多网格文件格式, 例如:
Abaqus, ANSYS msh, AVS-UCD, CGNS, DOLFIN XML, Exodus, FLAC3D, H5M, Kratos/MDPA, Medit, MED/Salome, Nastran (bulk data), Neuroglancer precomputed format, Gmsh (format versions 2.2, 4.0, and 4.1), OBJ, OFF, PERMAS, PLY, STL, Tecplot .dat, TetGen .node/.ele, SVG (2D only, output only), SU2, UGRID, VTK, VTU, WKT (TIN), XDMF.
— https://pypi.org/project/meshio/
Meshio 模块的使用非常简单, 官网有详细的说明: https://pypi.org/project/meshio/. 利用 meshio 读取上面的文件 unitSquare.msh 的程序如下:
import meshio
import numpy as np
mesh = meshio.read('./unitSquare.msh', \
file_format='gmsh')
# 保存数据或打印, 或者提供给其它使用网格的程序, 如有限元等等
# np.savetxt('points.txt', mesh.points)
# np.savetxt('cells.txt', mesh.cells['triangle'])
print(mesh.points,'\n', mesh.cells_dict['triangle'])
print('\n')
# 输出如下:
# [[0. 0. 0. ]
# [1. 0. 0. ]
# [1. 1. 0. ]
# [0. 1. 0. ]
# [0.5 0.5 0. ]]
# [[0 1 4]
# [3 0 4]
# [1 2 4]
# [2 3 4]]
当网格数据被提取并保存在文本文件里之后, 其它的程序语言如 Matlab, C/C++, Scilab 或者 R 等, 均可以利用这些网格数据.
利用 pygmsh
如果你以 Python 做为生产力编程语言, 并且需要用到网格, 那么就非常有必要了解一下 Pygmsh. 它的目的是提供 Gmsh 的 Python 接口, 并改进一些直接利用 Gmsh 的缺点.
- 例如在 Gmsh 脚本中每一个几何实体 (点, 线, 面等) 必须手动分配一个编号 (1, 2, …), 并且必须检查这些编号是唯一的, 但是如果利用 Pygmsh, 这些几何实体可以变量名命名 (点可以用 p1, p2, …命名, 线为 l1, l2, …), 这样就避免了对编号是否唯一的检查.
#! /usr/bin/env python3
# 在矩形 [0,1]*[0,1] 上生成三角形网格
#
import pygmsh
import meshio
import numpy as np
# 构造一个空的几何体数据结构
#
with pygmsh.geo.Geometry() as geom:
geom.add_rectangle(0.0, 1.0, 0.0, 1.0, 0.0, 0.1)
mesh = geom.generate_mesh()
#
# 生成网格 mesh, 其具有数据结构:
# |- mesh.points # coordinates of nodes (N*3)
# |- mesh.cells_dict['line'] # mesh edges (N*2)
# |- mesh.cells_dict['triangle'] # triangles (N*3)
#
#
# 保存数据或打印, 或者提供给其它使用网格的程序, 如有限元等等
# np.savetxt('points.txt', mesh.points)
# np.savetxt('cells.txt', mesh.cells_dict['triangle'])
#
print(mesh.points)
print(mesh.cells_dict['triangle'])
更多的网格示例
结构和非结构混合网格
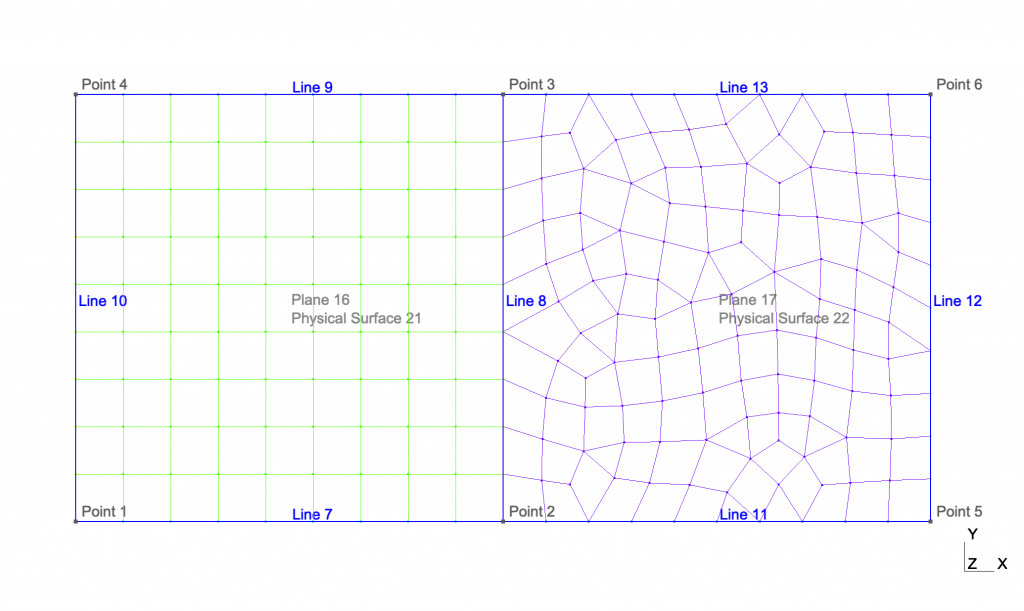
其中, 区域左半剖分由结构网格构成, 右半剖分由非结构网格构成, 可以明显看出, 两部分构成了一个拟一致网格. GEO 脚本源代码和 Python 代码如下:
//http://www.cfdyna.com/Home/gmshCatalogue.html
boxdim = 1;
gridsize = boxdim/10;
Point(1) = {0,0,0,gridsize};
Point(2) = {boxdim,0,0,gridsize};
Point(3) = {boxdim,boxdim,0,gridsize};
Point(4) = {0,boxdim,0,gridsize};
Point(5) = {2*boxdim,0,0,gridsize};
Point(6) = {2*boxdim,boxdim,0,gridsize};
Line(7) = {1,2};
Line(8) = {2,3};
Line(9) = {3,4};
Line(10) = {4,1};
Line(11) = {2,5};
Line(12) = {5,6};
Line(13) = {6,3};
Line Loop(14) = {7,8,9,10};
Line Loop(15) = {11,12,13,-8};
Plane Surface(16) = 14;
Plane Surface(17) = 15;
//Make one square structured.
Transfinite Line{7,8,9,10} = boxdim/gridsize;
Transfinite Surface{16};
Recombine Surface{16};
Recombine Surface{17};
# Unstructured and Structured Hybrid Meshes
# refer geo mesh from http://www.cfdyna.com/Home/gmshCatalogue.html
import gmsh
import sys
from pathlib import Path
boxdim = 1
gridsize = boxdim/10
gmsh.initialize()
gmsh.model.add('hybrid_mesh')
f = gmsh.model.geo
f.addPoint(0,0,0,gridsize,1)
f.addPoint(boxdim, 0,0,gridsize,2)
f.addPoint(boxdim,boxdim,0,gridsize,3)
f.addPoint(0,boxdim,0,gridsize,4)
f.addPoint(2*boxdim, 0,0,gridsize,5)
f.addPoint(2*boxdim, boxdim,0,gridsize,6)
f.addLine(1, 2, 7)
f.addLine(2, 3, 8)
f.addLine(3, 4, 9)
f.addLine(4, 1, 10)
f.addLine(2, 5, 11)
f.addLine(5, 6, 12)
f.addLine(6, 3, 13)
f.addCurveLoop([7,8,9,10], 14)
f.addCurveLoop([11,12,13,-8], 15)
f.addPlaneSurface([14], 16)
f.addPlaneSurface([15], 17)
# Make one square structured.
for i in range(7,11):
f.mesh.setTransfiniteCurve(i, int(boxdim/gridsize))
f.mesh.setTransfiniteSurface(16, "Alternate")
f.mesh.setRecombine(2, 16)
f.mesh.setRecombine(2, 17)
# Physical surface
f.addPhysicalGroup(2, [16], 21)
f.addPhysicalGroup(2, [17], 22)
f.synchronize()
gmsh.model.mesh.generate(2)
# write mesh to MSH file in the same folder
folder_name = str(Path(__file__).resolve().parent) + '/'
gmsh.write(folder_name+"hybrid_mesh.msh")
if '-nopopup' not in sys.argv:
gmsh.fltk.run()
gmsh.finalize()
注意:
- 非结构网格中同时包含三角形和四边形两种网格单元, 在使用网格时需要多注意;
- 通过上述两个脚本文件生成的 msh 网格文件同样可以由 Python 包 meshio 来读取, 并且可以保留下来每个单元所在物理区域的信息.
花瓣界面网格
给出一个生成花瓣界面网格的 GMSH 示例. 花瓣界面的网格可用于验证求解二阶椭圆界面问题的算法的有效性, 利用 Gmsh 内置的脚本文件可以轻易生成具有复杂形状的界面, 这使得Gmsh成为生成各种网格的一个非常实用工具. 下面给出具体示例。目的是在区域 \([-1,1]\times[-1,1]\) 上生成一个五叶花瓣界面,其表达式如下: $$ r = \frac{1}{2} + \frac{\sin( 5\theta )}{7},\quad \theta\in[0,\ 2\pi]. $$ 容易知道其外法向量为 \(n=\frac{(y'(\theta), -x'(\theta))}{\sqrt{x'(\theta)^2+y'(\theta)^2}}\), 这里 \(x=r\cos(\theta),y=r\sin(\theta)\). 其图形如下图所示.
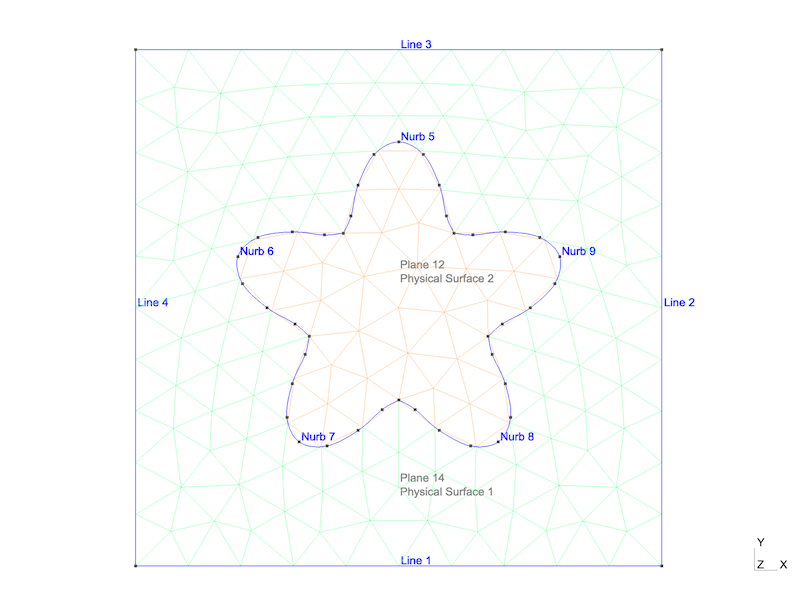
生成上图的脚本文件如下所示, 这里要注意两个地方: 1. 生成五叶花瓣的循环;2. Coherence去掉重复的点.
/*
* To generate petal interface in square [-1,1]^2, and the interface is
* parametrized with the polar angle 'theta' [1]:
* r = 1/2 + Sin( 5* theta ) / 7, [0, 2*pi].
*/
ls = .2;
nPoints = 9; // Number of points in one petal
start = Pi/2-2*Pi/10; end = Pi/2+2*Pi/10;
step = (end-start)/(nPoints-1);
Point(1) = {-1,-1,0,ls}; Point(2) = {1,-1,0,ls};
Point(3) = {1,1,0,ls}; Point(4) = {-1,1,0,ls};
Line(1) = {1,2}; Line(2)={2,3}; Line(3)={3,4}; Line(4)={4,1};
For k In {0:4} // Five petal
start = Pi/2-Pi/5 + k*2*Pi/5; // the Position of each petal
For i In {0:nPoints-1}
theta = start + step*i;
pList[i] = newp;
Point(pList[i]) = {(0.5+Sin(5*theta)/7)*Cos(theta),
(0.5+Sin(5*theta)/7)*Sin(theta),0,ls};
EndFor
petalLines[k] = newl;
Spline(petalLines[k]) = pList[]; //Creates spline curve, i.e., a petal.
EndFor
Coherence; //Delete all duplicate elementary geometrical entities(Points here).
Line Loop(11) = petalLines[]; Plane Surface(12) = {11};
Line Loop(13) = {1,2,3,4}; Plane Surface(14) = {13,11};
Physical Surface(1)={14}; // Exterior part '1'
Physical Surface(2)={12}; // Interior part '2'FEM 字母网格

//Generate a mesh on the cover of the book:
//Brenner, S. C., & Scott, L. R. (2008). The Mathematical Theory of Finite Element Methods (Third).
//
s=.5;
Point(1) = {0, 0, 0,s}; Point(2) = {1.35,0, 0,s};
Point(3) = {1.35, 2.15, 0,s}; Point(4) = {2.20, 3.05, 0,s};
Point(5) = {2.20, 4.80, 0,s}; Point(6) = {1.35, 5.75, 0,s};
Point(7) = {1.35, 6.60, 0,s}; Point(8) = {2.70, 6.60, 0,s};
Point(9) = {2.70, 0.00, 0,s}; Point(10) = {7.10, 0, 0,s};
Point(11) = {7.10, 5.75, 0,s}; Point(12) = {8.00, 5.75, 0,s};
Point(13) = {8.00, 0, 0,s}; Point(14) = {9.35, 0, 0,s};
Point(15) = {9.35, 9.30, 0,s};
Point(16) = {8.00, 9.30, 0,s}; Point(17) = {7.55, 7.10, 0,s};
Point(18) = {7.10, 9.30, 0,s}; Point(19) = {5.80, 9.30, 0,s};
Point(20) = {5.80, 2.15, 0,s}; Point(21) = {4.00, 2.15, 0,s};
Point(22) = {4.90, 3.05, 0,s}; Point(23) = {4.90, 4.80, 0,s};
Point(24) = {4.00, 5.75, 0,s}; Point(25) = {4.00, 6.60, 0,s};
Point(26) = {5.30, 6.60, 0,s}; Point(27) = {5.30, 9.30, 0,s};
Point(28) = {0, 9.30, 0,s};
Line(1) = {1,2}; Line(2) = {2,3}; Line(3) = {3,4};
Line(4) = {4,5}; Line(5) = {5,6}; Line(6) = {6,7};
Line(7) = {7,8}; Line(8) = {8,9}; Line(9) = {9,10};
Line(10) = {10,11}; Line(11) = {11,12}; Line(12) = {12,13};
Line(13) = {13,14}; Line(14) = {14,15}; Line(15) = {15,16};
Line(16) = {16,17}; Line(17) = {17,18}; Line(18) = {18,19};
Line(19) = {19,20}; Line(20) = {20,21}; Line(21) = {21,22};
Line(22) = {22,23}; Line(23) = {23,24}; Line(24) = {24,25};
Line(25) = {25,26}; Line(26) = {26,27}; Line(27) = {27,28};
Line(28) = {28,1};
Line Loop(1) = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28};
Plane Surface(111) = {1};
Physical Surface(222) = {111};
谢谢更新!
多谢!
您好 请问您了解pygmsh支持导入模型文件的网格划分吗
可以查看pygmsh的文档https://github.com/nschloe/pygmsh, 好像没有这个功能. 具体可以问下原作者, 谢谢!