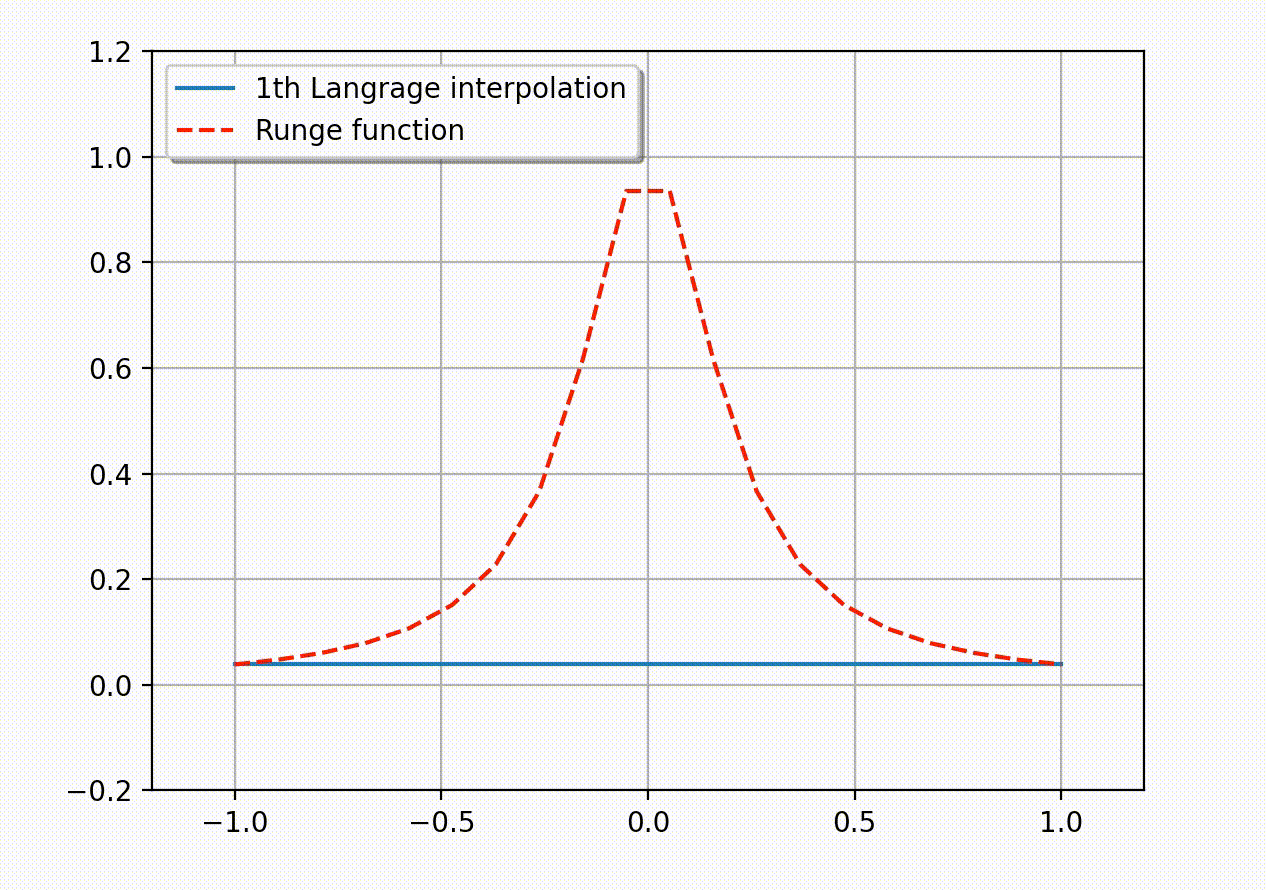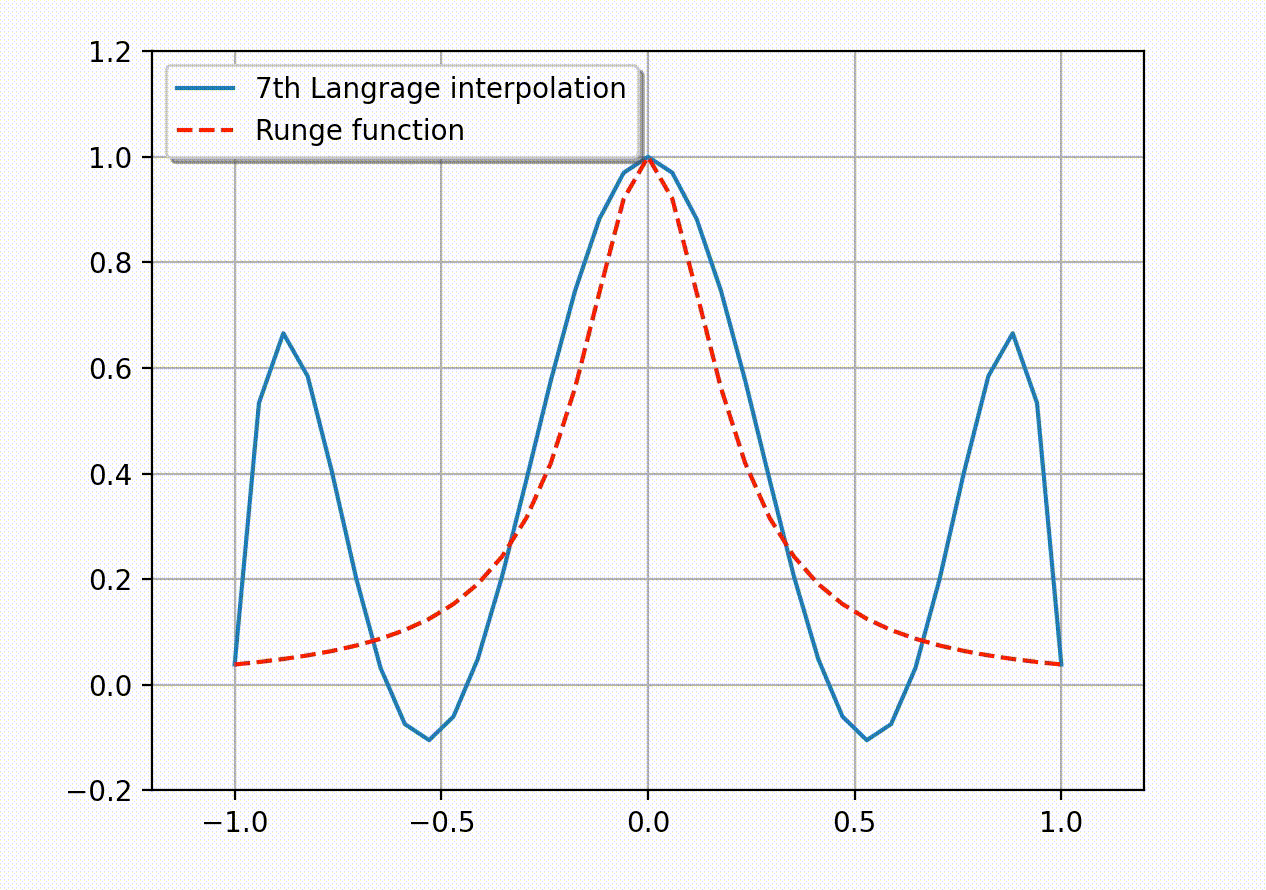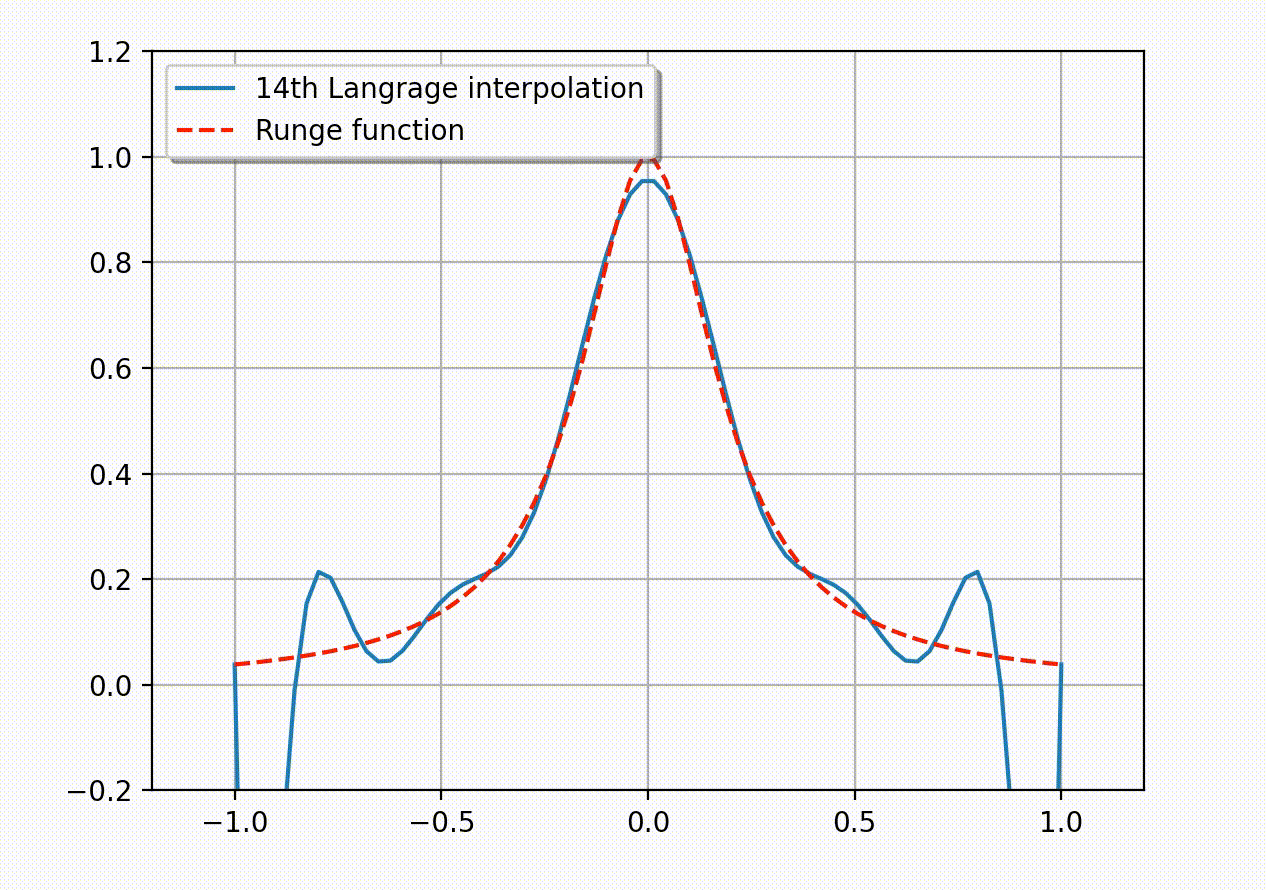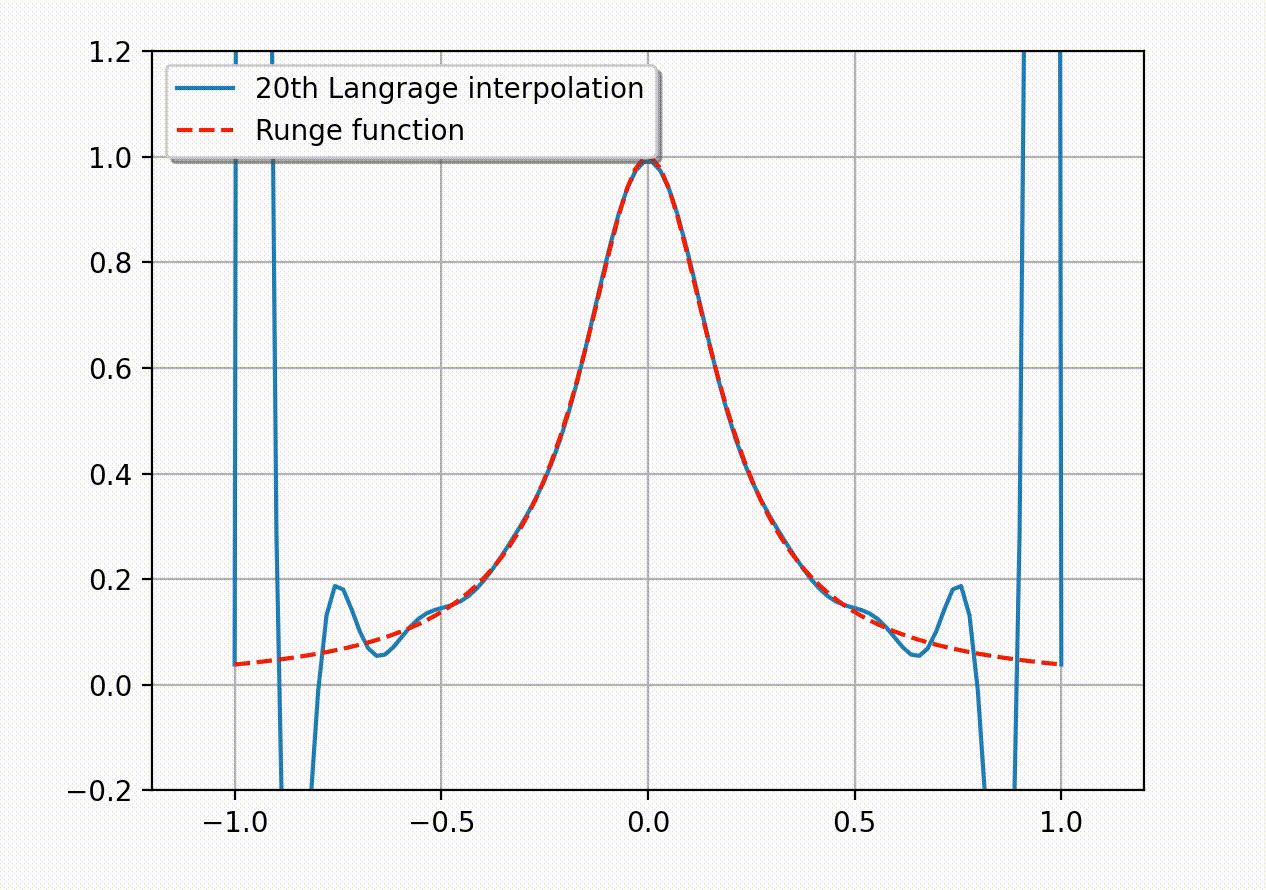
常用的等价无穷小

等价无穷小替换定理在求极限时经常会用到, 它可以简化求解过程.

定理(等价无穷小替换). 设 \(\alpha\) 和 \(\beta\) 是同一个变化过程中的无穷小量, 且 \(\alpha \sim \alpha^*\) 和 \(\beta \sim \beta^ *\). 若 \(\lim \frac{\beta^ *}{\alpha^*}\) 存在或为无穷大, 则\[ \lim \frac{\beta}{\alpha}=\lim \frac{\beta^ *}{\alpha^*}.\]

常用的等价无穷小:

\[ \begin{align*} \sin x &\sim x \quad (x \to 0) \\ \tan x &\sim x \quad (x \to 0) \\ \arcsin x &\sim x \quad (x \to 0) \\ \arctan x &\sim x \quad (x \to 0) \\ 1-\cos x &\sim \frac{1}{2}x^2 \quad ( x \to 0)\\ \sqrt[n]{1+x}-1 &\sim \frac{1}{n}x \quad (x \to 0)\\ (1+x)^n-1 &\sim nx \quad (x \to 0)\\ \ln (1+x) &\sim x \quad (x \to 0)\\ \log_a (1+x) & \sim \frac{x}{\ln a} \quad (x \to 0)\\ e^x-1 &\sim x \quad (x \to 0)\\ a^x-1 &\sim x \ln a \quad (x \to 0)\\\end{align*}\]

更多的例子:\[ \begin{align*} \tan x-\sin x &\sim \frac{1}{2} x^3 \quad (x \to 0)\\ x-\sin x &\sim \frac{1}{6} x^3 \quad (x \to 0)\\ \tan x-x &\sim \frac{1}{3} x^3 \quad (x \to 0)\\ \arctan x-\arcsin x &\sim -\frac{1}{2} x^3 \quad (x \to 0)\\ x-\arcsin x &\sim -\frac{1}{6} x^3 \quad (x \to 0)\\ \arctan x-x &\sim -\frac{1}{3} x^3 \quad (x \to 0)\\ \end{align*}\]

一些证明:
\[ \lim_{x \to 0} \frac{\ln (1+x)}{x} =\lim_{x \to 0} \ln (1+x)^{1/x} =\ln e = 1.\]\[ \lim_{x \to 0} \frac{e^x-1}{x} =\lim_{t \to 0} \frac{t}{\ln (1+t)} = 1 \quad (t:=e^x-1).\]\[ \lim_{x \to 0} \frac{\tan x-\sin x}{\frac{1}{2} x^3} =\lim_{x \to 0} \frac{\tan x(1-\cos x)}{\frac{1}{2} x^3} = 1.\]\[ \lim_{x \to 0} \frac{x-\sin x}{x^3} =\lim_{x \to 0} \frac{1-\cos x}{\frac{1}{3} x^2} = \frac{1}{6}.\]\[ \lim_{x \to 0} \frac{x-\arcsin x}{x^3} =\lim_{t \to 0} \frac{-(t-\sin t)}{\sin^3 t} =\lim_{t \to 0} \frac{-\frac{1}{6}t^3}{t^3} = -\frac{1}{6}.\]

一些示例:

\[ \begin{align*} (1) \lim_{x \to 0} \frac{\sqrt[]{1+\tan x}-\sqrt[]{1+\sin x}}{\sqrt[]{1+x \sin ^2x}-1} &=\lim_{x \to 0} \frac{\tan x-\sin x}{\sqrt[]{1+x \sin ^2x}-1}\frac{1}{\sqrt[]{1+\tan x}+\sqrt[]{1+\sin x}}\\ &=\lim_{x \to 0} \frac{\frac{1}{2}x^3}{\frac{1}{2}x \sin ^2x}\frac{1}{\sqrt[]{1+\tan x}+\sqrt[]{1+\sin x}}=\frac{1}{2}. \end{align*}\]
\[ \begin{align*} (2) \lim_{x \to 0} \frac{\sqrt[]{1+2x^2}-\cos x}{e^{x^2}-1} =\lim_{x \to 0} \frac{\sqrt[]{1+2x^2}-1}{e^{x^2}-1} +\lim_{x \to 0} \frac{1-\cos x}{e^{x^2}-1} = \frac{3}{2}. \end{align*}\]\[ \begin{align*} (3) \lim_{x \to 0} \frac{1}{x^3}\left[ \left( \frac{2+\cos x}{3} \right)^x-1 \right] &= \lim_{x \to 0} \frac{1}{x^3}\left[ e^{x\ln \left(1+ \frac{\cos x-1}{3} \right)}-1 \right]\\ &= \lim_{x \to 0} \frac{x\ln \left(1+ \frac{\cos x-1}{3} \right)}{x^3}\\ &= \lim_{x \to 0} \frac{ \frac{\cos x-1}{3}}{x^2}\\ &= \lim_{x \to 0} -\frac{1}{2}\frac{ x^2}{3x^2}=-\frac{1}{6}. \end{align*}\]
\[ \begin{align*} (4) &\lim_{x \to 0} \frac{1-\cos x \cdot \sqrt[]{\cos 2x} \cdot \sqrt[3]{\cos 3x}\cdots \sqrt[n]{\cos nx}}{x^2}\\ =&\lim_{x \to 0} -\frac{\cos x \cdot \sqrt[]{\cos 2x}\cdot \sqrt[3]{\cos 3x}\cdots \sqrt[n]{\cos nx}-1}{x^2}\\ =&\lim_{x \to 0} – \frac{\ln\cos x \cdot \sqrt[]{\cos 2x}\cdot \sqrt[3]{\cos 3x}\cdots \sqrt[n]{\cos nx}}{x^2}\\ =&\lim_{x \to 0} – \frac{\ln\cos x+\ln \sqrt[]{\cos 2x}+ \ln \sqrt[3]{\cos 3x}+\cdots+ \ln \sqrt[n]{\cos nx}}{x^2}\\ =&\lim_{x \to 0} \frac{1-\cos x}{x^2}+ \frac{1}{2}\frac{1-\cos 2x}{x^2}+\cdots +\frac{1}{n}\frac{1-\cos nx}{x^2}\\ =&\lim_{x \to 0} \frac{1}{2}+ \frac{1}{2}\frac{\frac{1}{2}(2x)^2}{x^2}+\cdots +\frac{1}{n}\frac{\frac{1}{2}(nx)^2}{x^2}\\ =&\lim_{x \to 0} \frac{1}{2}+ \frac{1}{2}\cdot 2+\cdots +\frac{1}{2}\cdot n = \frac{n(n-1)}{4}. \end{align*}\]