常微分方程初值问题: 若干数学模型
常微分方程初值问题又称为柯西问题, 在物理、化学、金融、社会科学等领域具有重要应用. 本文基于不同的应用场景, 列出了若干典型的数学模型.
目录
自由落体运动
如果一个石块或铁块从高处做自由落体运动, 比如著名的伽利略在比萨斜塔做的实验, 我们可以将石块或铁块看作一个质点, 从而忽略空气阻力, 其下降距离 \(y\) 关于时间 \(t\) 可以由一个二阶常微分方程来刻画. 初始时间 \(t=0\) 时, 位移为零, 即 \(y(0)=0\); 同时初始速度为零, 即 \(v(0)=y^{\prime}(0)=0\); 因为质点下降过程中只受到重力, 由牛顿第二定律可知 $$ m a = F_g = mg, $$ 这里 \(g=9.8\ m/s^2\) 表示重力加速度. 将加速度 \(a=y^{\prime\prime}(t)\) 代入上式即可得到一个二阶常微分方程 $$ y^{\prime\prime}(t) = g . \tag{Eq 1} $$ 通过结合初始条件 \(y(0)=0, y^{\prime}(0)=0\) 就构成了一个完整的初值问题. 可以验证上述问题的解就是我们非常熟悉的自由落体定律: $$ y(t) = \frac{1}{2}g t^2. $$
跳伞问题
不同于质点自由落体运动, 跳伞问题中不能忽略空气阻力的影响. 假设空气阻力与速度的平方成正比 (\(F_{air}=bv^2\)), 这里我们考虑下降位移 \(y(t)\) 关于时间的关系. 由牛顿第二定律可得如下方程 $$ m y^{\prime\prime} = m g – bv^2. $$ 其中负号是因为阻力方向与位移方向相反. 如果质量 \(m=1\), 并且假设初始位移 \(y(0)=0\), 初始速度为 \(v(0)=10\ m/s^2\), 我们就得到如下初值问题 $$ \begin{cases} y^{\prime\prime} = – b y^{\prime 2} + g , \\ y(0)=0, \ y^\prime(0)=10. \end{cases} \tag{Eq 2} $$
RLC 电路问题
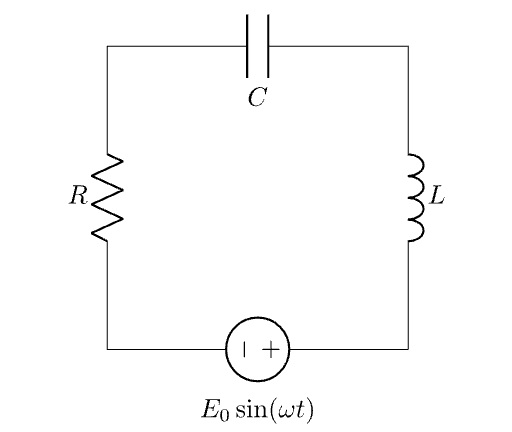
首先, 我们需要明确如下三个概念:
| 名称 | 定义 | 压降 |
| 电阻 | 电压与电流的比值: \(R=U/I\) | \(IR \) |
| 电容 | 电容器所带电量与两极间的电压的比值: \(C = Q/U\) | \(Q/C\) |
| 电感(自感) | 感生电动势与电流变化率的比值: \(L = U/(\frac{dI}{dt})\) | \(L\frac{dI}{dt}\) |
由 KVL (Kirchhoff’s Voltage Law) 可知, 总的电动势等于依次经过电阻, 电感和电容的压降之和, 因此我们可以得到 $$ IR + Q/C + L\frac{dI}{dt} = E(t). $$ 通过电容的电流和电量之间的关系为: \(I(t) = \frac{dQ(t)}{dt}\), 因此 $$ Q(t) = Q(0) + \int_0^t I(s) ds. $$ 利用上式中 \(Q(t)\) 的表达式可以得到 $$ IR + \frac{1}{C} \left( Q(0) + \int_0^t I(s) ds \right) + L\frac{dI}{dt} = E(t). \tag{Eq 3} $$ 将上式两边对时间求导, 即可得到电路中电流满足的二阶微分方程 $$ LI^{\prime\prime}(t) + R I^\prime(t) + \frac{1}{C}I(t) = E^\prime(t). \tag{Eq 4} $$
初始条件. 通常我们假设电路中的初始电流 \(I(0)=0\) 并且初始电容 \(Q(0)=0\), 由这两个条件和已知的电压 \(E(t)\) 就可以唯一确定方程 (Eq 4) 的解. 事实上, \(Q(0)=0\) 表明了另外一个初始值, 即初始电流变化率, 也就是说, 当 \(t=0\) 时, 方程 (Eq 3) 表明 $$ RI(0)+LI^\prime(0)=E(0) \Longrightarrow I^\prime(0)=(E(0)-RI(0))/L \Longrightarrow I^\prime(0)=E(0)/L. $$ 上式表明, 如果初始电流和电容为零, 那么电路中的初始电流变化率只依赖于初始电压; 如果初始电压为零, 那么初始电流变化率同样为零. 这个结果实际上就是由 KVL 导出的.
单摆运动

由杆连接的球的摆动可以由一个二阶微分方程来刻画. 具体的, 假设杆的长度为 \(L\), 球的质量为 \(m\), \(\theta\) 表示角度偏量 (逆时针为正向). 重力沿运动方程的分量为 \(mg\sin\theta\), 球体的加速度为 \((L\theta)^{\prime\prime}\), 那么牛顿第二定律表明任意时刻这两个力都是平衡的 (注意两个力的方向始终都是相反的): $$ m L\theta^{\prime\prime} + mg\sin\theta =0, $$ 也就得到了如下的二阶非线性方程 $$ \theta^{\prime\prime} + \frac{g}{L}\sin\theta =0. \tag{Eq. 5a} $$ 当角度 \(\theta\) 比较小时, 我们可以利用 \(\theta\approx \sin\theta\) 得到简化的线性方程 $$ \theta^{\prime\prime} + \frac{g}{L}\theta =0. \tag{Eq. 5b} $$ 上面的线性方程可以很容易的得到解析解. 当角度 \(\theta\) 比较大时, 上面的近似方程就不能用来准确刻画单摆的运动了, 必须寻求数值方法来求解方程 (Eq. 5a).
弹簧振动
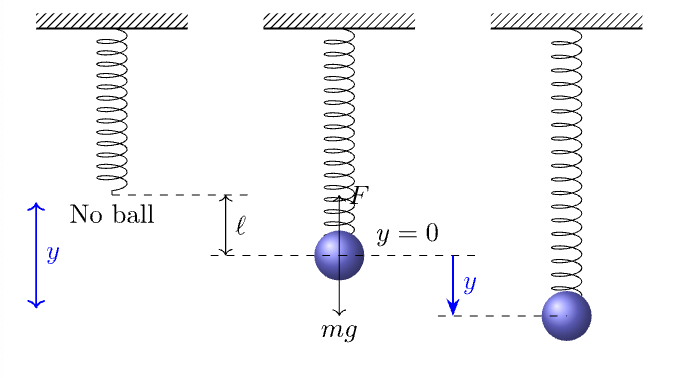
考虑球体在弹簧作用下的无阻尼振动情况. 如果我们将球体从平衡位置向下拉动一段距离, 那么位移为正, 这样就使弹簧产生一个反向拉力 \(F_1=-ky\), 然后由牛顿第二定律可得 $$ m y^{\prime\prime} + ky = 0. \tag{Eq. 6a} $$ 如果在球体的下方连接一个缓冲器, 作为振动的阻力, 一般与速度的平方成正比, 方向与运动方向相反, \(F_2=-cy^\prime\), 那么上面的方程就为阻尼振动方程 $$ m y^{\prime\prime} + cy^\prime + ky = 0. \tag{Eq. 6b} $$
捕食者-猎物种群模型
捕食者-猎物种群模型 (Predator–Prey Population Model) 也被称为 Lotka-Volterra 方程, 是一对一阶非线性微分方程, 经常用于描述生物系统中两个物种相互作用的动力学过程, 一个作为捕食者, 另一个作为猎物. 模型假设(以狐狸和兔子的捕食关系为例):
- 兔子拥有充足的食物. 那么, 如果没有狐狸, 兔子的数量 \(y_1(t)\) 满足 \(y_1^{\prime} = ay_1,\ a>0\).
- 兔子的减少速度正比于兔子和狐狸数量的乘积, 也就是说 \(y_1^{\prime} = ay_1-by_1y_2\), 其中 \(y_2\) 表示狐狸的种群数量, \(b>0\).
- 如果没有兔子, 狐狸的数量将会指数减少, \(y_2^{\prime}=-l y_2\); 狐狸数目的增加速度还与两者相遇的次数成正比, \(y_2^{\prime}=ky_1y_2-l y_2 , \ l>0\).
综合以上假设, 我们可以得到 Lotka-Volterra 方程组 $$ \begin{align*} y_1^{\prime} &= ay_1-by_1y_2,\\ y_2^{\prime} &= ky_1y_2-l y_2 . \end{align*} $$
SIR 传染病模型
SIR 传染病模型是常微分方程应用中最经典的模型之一. 首先, 我们需要三个变量来刻画三类不同的人群:
- \(S=S(t)\) 为易感人群数目 (Susceptible individuals);
- \(I=I(t)\) 为已感染人群数目 (Infected individuals);
- \(R=R(t)\) 为恢复人群数目 (Recovered individuals).
通常为简化模型, 我们以它们在总人口的比例为变量来描述微分方程, \(s=S(t), i=I(t), r=R(t)\). 假设:
- 总的人口数量不变, 忽略人口自然死亡或者移民等因素, 即 \(s(t)+i(t)+r(t)=1\).
- 所有个体都属于上述三类人群之一 可以从易感人群因感染疾病进入到已感染人群, 而后进入已恢复人群. 感染数目, 也就是易感人群的减少速度与两类人群的接触成正比, 即 \(\beta s(t)i(t)\), 其中 \(\beta\) 为正比系数.
- 假设恢复速度与已感染人群数量成正比, 比率为 \(k\). 例如, 如果感染个体平均需要 3 天来恢复, 那么每天就会有三分之一的感染人群从疾病中恢复.
利用上面的假设条件, 我们可以得到如下的微分方程 $$ \begin{align*} \frac{ds}{dt} &= – \beta s(t) i(t), && \text{易感方程} \\ \frac{dr}{dt} &= k i(t),&& \text{恢复方程}\\ \frac{di}{dt} &= \frac{d}{dt} (1-s-t)= \beta s(t) i(t) – ki(t), && \text{感染方程} \end{align*} $$
一个简单的实例是 20 世纪 60 年代香港流感在纽约的传播过程. 如果假设最开始有 10 个感染个体通过旅行到达纽约, 并且最开始的时候当地 7,900,000 个个体没有任何感染, 那么初始条件就是 $$ s(t) = 1,\quad i(t) = 10/7900000\approx 1.27e-6,\quad r(0)=0. $$ 如果令其中的参数 \(\beta=1/2, k=1/3\), 那么通过求解上述方程, 可以得到如下不同人群数量的变化情况.
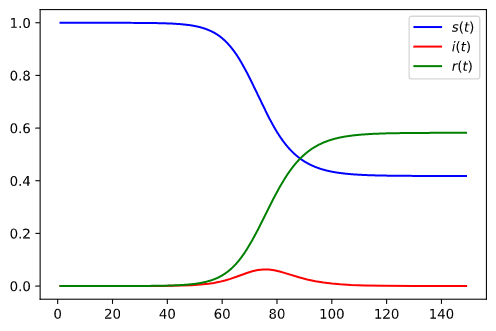
附录 A. SIR 模型的 Python 代码
# SIR model: b=.5, k=1/3
# s'=-bsi, s(0) = 1
# i'=bsi-ki, i(0) = 1.27e-6
# r'=ki, r(0) = 0
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# Define derivative function
def f(t, y, b, k):
dydt = [-b*y[0]*y[1], b*y[0]*y[1]-k*y[1], k*y[1]]
return dydt
# Define time spans, initial values, and constants
tspan = np.arange(1, 150)
yinit = [1., 1.27e-6, 0.]
b, k = .5, 1./3
# Solve differential equation
sol = solve_ivp(f, [tspan[0], tspan[-1]], yinit, args=(b, k), t_eval=tspan)
# Plot states
fig, ax = plt.subplots()
ax.plot(sol.t, sol.y[0],'-b')
ax.plot(sol.t, sol.y[1],'-r')
ax.plot(sol.t, sol.y[2],'-g')
ax.legend(['$s(t)$','$i(t)$','$r(t)$'])
plt.show()
参考文献
- Kreyszig, E. (2011). Advanced Engineering Mathematics. (10th ed.).
- D. Smith and L. Moore. The SIR Model for Spread of Disease. Mathematical Association of America.
好资料